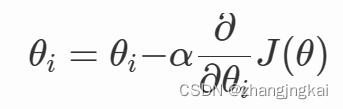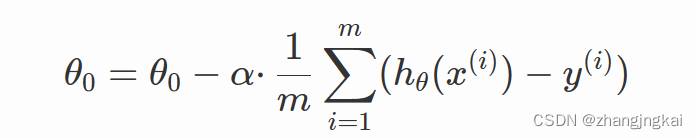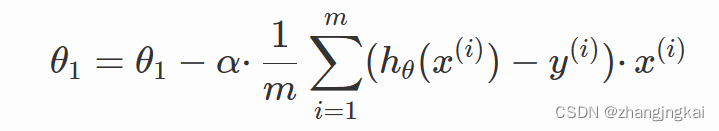机器学习

您所在的位置：网站首页 › 最值问题的常用类型 › 机器学习

机器学习

2023-07-07 17:03| 来源: 网络整理| 查看: 265

一、线性回归

1.什么是线性回归

2.一般形式的线性回归模型

3.最小二乘法求解参数

4.最小二乘法推演过程

二、梯度下降算法

1.什么是梯度下降算法

2.核心公式

3.基本步骤

4.常用的三种类型

1.批量梯度下降法（Batch Gradient Descent）

2.随机梯度下降法（Stochastic Gradient Descent）

3.小批量梯度下降法（Mini-batch Gradient Descent）

三.一元线性回归的推演过程

四、代码实现

总结

一、线性回归 1.什么是线性回归

线性回归（Linear Regression）是一种用于建立连续变量之间线性关系的统计模型。它假设目标变量与自变量之间存在线性关系，并试图通过拟合一条最佳的直线或超平面来预测目标变量的值。

2.一般形式的线性回归模型

$h_\theta \left ( x \right )=\theta_0x_0+\theta_1x_1+\theta_2x_2+\cdots +\theta_nx_n+\varepsilon$

其中，hθ(x)是因变量，x0,x1, x2, ..., xn是自变量，θ0, θ1, θ2, ..., θn是回归系数（也称为权重或斜率），ε是误差项。回归系数θ0, θ1, θ2, ..., θn表示了自变量对因变量的影响，它们衡量了自变量在单位变动时对因变量的变化量。误差项ε代表了模型无法完全解释的变异性，它是由于其他未观测到的因素或随机误差引起的。

优化目标：线性回归的目标是寻找最佳拟合线，使预测值与实际值之间的误差最小化。通常使用最小二乘法作为优化目标，即最小化预测值与实际值之间的平方差。

3.最小二乘法求解参数

最小二乘法就是使估计值与实际值差距最小的一种方法。

它的目标是最小化残差平方和，即预测值与实际值之间的差的平方和。通过最小化残差平方和，可以得到最佳拟合线的参数估计值。最小二乘法的参数估计公式可以使用矩阵形式表示：

$\theta =(X^TX)^{-1}X^Ty$

其中θ是参数向量，X是自变量矩阵，y是目标变量向量。^(-1)表示矩阵的逆运算。

4.最小二乘法推演过程

$h_\theta \left ( x \right )=\theta_0x_0+\theta_1x_1+\theta_2x_2+\cdots +\theta_nx_n+\varepsilon$

由拟合的线性回归模型进行整合得到： $h_\theta \left ( x \right )=\sum_{i=0}^{n}\theta _ix=\theta ^Tx^{(i)}$

因为其为拟合的数据（预测值），与实际值（真实值）存在误差，可以得到： $y^{(i)}=\theta ^Tx^{(i)}+\varepsilon ^{(i)}$

其中 $\varepsilon$ 为误差，误差 $\varepsilon ^{(i)}$ 是独立并且具有相同的分布，并且服从均值为0方差为 $\theta ^2$ 的高斯分布

为使预测值更接近于真实值，就要使误差尽可能的小

由于误差服从高斯分布： $p(\varepsilon ^{(i)})=\frac {1}{\sqrt{2\pi }\sigma }exp(-\frac{(\varepsilon ^{(i)})^2}{2\sigma ^2})$

将误差用真实值和预测值表示 $\varepsilon ^{(i)}=y^{(i)}-\theta ^Tx^{(i)}$

而对于拟合的线性回归来说，数据越多，越准确。代入大量参数可得：

$L(\theta )=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)},\theta )=\prod_{i=1}^{m}\frac {1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-\theta ^Tx^{(i)})^2}{2\sigma ^2})$

为方便计算，可以加log函数使累乘变为累加 $logL(\theta )=log\prod_{i=1}^{m}\frac {1}{\sqrt{2\pi }\sigma }exp(-\frac{(y^{(i)}-\theta ^Tx^{(i)})^2}{2\sigma ^2})$

又式子中有exp，使log底数为e，化简得： $lnL(\theta )=mln\frac {1}{\sqrt{2\pi }\sigma }-\frac{1}{\sigma ^2}*\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta ^Tx^{(i)})^2$

这是由误差经高斯函数化来的误差的概率，又其服从均值为0的分布，故使其越大，误差就越接近0

为了让这个式子越大，只能使 $\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta ^Tx^{(i)})^2$ 越小

使 $J(\theta )=\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta ^Tx^{(i)})^2$

目标函数可化为： $J(\theta )=\frac{1}{2}\sum_{i=1}^{m}(\theta ^Tx^{(i)}-y^{(i)})^2=\frac{1}{2}(X\theta -y)^T(X\theta -y)$

当对θ的偏导为0时，函数最小

对θ求偏导且使其为0可得： $\theta =(X^TX)^{-1}X^Ty$

二、梯度下降算法 1.什么是梯度下降算法

梯度下降是迭代法的一种,在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降是最常采用的方法之一。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。

梯度下降法(gradient descent)是一个最优化算法，常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。

特点：越接近目标值，步长越小，下降速度越慢

2.核心公式

其中ɑ为学习率，也是梯度下降的步长，决定了每次迭代参数更新的幅度。

∂/∂θiJ(θ)为梯度，梯度指示了参数更新的方向。

3.基本步骤

初始化参数：选择合适的初始参数 θi，可以是随机选择或根据已知条件进行选择。

计算梯度：计算目标函数在当前参数值 θi处的梯度 ∂/∂θiJ(θ)。

更新参数：根据梯度和学习率，使用梯度下降公式更新参数，得到新的参数值 θi。

判断停止条件：判断是否达到停止条件，例如目标函数的值变化已经很小或迭代次数已经达到预设值。

如果停止条件未满足，回到步骤2，继续迭代更新参数。

4.常用的三种类型 1.批量梯度下降法（Batch Gradient Descent）

在每个迭代步骤中使用所有训练样本来更新模型参数，用来找到全局最优解（如果存在）。

优点：可以全局优化。

缺点：可能会陷入局部最优解，在大规模数据集上的计算代价较高，学习过程较慢。

2.随机梯度下降法（Stochastic Gradient Descent）

每次迭代只使用一个样本，它能够逐渐接近真实的梯度，从而在一些情况下可以更快地找到最优解。

优点：计算开销较小，特别适用于大规模数据集。

缺点：存在较大的随机性，可能会出现震荡现象。只使用一个样本计算梯度，可能会导致噪声较大的梯度估计，从而影响收敛速度和最终的解的质量。

3.小批量梯度下降法（Mini-batch Gradient Descent）

使用一个介于一个样本和整个训练集之间的小批量样本来更新模型参数。

优点：相对于批量梯度下降法来说，占用的计算资源更少，并且收敛速度更快。相对于随机梯度下降法来说，更稳定且减少了梯度估计的噪声。

缺点：引入了一个新的超参数——小批量大小，需要进行调优，并且由于每个小批量样本数量并没有达到整个训练集的数量，因此可能会降低对全局优化的准确性。

三.一元线性回归的推演过程

设线性回归函数为:

利用梯度下降法来实现对线性回归函数的推导运算，为使得误差最小，需要代价函数最小，代价函数：

对代价函数进行求偏导得到θ0和θ1：

若是得到损失函数的值要小于所设置的最小误差（一般为0.001），就是最终结果，若大于，则需要再次求导计算。

四、代码实现

按照步骤先确定初始值和学习率

theta0 = uniform(0,2) #对theta0进行初始赋值 theta1 = uniform(0,2) #对theta1进行初始赋值 learning_rate = 0.1 #学习率 m = len(x) #数据个数m count = 0 loss = []

求导（也是梯度）

for num in range(10000): count += 1 #记录迭代次数 diss = 0 #误差 der0 = 0 #对theata0的偏导数 der1 = 0 #对theata1偏导数 #求导 for i in range(m): der0 += (theta0+theta1*x[i]-y[i])/m der1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]

更新参数

for i in range(m): theta0 = theta0 - learning_rate*((theta0+theta1*x[i]-y[i])/m) theta1 = theta1 - learning_rate*((theta0+theta1*x[i]-y[i])/m)*x[i]

然后求误差函数来判断是否收敛

#求损失函数 J (θ) for i in range(m): diss = diss + (1/(2*m))*pow((theta0+theta1*x[i]-y[i]),2) loss. Append(diss) #如果误差已经很小，则退出循环 if diss

【本文地址】

机器学习

机器学习

今日新闻

推荐新闻