令人头疼的优化问题 |
您所在的位置:网站首页 › 最优点最优值和最优解 › 令人头疼的优化问题 |
令人头疼的优化问题
|
😽 今天我们要来解决一个运筹学中较为头疼的问题,多目标规划问题。 1.多目标规划问题的描述多目标问题可以描述成如下问题: 目前求解多目标优化问题方法算法主要有基于数学的规划方法和基于遗传算法的两类方法;其中带精英策略的快速非支配排序算法(NSGA-II)是影响最大和应用范围最广的一种多目标遗传算法。在其出现以后,由于它简单有效以及比较明显的优越性,使得该算法已经成为多目标优化问题中的基本算法之一,该算法主要优点: 提出了快速非支配的排序算法,降低了计算非支配序的复杂度。引入了精英策略,扩大了采样空间。将父代种群与其产生的子代种群组合在一起,共同通过竞争来产生下一代种群,这有利于是父代中的优良个体得以保持,保证那些优良的个体在进化过程中不被丢弃,从而提高优化结果的准确度。并且通过对种群所有个体分层存放,使得最佳个体不会丢失,能够迅速提高种群水平。引入拥挤度和拥挤度比较算子,这不但克服了NSGA算法中需要人为指定共享参数的缺陷,而且将拥挤度作为种群中个体之间的比较准则,使得准Pareto域中的种群个体能均匀扩展到整个Pareto域,从而保证了种群的多样性。 3.matlab求解Matlab中提供函数gamultiobj采用的算法就是基于NSGA-II改进的一种多目标优化算法(a variant of NSGA-II),接下来对目标规划中的一些概念进行介绍。 3.1 支配(dominate)与非劣(non-inferior)在多目标规划问题中,如果个体p至少有一个目标比个体q的好,而且个体p的所有目标都不比个体q的差,那么称个体p支配个体q(p dominate q),或者称个体q受个体p支配(q is dominated by p),也可以说,个体p非劣个体q(p is non- inferior to q)。 3.2 序值(rank)和前端(front)如果p支配q,那么p的序值比q低,如果p和q互不支配,或者说,p和q互相非劣,那么p和q有相同的序值,序值为1的个体属于第一前端,序值为2的个体属于第二前端,依此推类。显然,在当前种群中,第一前端是完全不受支配的,第二前端受第一前端中个体是支配,这样,通过排序,可以将种群中的个体分配到不同的前端。 3.3 拥挤距离(crowding-distance)拥挤距离用来计算某前端中的某个体与与该前端中其他个体之间的距离,用以表征个体间的拥挤程度。显然,拥挤距离的值越大,个体间就越不用拥挤,种群的多样性就越好。需要指出的是,只有处于同一前端的个体间才需要计算拥挤距离,不同前端之间计算距离是没有意义的。 3.4 最优前端个体系数(paretofraction)最优前端个体系数定义为最优前端中的个体在种群中所占有的比例,即最优前端个体数=min{paretofraction ∗ * ∗种群大小,前端中现存的个体数目},其取值范围为[0到1]。 4.案例求解如下问题的解: 解释一下gamultiobj里面的参数: [ x , f v a l ] = g a m u l t i o b j ( f i t n e s s f c n , n v a r s , A , b , A e q , b e d , l b , u b , o p t i o n s ) [x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,bed,lb,ub,options) [x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,bed,lb,ub,options) 其中x为函数gamultiobj得到的帕累托最优解集,fval为对应x目标函数;fitnessfcn为目标函数句柄,同函数ga一样,需要编写一个描述目标函数M的文件,navrs为变量数目;A、b、Aeq、bep为线性约束,可以表示为 A ∗ X < = B , A e q ∗ X = b e p A*X |
【本文地址】
今日新闻 |
推荐新闻 |
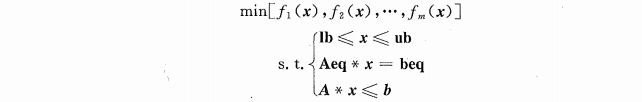 其中,
f
i
(
x
)
f_i(x)
fi(x)为待优化的目标函数;x为待优化的变量;lb和ub分别为变量x的下限和上限约束;Aeq
∗
*
∗x=beq为变量x的线性等式约束;A
∗
*
∗x
≤
\leq
≤b为变量x的线性不等式约束。
其中,
f
i
(
x
)
f_i(x)
fi(x)为待优化的目标函数;x为待优化的变量;lb和ub分别为变量x的下限和上限约束;Aeq
∗
*
∗x=beq为变量x的线性等式约束;A
∗
*
∗x
≤
\leq
≤b为变量x的线性不等式约束。 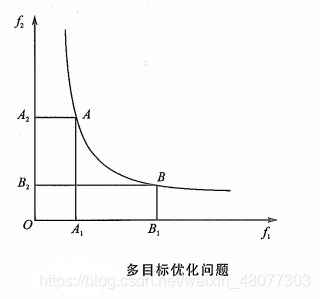 在该问题中,目标函数
f
1
f_1
f1和
f
2
f_2
f2是相互矛盾的。如上图,因为
A
1
<
B
1
A_1B_2
A2>B2也就是说,某一个目标函数的提高需要以另一个目标函数的降低作为代价,我们称这样的解A和B是非劣解,或者说是帕累托最优解,多目标规划问题就是要求解这些帕累托最优解。
在该问题中,目标函数
f
1
f_1
f1和
f
2
f_2
f2是相互矛盾的。如上图,因为
A
1
<
B
1
A_1B_2
A2>B2也就是说,某一个目标函数的提高需要以另一个目标函数的降低作为代价,我们称这样的解A和B是非劣解,或者说是帕累托最优解,多目标规划问题就是要求解这些帕累托最优解。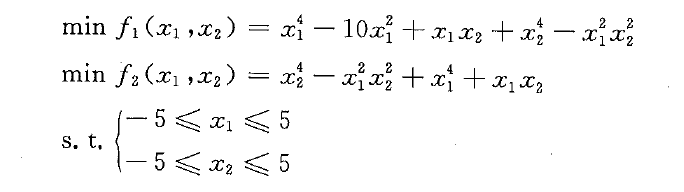 使用gamultiobj求解,主要分为两部分
使用gamultiobj求解,主要分为两部分