【运筹学】线性规划 图解法 ( 唯一最优解 |
您所在的位置：网站首页 › 最优解是一个值还是一个坐标 › 【运筹学】线性规划 图解法 ( 唯一最优解 |
【运筹学】线性规划 图解法 ( 唯一最优解
|
文章目录I . 图解法II. 图解法 处理 线性规划问题 ( 取最大值 仅有一个最优解的情况 )III . 图解法 处理 线性规划问题 ( 取最大值 有无穷多最优解 )IV . 图解法 处理 线性规划问题 ( 取最小值 有一个最优解 )V . 图解法 处理 线性规划问题 ( 无界解 )VI . 图解法 处理 线性规划问题 ( 无可行解 )VII . 线性规划解的情况I . 图解法 线性规划问题求解有两种方法 : ① 图解法 , ② 单纯形法 ; 1. 图解法 : 适用于 两个 或 三个 变量 , 如果是两个变量 , 需要绘制直角坐标系 , 如果是 三个变量 , 需要绘制立体坐标系 ;2. 单纯形法 : 适用于任意变量 , 但必须将线性规划数学模型转为标准形式 ;本篇只讨论 两个变量的 图解法 , 在直角坐标系中进行绘图 ; 图解法意义 : 1. 局限性大 : 实际情况下 , 我们都使用单纯形法求线性规划的解 , 图解法只能处理 2 到 3 个变量的线性规划问题 ;2. 优势 : 图解法 简单 , 直观 , 便于初期对线性规划问题的 原理 和 几何意义 进行深入理解 ;II. 图解法 处理 线性规划问题 ( 取最大值 仅有一个最优解的情况 )使用图解法解下面的线性规划问题 : \begin{array}{lcl} max Z = 2x_1 + x_2\\\\ s.t = \begin{cases} x_1 + 1.9x_2 \geq 3.8\\\\ x_1 - 1.9x_2 \leq 3.8\\\\ x_1 + 1.9x_2 \leq 10.2\\\\ x_1 - 1.9x_2 \geq -3.8\\\\ x_1 , x_2 \geq 0 \end{cases} \end{array}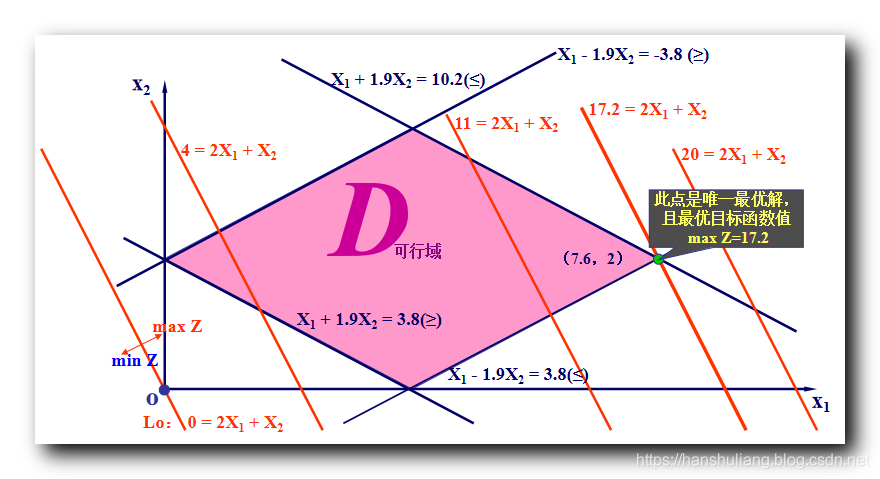 在这里插入图片描述大于等于 不等式 需要取直线 右侧区域 ; 小宇等于 不等式 需要取直线 左侧区域 ; 四条直线 形成一个 四边形区域 ; 绘制目标函数 , 使 2x_1 + x_2与 上述 四边形相交 , 取最大值 , 经过计算 , 得到的结果最大为 20, 此时 x_1 = 7.6 , x_2 = 2III . 图解法 处理 线性规划问题 ( 取最大值 有无穷多最优解 )使用图解法解下面的线性规划问题 : \begin{array}{lcl} max Z = 3x_1 + 5.7x_2\\\\ s.t = \begin{cases} x_1 + 1.9x_2 \geq 3.8\\\\ x_1 - 1.9x_2 \leq 3.8\\\\ x_1 + 1.9x_2 \leq 10.2\\\\ x_1 - 1.9x_2 \geq -3.8\\\\ x_1 , x_2 \geq 0 \end{cases} \end{array}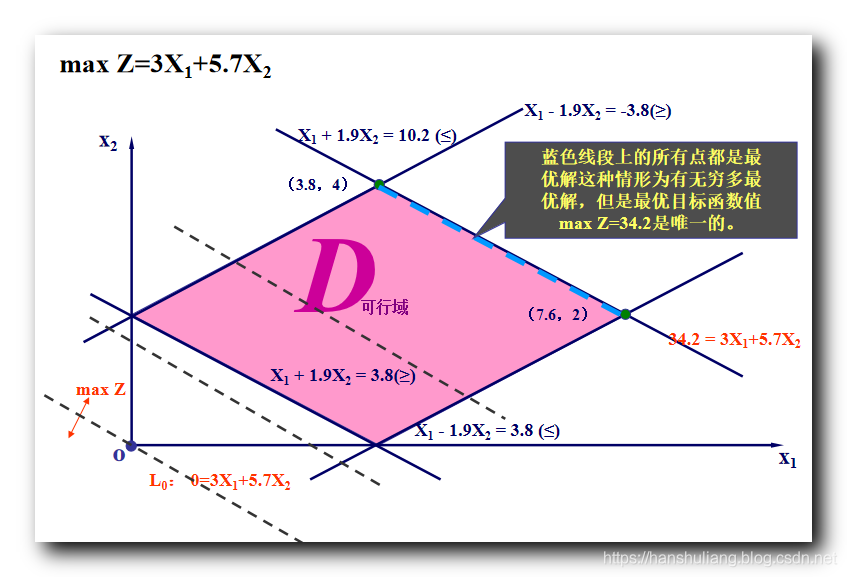 在这里插入图片描述大于等于 不等式 需要取直线 右侧区域 ; 小宇等于 不等式 需要取直线 左侧区域 ; 四条直线 形成一个 四边形区域 ; 绘制目标函数 , 使 3x_1 + 5.7x_2与 上述 四边形相交 , 取最大值 , 注意该函数 图像在 坐标系中 与 x_1 + 1.9x_2 = 10.2图像是平行的 , 即在可行区域内 , 整个线段上所有的点都是最优解 ; 这个最优解的个数是无穷多个 ; 经过计算 , 得到的结果最大为 34.2, 此时 ( 3.8 , 4 ) 到 ( 7.6 , 2 )线段之间的所有的点都是最优解 IV . 图解法 处理 线性规划问题 ( 取最小值 有一个最优解 )使用图解法解下面的线性规划问题 : \begin{array}{lcl} min Z = 5x_1 + 4x_2\\\\ s.t = \begin{cases} x_1 + 1.9x_2 \geq 3.8\\\\ x_1 - 1.9x_2 \leq 3.8\\\\ x_1 + 1.9x_2 \leq 10.2\\\\ x_1 - 1.9x_2 \geq -3.8\\\\ x_1 , x_2 \geq 0 \end{cases} \end{array}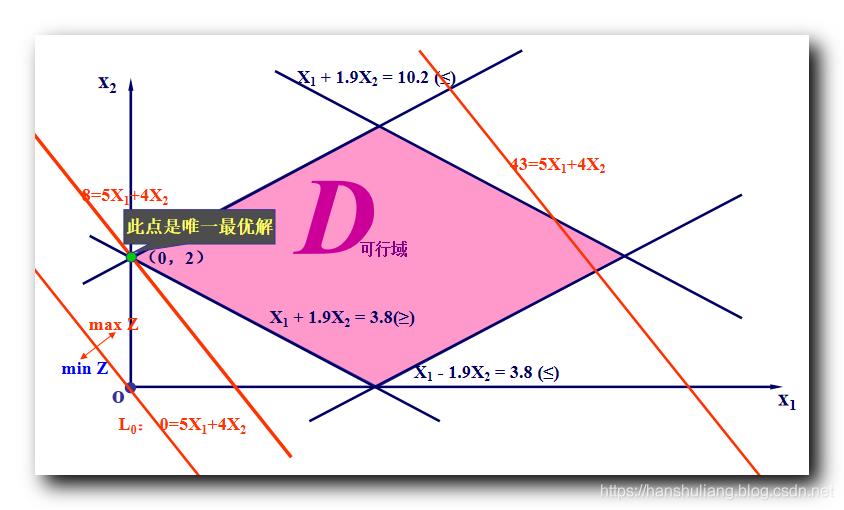 在这里插入图片描述大于等于 不等式 需要取直线 右侧区域 ; 小宇等于 不等式 需要取直线 左侧区域 ; 四条直线 形成一个 四边形区域 ; 绘制目标函数 , 使 5x_1 + 4x_2=0的 图像的 平行直线 与 上述 四边形相交 , 取最小值 , 经过计算 , 得到的结果最小值为 8, 此时 x_1 = 0 , x_2 = 2V . 图解法 处理 线性规划问题 ( 无界解 )使用图解法解下面的线性规划问题 : \begin{array}{lcl} max Z = x_1 + 2x_2\\\\ s.t = \begin{cases} x_1 + 3x_2 \geq 6\\\\ x_1 + x_2 \geq 4\\\\ 3x_1 + x_2 \geq 6\\\\ x_1 , x_2 \geq 0 \end{cases} \end{array}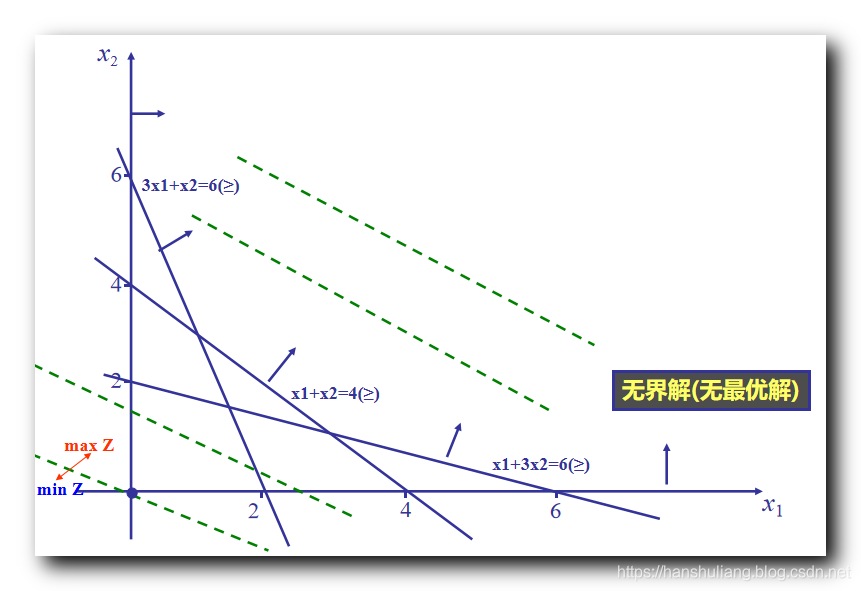 在这里插入图片描述大于等于 不等式 需要取直线 右侧区域 ; 小宇等于 不等式 需要取直线 左侧区域 ; 四条直线 无法 形成一个 闭合形区域 , 整体区域是开放的 , 最优解随着 x_1 , x_2变量增加而增大 , 没有任何限制 此时该线性规划有无数个解 , 并且其最大值没有边界 ; 这种情况下称为线性规划的解是无界解 , 同时也没有最优解 ; VI . 图解法 处理 线性规划问题 ( 无可行解 )使用图解法解下面的线性规划问题 : \begin{array}{lcl} max Z = 3x_1 + 4x_2\\\\ s.t = \begin{cases} 2x_1 + x_2 \leq 40\\\\ x_1 + 1.5x_2 \leq 30\\\\ x_1 + x_2 \geq 50\\\\ x_1 , x_2 \geq 0 \end{cases} \end{array}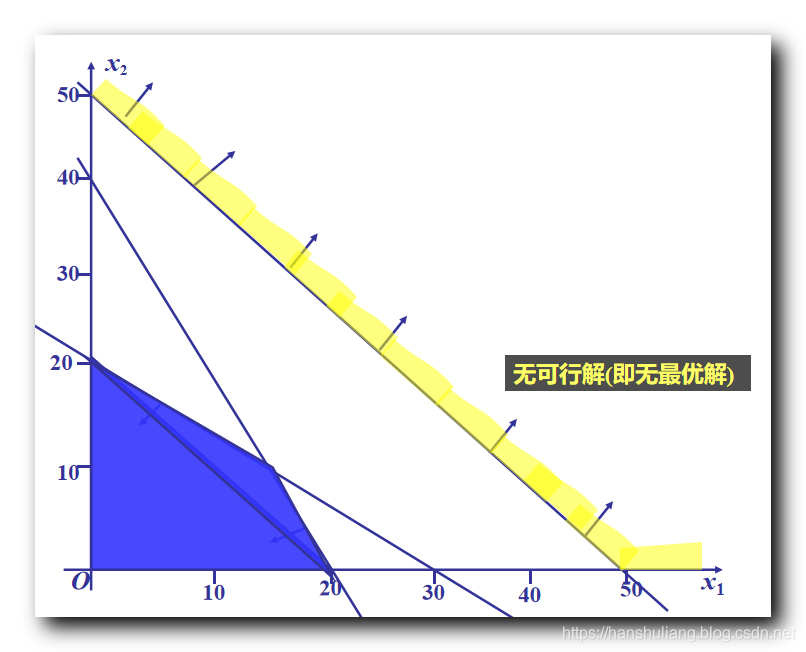 在这里插入图片描述大于等于 不等式 需要取直线 右侧区域 ; 小宇等于 不等式 需要取直线 左侧区域 ; 绘制目标函数 , 绘制 3x_1 + 4x_2 \geq 0的 图像 , 发现 该图像的 任何 平行直线 与 上述 四边形 都不相交 , 这种情况属于没有 可行解 , 同时也没有最优解 VII . 线性规划解的情况线性规划有以下情况的解 : ① 有唯一最优解 , ② 有无穷多最优解 , ③ 无界解 , ④ 无可行解 ; 使用图解法的关键 : ① 可行域 : 根据 大于等于 或 小宇等于 不等式 , 判断可行区域 ;② 目标函数绘制 : 目标函数的移动方向 , 其变量必须都大于 0 , 先绘制 等于 0 的直线 , 然后都必须朝着大于 0 的方向移动 ; |
【本文地址】