高中数学解析几何绝活一:极点极线的推导和应用 |
您所在的位置:网站首页 › 曲线的方程和方程的曲线的概念是什么 › 高中数学解析几何绝活一:极点极线的推导和应用 |
高中数学解析几何绝活一:极点极线的推导和应用
|
预备知识:
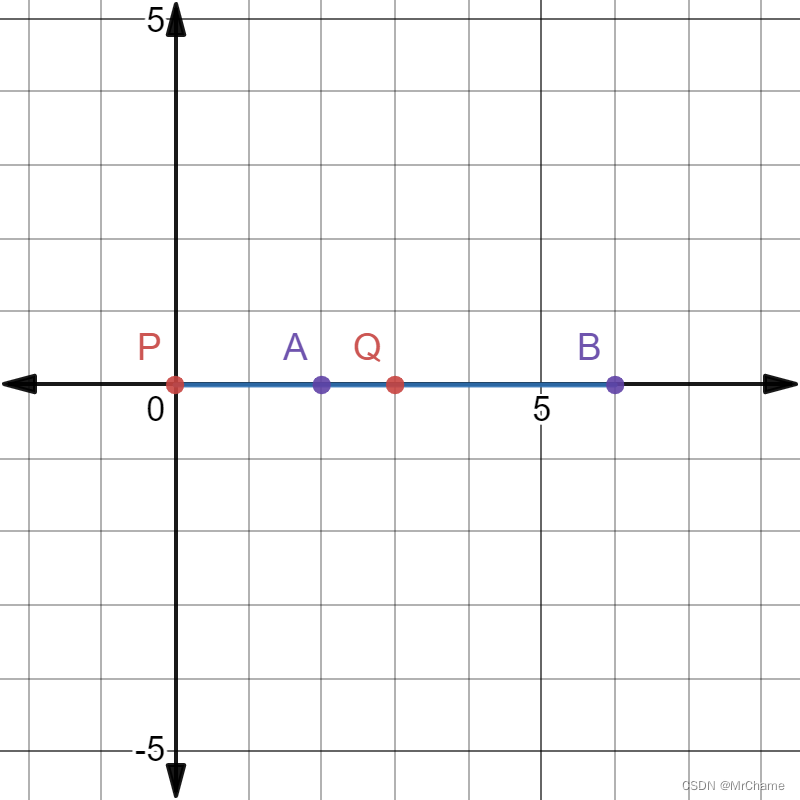
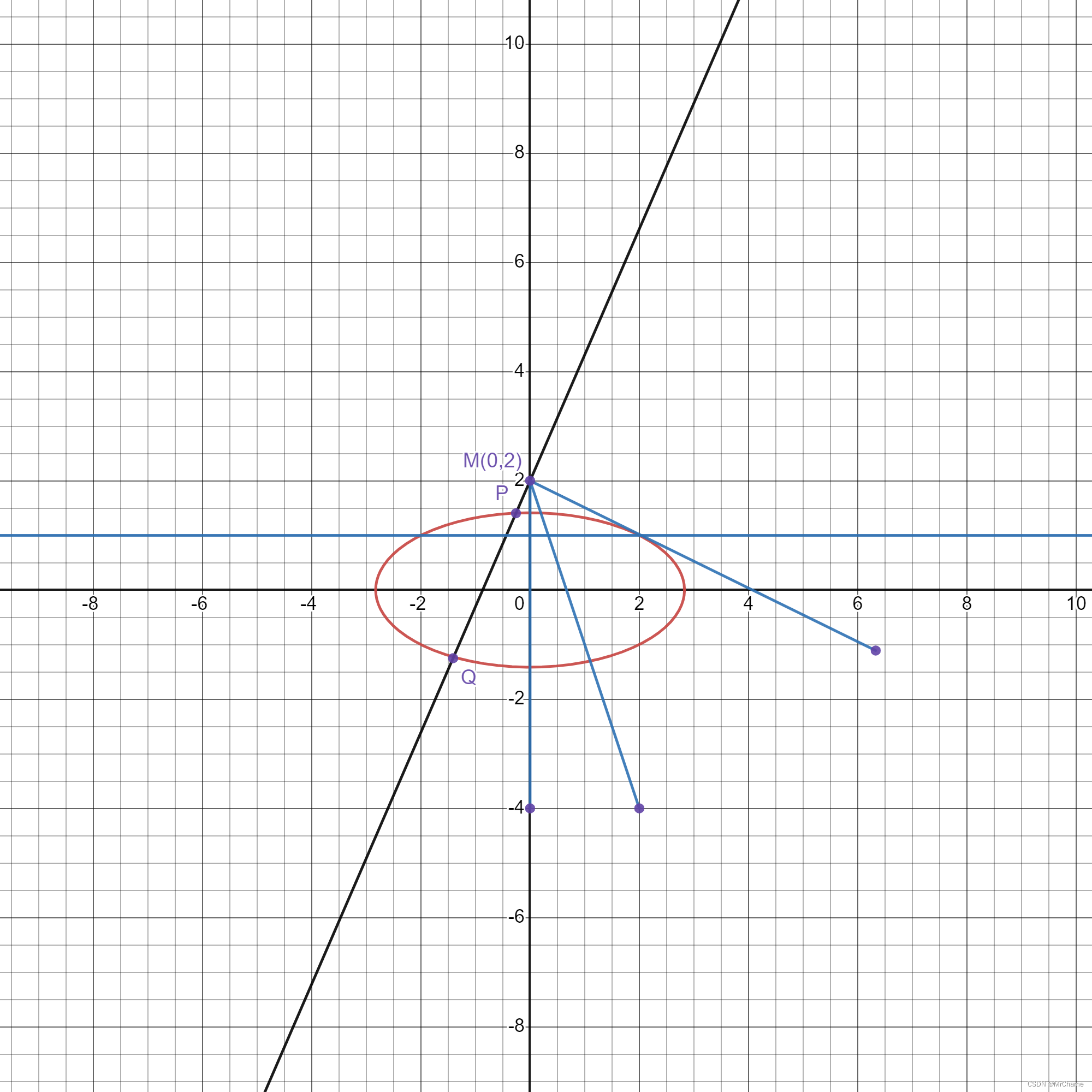
一:调和分割 如图:
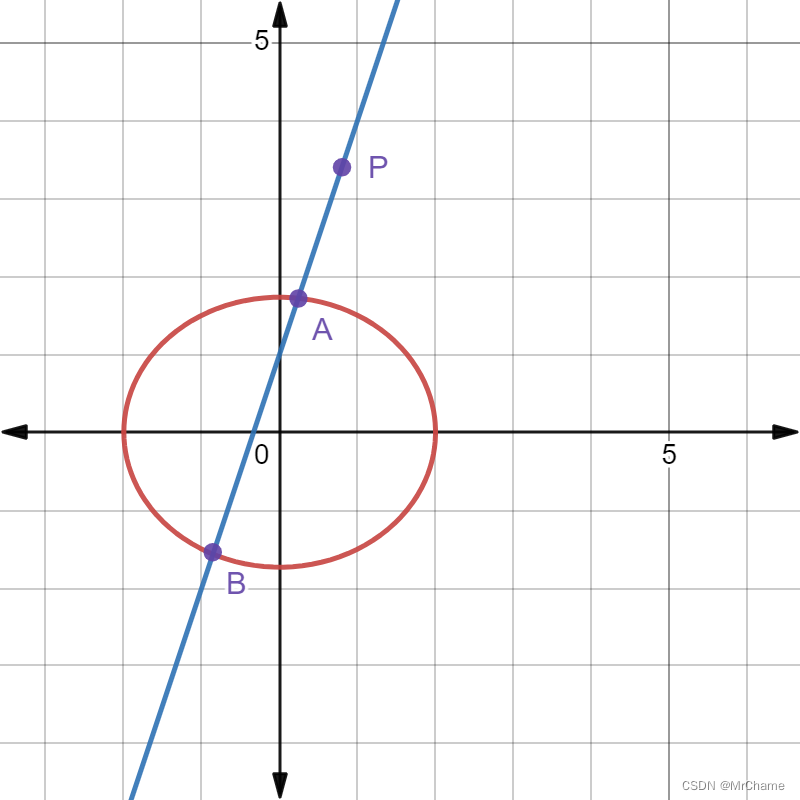
二:定比点差法 如图,直线l交椭圆于AB两点,P为直线上椭圆外一点,若
则有: 由A、B在椭圆上,有: 二式相减并带入 过点P的直线
注1: 极点极线一一对应地成对存在。确定的点P必然对应唯一的极线L,确定的极线L必然对应唯一的极点P。 极点是平面内的任意一点,可在二次曲线外,也可在二次曲线上。 2.极点极线的代数推导:极点极线的一一对应性质,告诉我们知道了平面内一点的坐标,必然可以求出此点关于二次曲线的极线方程,反之亦然。那么,这一一对应的性质是怎么来的?具体该怎么求极点极线?带着这两个问题,我们来研究极点极线的数学推导。 由预备知识,我们只需对 过程中注意负号,具体过程如下:
由A、B在椭圆上,有: 二式相减并带入
联立②③得 由此我们得到:如果我们已知P坐标 以上是以椭圆为例的推导,接下来给出一般二次曲线的极点极线公式推导: 已知二次曲线Ω:
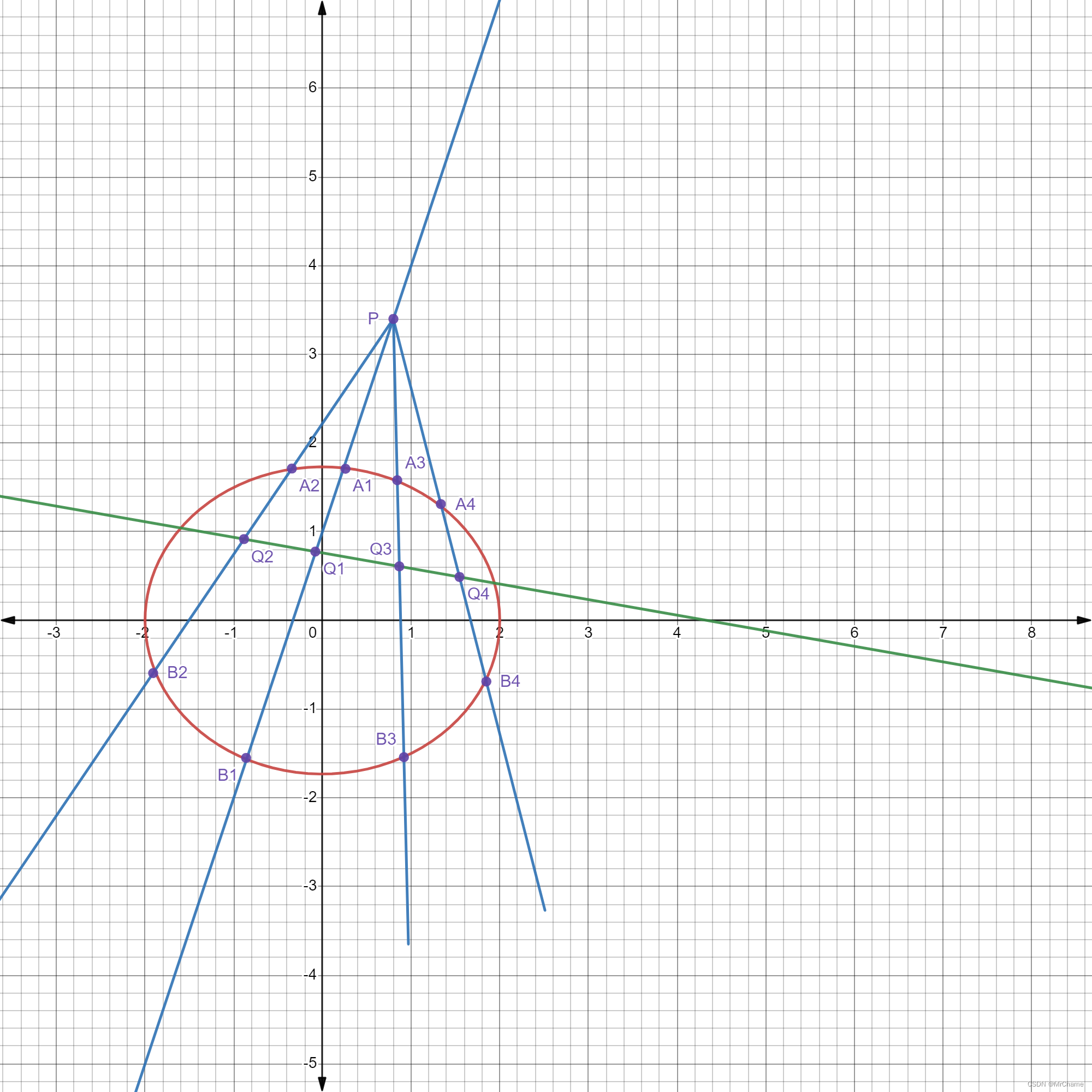
联立①②③④得式 综上所述,对于已知点P 注2: 若极点在二次曲线上,则其对应极线为过该极点的二次曲线的切线。 3.极点极线的性质:极点极线具有很多良好的性质,事实上很多看起来“巧合”的定点定直线题目,背后都蕴含着极点极线的规律。 需要注意的是,由于极点极线规律往往不能直接使用,极点极线的思想对于高考生来说其实是“蒙”答案、开辟思路的方法,而非生搬硬套的“公式”。也正因此,关于极点极线的性质,高考生实则无须学会它们的推导和记忆,有个大概印象,在见到看似是极点极线思想的题目的时候能“蒙”出思路或是答案即可。 极点极线的性质1: 有二次曲线Ω,任意一点P,在点P关于Ω所对应的极线 该性质可由极点极线的代数推导轻易导出。 极点极线的性质2: 有二次曲线Ω,任意直线
简单推导如下: 由注2和性质1,在A所对应的极线PA上取一点P,则P所对应的极线必过A,同理P所对应的极线必过B,故AB即为P所对应的极线,在P所对应的极线上任取一点Q,则Q所对应极线必经过P。 如上,由于笔者不打算引入调和点束等知识,且极点极线其它的性质解释过于复杂,故仅抛出两例。
4.极点极线思想的几道例题:
例①: 已知椭圆
分析: 将题干原式变化得
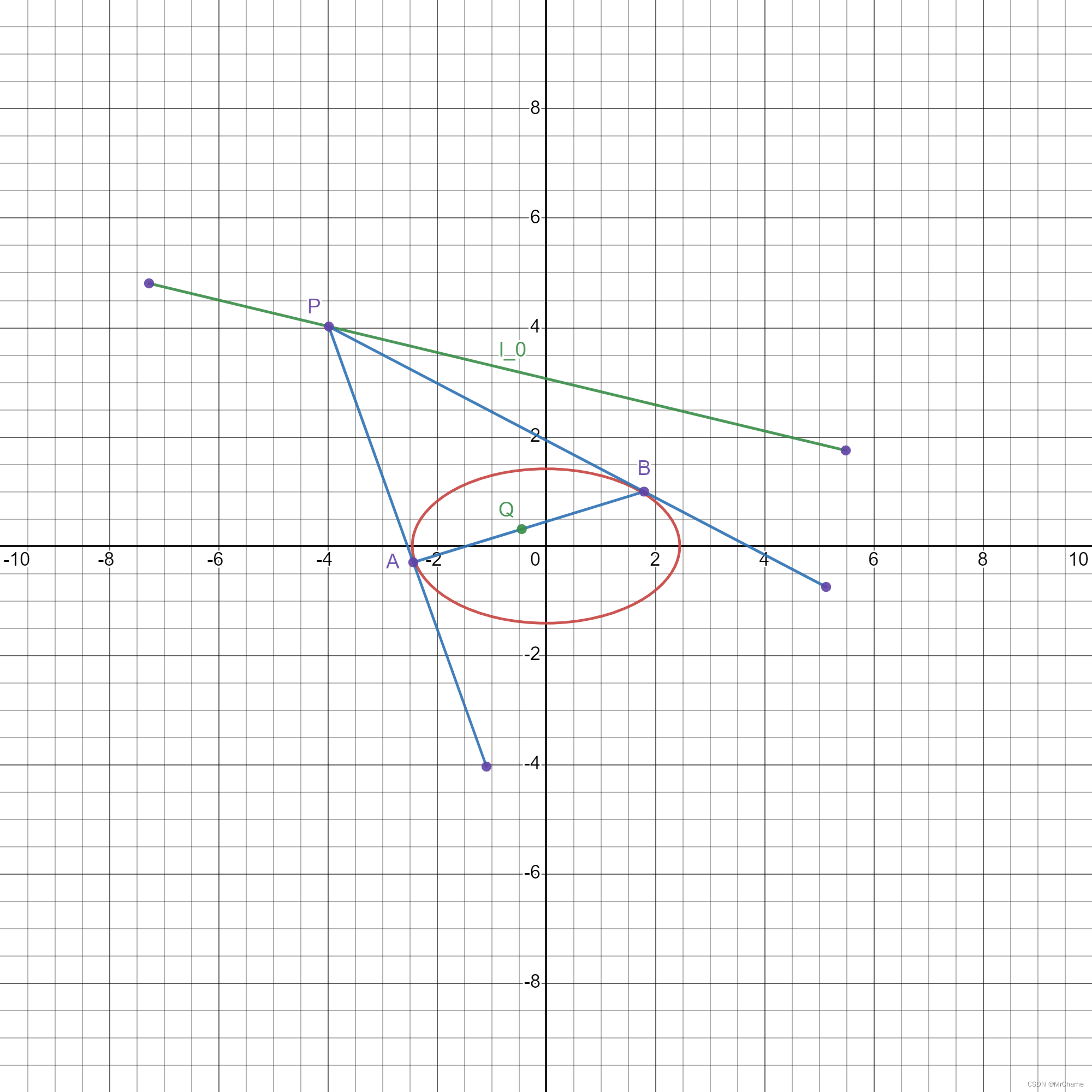
例②
已知椭圆: 分析: 由性质2我们知道AB过定点R,有L方程知R的坐标为(2,3),由OD
极点极线的思想能够帮助解决解析几何中一些常见模型,学会极点极线思想不是背诵好结论,而是形成一种直觉,当题目给定了定点时,迅速考虑其极线在题中是否有用,给定定直线则亦然。 本文例题皆以椭圆为例,其它二次曲线的例题请读者自行研究。 本文尚未给出的较为复杂的极点极线的性质和各色例题,可移步至此进一步研究: 极点极线10个性质以及在近几年全国卷中的应用 (qq.com)
|
【本文地址】
今日新闻 |
推荐新闻 |