平面曲线曲率的计算 |
您所在的位置:网站首页 › 曲率和曲率半径怎么算出来的图片 › 平面曲线曲率的计算 |
平面曲线曲率的计算
|
定义
曲率:曲线上某个点的切线方向角对弧长的变化率,表明曲线在该点的弯曲程度。设有光滑曲线
C
C
C(即曲线
C
C
C 二阶可导),在曲线
C
C
C 上选定一点
M
M
M 作为度量的基点,点
M
M
M 对应于弧长
s
s
s 且切线方向角为
α
\alpha
α,曲线
C
C
C 上另一点
M
′
M'
M′ 对应于弧
s
+
Δ
s
s+\Delta s
s+Δs 且切线方向角为
α
+
Δ
α
\alpha+\Delta \alpha
α+Δα。那么,弧
M
M
′
⌢
\overset{\frown}{MM'}
MM′⌢ 的长度为
∣
Δ
s
∣
|\Delta s|
∣Δs∣,从点
M
M
M 到
M
′
M'
M′ 切线转过的角度为
∣
Δ
α
∣
|\Delta\alpha|
∣Δα∣。平均曲率:采用单位弧长上切线转过的角度来表达弧
M
M
′
⌢
\overset{\frown}{MM'}
MM′⌢ 的平均弯曲程度,称为弧
M
M
′
⌢
\overset{\frown}{MM'}
MM′⌢ 的平均曲率,即:
K
‾
=
∣
Δ
α
∣
∣
Δ
s
∣
\overline{K} = \frac{|\Delta\alpha|}{|\Delta s|}
K=∣Δs∣∣Δα∣曲率:当
Δ
s
→
0
\Delta s\to 0
Δs→0 时,即
M
′
→
M
M'\to M
M′→M 时,平均曲率存在极限,称为曲线
C
C
C 在点
M
M
M 处的曲率,即:
K
=
lim
Δ
s
→
0
∣
Δ
α
∣
∣
Δ
s
∣
=
∣
lim
Δ
s
→
0
Δ
α
Δ
s
∣
K = \lim_{\Delta s\to 0}\frac{|\Delta\alpha|}{|\Delta s|} = |\lim_{\Delta s\to 0}\frac{\Delta\alpha}{\Delta s}|
K=Δs→0lim∣Δs∣∣Δα∣=∣Δs→0limΔsΔα∣
定义公式
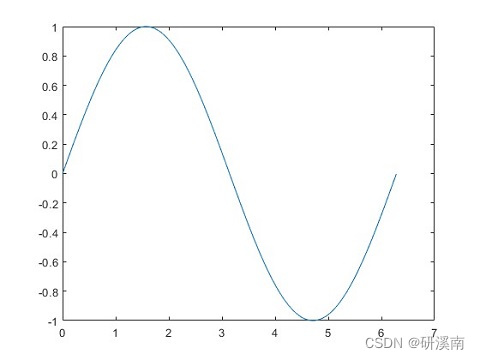
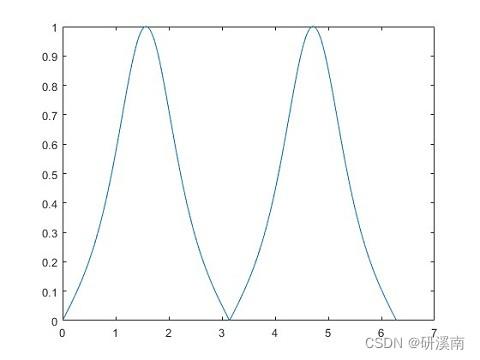
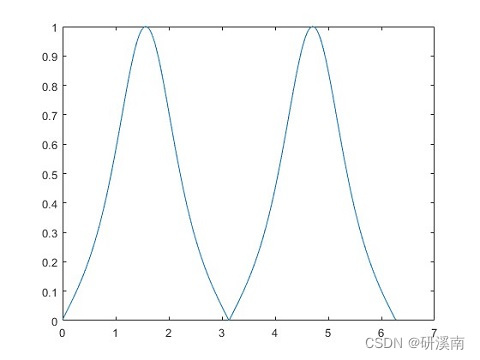
设光滑曲线 C C C 表示为 y = f ( x ) y = f(x) y=f(x),则根据上述定义,有曲率计算公式: K = y ¨ ( 1 + y ˙ 2 ) 3 2 K = \frac{\ddot{y}}{(1+\dot{y}^2)^\frac{3}{2}} K=(1+y˙2)23y¨ 推导过程请参考相关教材或文献。 差分公式然而,对于参数函数 y = y ( t ) , x = x ( t ) y=y(t),x=x(t) y=y(t),x=x(t) 或者离散数据,无法直接采用上述定义公式,上述定义公式经推导得到差分计算公式: K = ∣ x ˙ y ¨ − x ¨ y ˙ ∣ [ x ˙ 2 + y ˙ 2 ] 3 2 K = \frac{|\dot{x}\ddot{y}-\ddot{x}\dot{y}|}{[\dot{x}^2+\dot{y}^2]^\frac{3}{2}} K=[x˙2+y˙2]23∣x˙y¨−x¨y˙∣ MATLAB程序 %% 正弦函数 x = 0:0.01:2*pi; y = sin(x); figure(1); plot(x,y); %% 定义公式 j = abs(sin(x)) ./ ((1+cos(x).^2).^(3/2)); figure(2); plot(x,j); %% 差分公式 x1 = diff(x); % 一阶导 x2 = diff(x1); % 二阶导 y1 = diff(y); y2 = diff(y1); x2(length(x1)) = x2(end); % 使数组维度一致 y2(length(y1)) = y2(end); k = abs(x1.*y2-x2.*y1) ./ (x1.^2+y1.^2).^(3/2); k(length(x)) = k(end); figure(3); plot(x,k);运行结果如下:
|
【本文地址】
今日新闻 |
推荐新闻 |