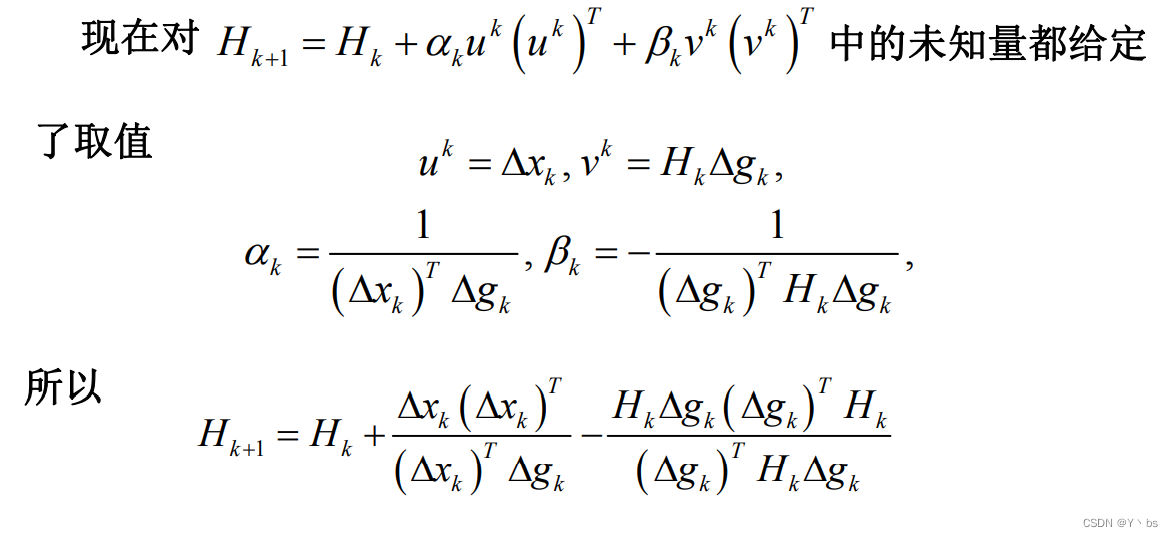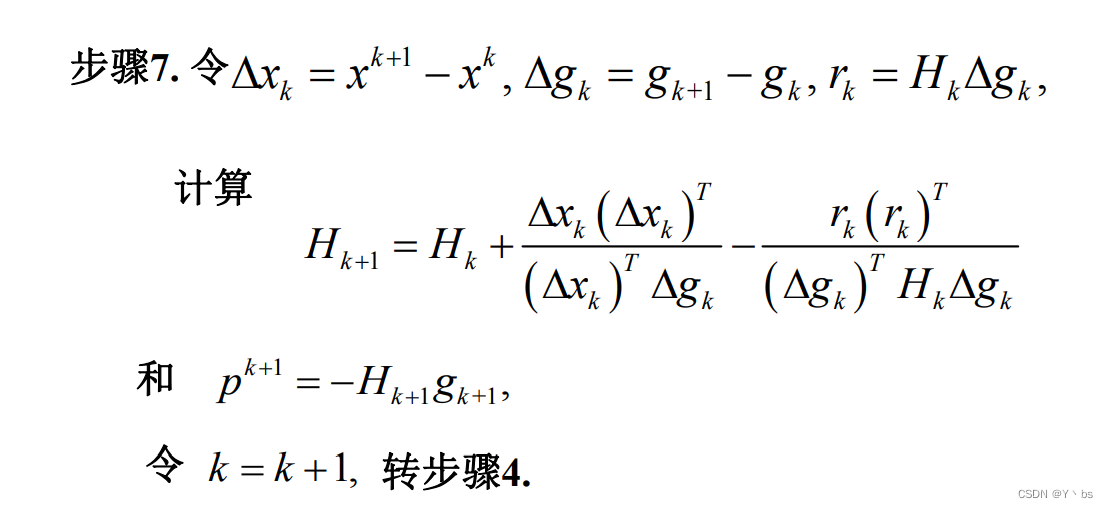无约束最优化方法 |
您所在的位置：网站首页 › 无约束优化例题 › 无约束最优化方法 |
无约束最优化方法
|
文章目录
最速下降法Newton法共轭梯度法变尺度法
无约束最优化问题 m i n f ( x ) f : R n − > R ( 1 ) 求 解 ( 1 ) ， 就 是 找 到 R n 中 的 一 点 x ∗ ， 使 得 ∀ x ∈ R n ， 均 有 f ( x ∗ ) ≤ f ( x ) ， 称 x ∗ 为 ( 1 ) 的 全 局 极 小 点 。 minf(x) \qquad f:R^n->R \qquad (1) \quad \quad \\\quad \quad \newline 求解(1)，就是找到R^n中的一点x^*，使得∀x∈R^n，\quad \quad \\\quad \quad \newline 均有f(x^*)≤f(x)，称x^*为(1)的全局极小点。 \newline minf(x)f:Rn−>R(1)求解(1)，就是找到Rn中的一点x∗，使得∀x∈Rn，均有f(x∗)≤f(x)，称x∗为(1)的全局极小点。 最速下降法
最速下降法的两个特征 相邻两次迭代的搜索方向互相正交 （锯齿现象）对二元正定二次函数，用最速下降法产生的点列：偶数点列均在一条直线上，奇数点列也均在一条直线上，且都过最优点最速下降法的改进： 选择不同初始点采用不精确的一维搜索：采用非精确一维搜索求步长, 可使相邻两个迭代点处的梯度不正交，从而改变收敛性采用加速梯度法：由于最速下降法在极小值点附近成锯齿状，因此下降过程中搜索方向可取 d k = x k − x k − 2 d^k = x^k-x^{k-2} dk=xk−xk−2 下两步继续用最速下降法，即负梯度方向 Newton法
Newton法的优点 当初始点离极小点很近时，算法收敛速度快算法简单，不需要进行一维搜索对正定二次函数，迭代一次就可得到极小点Newton法的缺点 对多数问题算法不具有全局收敛性每次迭代都要计算Hesse矩阵，计算量大 每 次 迭 代 都 要 计 算 ( ▽ 2 f ( x k ) ) − 1 或 求 解 方 程 组 ▽ 2 f ( x k ) d + ▽ f ( x k ) = 0 每次迭代都要计算(▽^2f(x^k))^{-1} \\ \quad \newline 或求解方程组▽^2f(x^k)d+▽f(x^k)=0 每次迭代都要计算(▽2f(xk))−1或求解方程组▽2f(xk)d+▽f(xk)=0( ▽ 2 f ( x k ) ) − 1 可 能 不 存 在 方 程 组 是 奇 异 的 ， 病 态 的 ▽ 2 f ( x k ) 非 正 定 ， d k 可 能 不 是 下 降 方 向 (▽^2f(x^k))^{-1}可能不存在 \\ \quad \newline方程组是奇异的，病态的 \\ \quad \newline ▽^2f(x^k)非正定，d^k可能不是下降方向 (▽2f(xk))−1可能不存在方程组是奇异的，病态的▽2f(xk)非正定，dk可能不是下降方向 收敛于鞍点或极大点的可能性并不小Newton法的改进 针对缺点(1) 对多数算法不具有全局收敛性，和 (4) 收敛于鞍点或极大点的可能性并不小，步长不取固定值1，而是采用精确一维搜索找最佳步长λk,这就是阻尼牛顿法 m i n f ( x k + λ d k ) minf(x^k+λd^k) minf(xk+λdk) Newton法的近一步改进 针对缺点(2)每次计算Hesse矩阵
共轭方向的性质
共轭方向法步骤
FR共轭梯度法 a k = ∣ ∣ g k + 1 ∣ ∣ 2 ∣ ∣ g k ∣ ∣ 2 a_k=\frac{||g_{k+1}||^2}{||g_k||^2} ak=∣∣gk∣∣2∣∣gk+1∣∣2 FR共轭梯度法的计算步骤
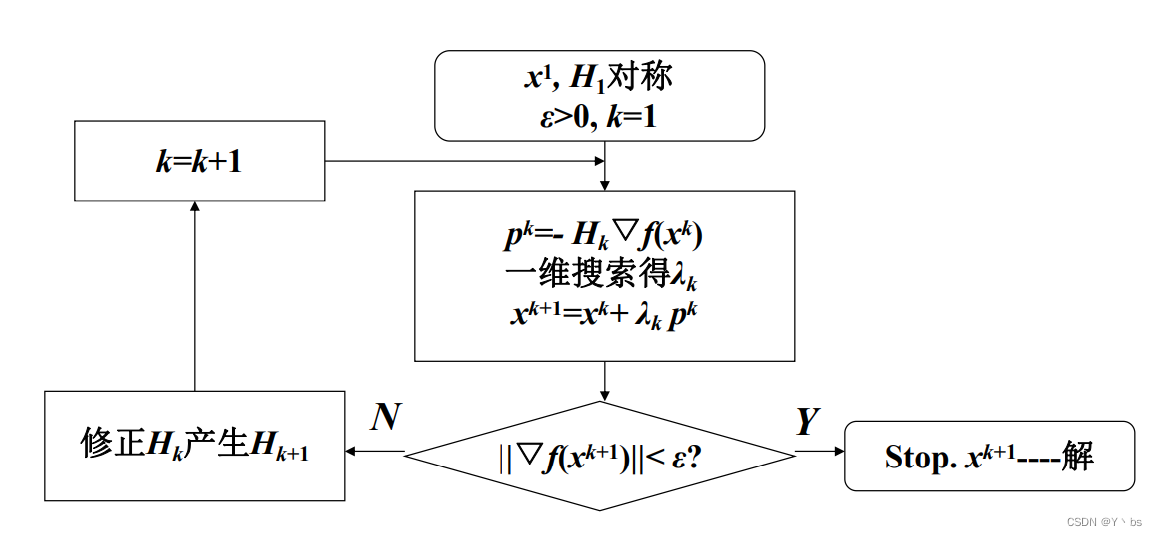
牛顿法和阻尼牛顿法收敛速度很快，但需要计算Hesse矩阵的逆，计算量大 为减少计算量，用一个n阶对称正定矩阵Hk近似代替Hesse矩阵的逆，搜索方向为pk = -Hkgk，由此产生的方法称为变尺度法，Hk为尺度矩阵，这是一种拟牛顿法 变尺度法的计算步骤
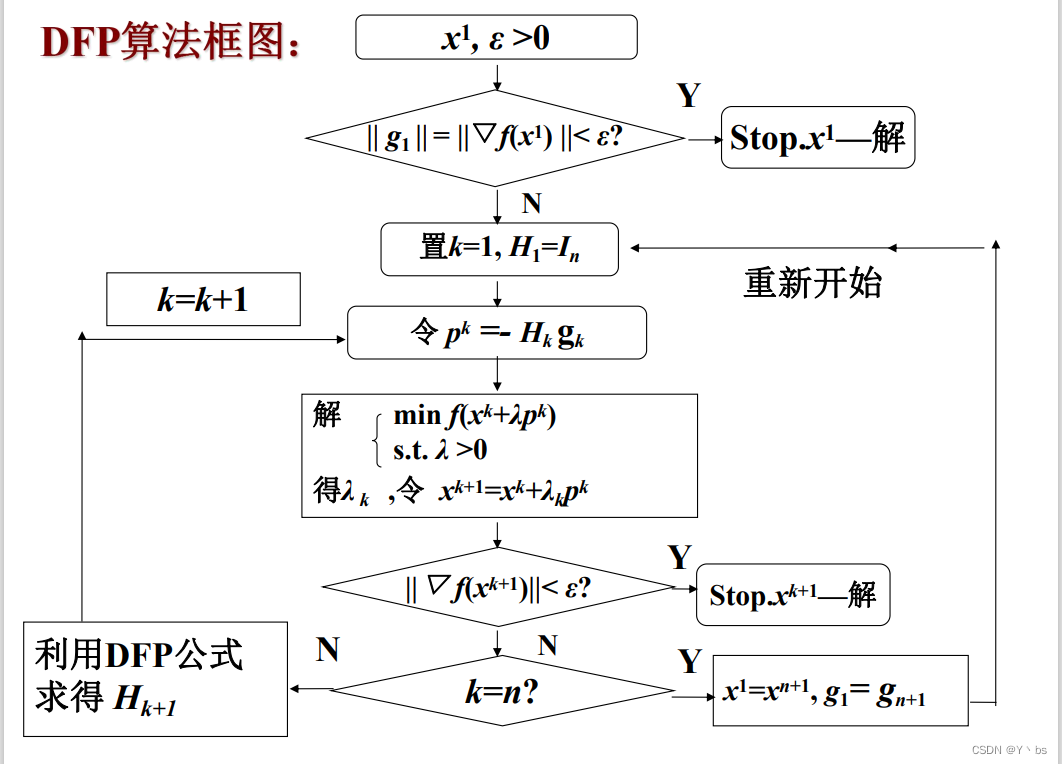
Hk的构造策略 H1为任意一个n阶对称正定矩阵，通常选取n阶单位矩阵I然后通过修正Hk，给出Hk+1 H k + 1 = H k + △ H k H_{k+1} = H_k+△H_k Hk+1=Hk+△Hk 构造不同的Hk，也就是构造不同的修正矩阵△Hk，得到不同的变尺度法DFP算法 DFP算法构造的Hk：对称正定满足拟牛顿性质 H k + 1 △ g k = △ x k H k + 1 = H k + α k u k ( u k ) T + β k v k ( v k ) T α k 、 β k 是 常 数 ， u k 、 v k 是 n 维 列 向 量 ， H 1 是 对 称 正 定 的 矩 阵 H k + 1 满 足 拟 牛 顿 性 质 ， H k + 1 △ g k = △ x k α k u k ( u k ) T △ g k + β k v k ( v k ) T △ g k = △ x k − H k △ g k u k = △ x k ， v k = H k △ g k 令 α k = 1 ( △ x k ) T △ g k ， β k = − 1 ( △ g k ) T H k △ g k H_{k+1}△g_k = △x_k \\ \\ \quad \quad \newline H_{k+1} = H_k +α_ku^k(u^k)^T+β_kv^k(v^k)^T \\ \\\quad \quad \newline α_k、β_k是常数，u^k、v^k是n维列向量，H_1是对称正定的矩阵 \\ \\\quad \quad \newline H_{k+1}满足拟牛顿性质，H_{k+1}△g_k=△x_k \\ \\\quad \quad \newline α_ku^k(u^k)^T△g_k +β_kv^k(v^k)^T△g_k=△x_k-H_k△g_k\\ \\\quad \quad \newline u^k=△x_k，v^k=H_k△g_k\\ \\\quad \quad \newline 令α_k = \frac{1}{(△x_k)^T△g_k}，β_k=-\frac{1}{(△g_k)^TH_k△g_k} Hk+1△gk=△xkHk+1=Hk+αkuk(uk)T+βkvk(vk)Tαk、βk是常数，uk、vk是n维列向量，H1是对称正定的矩阵Hk+1满足拟牛顿性质，Hk+1△gk=△xkαkuk(uk)T△gk+βkvk(vk)T△gk=△xk−Hk△gkuk=△xk，vk=Hk△gk令αk=(△xk)T△gk1，βk=−(△gk)THk△gk1
DFP算法的计算步骤
|
步骤3中的搜房方向，可通过求解下列方程组得到
▽
2
f
(
x
k
)
d
k
+
▽
f
(
x
k
)
=
0
▽^2f(x^k)d^k+▽f(x^k)=0
▽2f(xk)dk+▽f(xk)=0
【本文地址】
今日新闻 |
推荐新闻 |