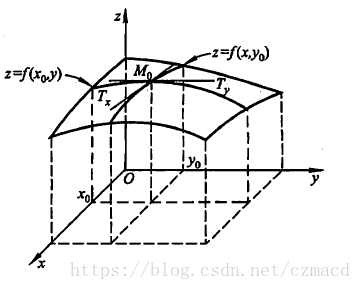
学习到机器学习线性回归和逻辑回归时遇到了梯度下降算法，然后顺着扯出了一堆高数的相关概念理论：导数、偏导数、全微分、方向导数、梯度，重新回顾它们之间的一些关系，从网上和教材中摘录相关知识点。

定义：设函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0​的某个领域内有定义，如果 Δ y Δ x \frac{Δy}{Δx} ΔxΔy​在当 Δ x Δx Δx->0时极限存在，则称函数 y = f ( x ) y=f(x) y=f(x)在 x 0 x_0 x0​处可导，这个极限是函数 y = f ( x ) y=f(x) y=f(x)在 x 0 x_0 x0​处的导数 f ′ ( x 0 ) = lim ⁡ Δ x → 0 Δ y Δ x = lim ⁡ Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim \limits_{Δx \to 0} \frac{Δy}{Δx}=\lim \limits_{Δx \to 0} \frac{f(x_0+Δx)-f(x_0)}{Δx} f′(x0​)=Δx→0lim​ΔxΔy​=Δx→0lim​Δxf(x0​+Δx)−f(x0​)​

根据导数的定义，从某种意义上说导数的本质是一种极限

导数与导函数的关系是局部与整体的关系，导数通常是指一点，导函数则是指一个区间上的

定义：设函数 y = f ( x ) y=f(x) y=f(x)在某个领域内有定义， x 0 x_0 x0​及 x 0 + Δ x x_0+Δx x0​+Δx在这区间内，如果增量 Δ y = f ( x 0 + x ) − f ( x 0 ) Δy=f(x_0+x)-f(x_0) Δy=f(x0​+x)−f(x0​) 可表示为 Δ y = A Δ x + o ( Δ x ) Δy=AΔx+o(Δx) Δy=AΔx+o(Δx) 其中A是不依赖 Δ x Δx Δx的常数， o ( Δ x ) o(Δx) o(Δx)是指 Δ x Δx Δx趋于0时的高阶无穷小，那么称函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0​是可微的，而 A Δ x AΔx AΔx叫做函数在点 x 0 x_0 x0​相应于自变量增量 Δ x Δx Δx的微分，记作 d y \mathrm{d} y dy，记作 d y = A Δ x \mathrm{d}y=AΔx dy=AΔx

高阶无穷小的定义：如果 lim ⁡ β α = 0 \lim \limits \frac{\beta}{\alpha}=0 limαβ​=0，就说 β \beta β是比 α \alpha α高阶的无穷小，记作 β = o ( α ) \beta=o(\alpha) β=o(α)

上式 Δ y = A Δ x + o ( Δ x ) Δy=AΔx+o(Δx) Δy=AΔx+o(Δx)两边同时除以 Δ x Δx Δx得到 Δ y Δ x = A + o ( Δ x ) Δ x \frac{Δy}{Δx}=A+\frac{o(Δx)}{Δx} ΔxΔy​=A+Δxo(Δx)​ 当 Δ x → 0 Δx \to 0 Δx→0时,上式左边就是导数的定义，而右边的 o ( Δ x ) Δ x \frac{o(Δx)}{Δx} Δxo(Δx)​因为是高阶无穷小，所以会趋向于0，得到以下等式 A = lim ⁡ Δ x → 0 Δ y Δ x = f ′ ( x 0 ) A=\lim \limits_{Δx \to 0}\frac{Δy}{Δx}=f'(x_0) A=Δx→0lim​ΔxΔy​=f′(x0​) 因此，如果函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0​可微，则 f ( x ) f(x) f(x)在点 x 0 x_0 x0​也一定可导，且 A = f ′ ( x 0 ) A=f'(x_0) A=f′(x0​)，反之，如果 f ( x ) f(x) f(x)在点 x 0 x_0 x0​可导，存在下式 lim ⁡ Δ x → 0 Δ y Δ x = f ′ ( x 0 ) \lim \limits_{Δx \to 0}\frac{Δy}{Δx}=f'(x_0) Δx→0lim​ΔxΔy​=f′(x0​) 根据极限与无穷小的关系转化上式，当 Δ x → 0 Δx \to 0 Δx→0时 Δ y Δ x = f ′ ( x 0 ) + α \frac{Δy}{Δx}=f'(x_0)+\alpha ΔxΔy​=f′(x0​)+α 其中 lim ⁡ Δ x → 0 a = 0 \lim \limits_{Δx \to 0}a=0 Δx→0lim​a=0，即 lim ⁡ Δ x → 0 a Δ x Δ x = 0 \lim \limits_{Δx \to 0}\frac{aΔx}{Δx}=0 Δx→0lim​ΔxaΔx​=0, a Δ x = o ( Δ x ) aΔx=o(Δx) aΔx=o(Δx)，上式转化为下式(又回到了微分的定义) Δ y = f ′ ( x 0 ) Δ x + o ( Δ x ) Δy=f'(x_0)Δx+o(Δx) Δy=f′(x0​)Δx+o(Δx) 因此，函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0​可微的充分必要条件是函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0​可导 d y = f ′ ( x 0 ) Δ x \mathrm{d}y=f'(x_0)Δx dy=f′(x0​)Δx

一元函数的变化率是导数，多元函数的自变量有多个，当某个自变量x变化而其它自变量固定时，这时候对变化的自变量x进行求导，就称为多元函数对于x的偏导数。 定义：设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)的某一领域内有定义，当 y y y固定于 y 0 y_0 y0​，而 x x x在 x 0 x_0 x0​处有增量 Δ x Δx Δx，相应的函数有增量 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) f(x_0+Δx,y_0)-f(x_0,y_0) f(x0​+Δx,y0​)−f(x0​,y0​) 如果 lim ⁡ Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \lim \limits_{Δx \to 0}\frac{f(x_0+Δx,y_0)-f(x_0,y_0)}{Δx} Δx→0lim​Δxf(x0​+Δx,y0​)−f(x0​,y0​)​ 存在，则称该极限为 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处对 x x x的偏导数

偏导数的几何意义

很多时候要考虑多元函数沿任意方向的变化率，那么就引出了方向导数

参考上文微分的定义，与一元函数的情形一样，希望用自变量增量 Δ x , Δ y Δx,Δy Δx,Δy来线性函数来代替函数的全增量 Δ z Δz Δz，从而减化计算 定义：设函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)的某领域内有定义如果函数在点 ( x , y ) (x,y) (x,y)的全增量 Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) Δz=f(x+Δx,y+Δy)-f(x,y) Δz=f(x+Δx,y+Δy)−f(x,y) 可心表示为 Δ z = A Δ x + B Δ y + o ( ρ ) Δz=AΔx+BΔy+o(\rho) Δz=AΔx+BΔy+o(ρ) 其中 A , B A,B A,B不依赖于 Δ x , Δ y Δx,Δy Δx,Δy， ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(Δx)^2+(Δy)^2} ρ=(Δx)2+(Δy)2 ​，则称函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x , y ) (x,y) (x,y)处可微分，而 A Δ x + B Δ y AΔx+BΔy AΔx+BΔy称为函数在点 ( x , y ) (x,y) (x,y)的全微分 d z = A Δ x + B Δ y \mathrm{d}z=AΔx+BΔy dz=AΔx+BΔy

基于上述全微分定义成立，存在某一点 p ′ ( x + Δ x , y + Δ y ) p'(x+Δx,y+Δy) p′(x+Δx,y+Δy)对于式子 Δ z = A Δ x + B Δ y + o ( ρ ) Δz=AΔx+BΔy+o(\rho) Δz=AΔx+BΔy+o(ρ)也成立，当 Δ y = 0 Δy=0 Δy=0时 f ( Δ x + x , y ) − f ( x , y ) = A Δ X + o ( ∣ Δ x ∣ ) f(Δx+x,y)-f(x,y)=AΔX+o(|Δx|) f(Δx+x,y)−f(x,y)=AΔX+o(∣Δx∣) 两边除以 Δ x Δx Δx并且令 Δ x → 0 Δx \to 0 Δx→0取极限 lim ⁡ Δ x → 0 f ( x + Δ x , y ) − f ( x , y ) Δ x = A \lim \limits_{Δx \to 0}\frac{f(x+Δx,y)-f(x,y)}{Δx}=A Δx→0lim​Δxf(x+Δx,y)−f(x,y)​=A 这式子就是偏导数的定义形式啊，所以这说明了偏导数 f x ( x , y ) f_x(x,y) fx​(x,y)存在且等于 A A A，同理也可证 f y ( x , y ) = B f_y(x,y)=B fy​(x,y)=B，由此推导出以下公式 d z = f x ( x , y ) Δ x + f y ( x , y ) Δ y \mathrm{d}z=f_x(x,y)Δx+f_y(x,y)Δy dz=fx​(x,y)Δx+fy​(x,y)Δy

各偏导数的存在只是全微分存在的必要条件而非充分条件，即由全微分可证各偏导数存在，反之则不行

如果函数的各个偏数在点 ( x , y ) (x,y) (x,y)是连续的，则函数可微分

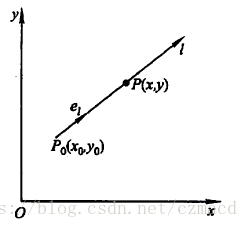
定义导数、偏导数、方向导数都是说如果说某条件下极限存在，谨记导数的本质是极限及代表函数的变化率，偏导数反映的是函数沿坐标轴方向的变化率，有所限制，所以引入方向导数表示沿任意一方向的变化率 定义：设 l l l是 x O y xOy xOy平面以 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0​(x0​,y0​)为始点的一条射线， e i = ( c o s α , c o s β ) e_i=(cos\alpha,cos\beta) ei​=(cosα,cosβ)是以射线同方向的单位向量

射线 l l l的参数方程为 { x = x 0 + t c o s α ， t ≥ 0 y = y 0 + t c o s β ， t ≥ 0 \begin{cases}x=x_0+tcos\alpha ，t\geq0\\ y=y_0+tcos\beta，t\geq0 \end{cases} {x=x0​+tcosα，t≥0y=y0​+tcosβ，t≥0​ 如果函数增量 f ( x 0 + t c o s α , y 0 + t c o s β ) − f ( x 0 , y 0 ) f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0) f(x0​+tcosα,y0​+tcosβ)−f(x0​,y0​)与 P P P到 P 0 P_0 P0​的距离 ∣ P P 0 ∣ = t |PP_0|=t ∣PP0​∣=t的比值，当点 P P P沿着 l l l趋于 P 0 ( 即 t → 0 + ) P_0(即t \to 0^+) P0​(即t→0+)时极限存在，则称此极限为函数在点 P 0 P_0 P0​沿方向 l l l的方向导数 ∂ f ∂ l ∣ ( x 0 , y 0 ) = lim ⁡ t → 0 + f ( x 0 + t c o s α , y 0 + t c o s β ) − f ( x 0 , y 0 ) t \frac{\partial f}{\partial l}|_{(x_0,y_0)}=\lim \limits_{t \to 0^+}\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0)}{t} ∂l∂f​∣(x0​,y0​)​=t→0+lim​tf(x0​+tcosα,y0​+tcosβ)−f(x0​,y0​)​

由全微分的定义得到 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y + o ( ( Δ x ) 2 + ( Δ y ) 2 ) f(x_0+Δx,y_0+Δy)-f(x_0,y_0)=f_x(x_0,y_0)Δx+f_y(x_0,y_0)Δy+o(\sqrt{(Δx)^2+(Δy)^2}) f(x0​+Δx,y0​+Δy)−f(x0​,y0​)=fx​(x0​,y0​)Δx+fy​(x0​,y0​)Δy+o((Δx)2+(Δy)2 ​) 设点 ( x 0 + Δ x , y 0 + Δ y ) (x_0+Δx,y_0+Δy) (x0​+Δx,y0​+Δy)在以 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)为起点的射线 l ( c o s α , c o s β 是 l 的方向余弦 ) l(cos\alpha,cos\beta是l的方向余弦) l(cosα,cosβ是l的方向余弦)上，则有 Δ x = t c o s α Δx=tcos\alpha Δx=tcosα, Δ y = t c o s β Δy=tcos\beta Δy=tcosβ, ( Δ x ) 2 + ( Δ y ) 2 = t \sqrt{(Δx)^2+(Δy)^2}=t (Δx)2+(Δy)2 ​=t，所以 lim ⁡ t → 0 + f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) t = f x ( x 0 , y 0 ) c o s α + f y ( x 0 , y 0 ) c o s β \lim \limits_{t \to 0^+}\frac{f(x_0+Δx,y_0+Δy)-f(x_0,y_0)}{t}=f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta t→0+lim​tf(x0​+Δx,y0​+Δy)−f(x0​,y0​)​=fx​(x0​,y0​)cosα+fy​(x0​,y0​)cosβ 上式左侧就是方向导数定义形式，极限存在即方向导数存在，且其值等于右式

由此得到定理，如果函数 f ( x , y ) f(x,y) f(x,y)在点 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0​(x0​,y0​)可微分，那么函数在该点沿任一方向 l l l的方向导数存在 ∂ f ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) c o s α + f y ( x 0 , y 0 ) c o s β \frac{\partial f}{\partial l}|_{(x_0,y_0)}=f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta ∂l∂f​∣(x0​,y0​)​=fx​(x0​,y0​)cosα+fy​(x0​,y0​)cosβ

在平面上确定某一点可能存在无数个方向导数，我们怎样找到其中一个方向导数来描述函数最大变化率？ 定义：在二元函数的情形， 设函数 f ( x , y ) f(x,y) f(x,y)在平面区域D内具有一阶连续偏导数，对于每一点 P 0 ( x 0 , y 0 ) ∈ D P_0(x_0,y_0)\in D P0​(x0​,y0​)∈D，都可以给出一个向量 f x ( x 0 , y 0 ) i + f y ( x 0 , y 0 ) j 或用坐标表示 ( f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) ) f_x(x_0,y_0)i+f_y(x_0,y_0)j \quad 或用坐标表示 \quad (f_x(x_0,y_0),f_y(x_0,y_0)) fx​(x0​,y0​)i+fy​(x0​,y0​)j或用坐标表示(fx​(x0​,y0​),fy​(x0​,y0​)) 其中 i , j i,j i,j为 x , y x,y x,y轴的方向向量，上述微量称为函数 f ( x , y ) f(x,y) f(x,y)在点 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0​(x0​,y0​)的梯度记作 g r a d f ( x 0 , y 0 ) = f x ( x 0 , y 0 ) i + f y ( x 0 , y 0 ) j gradf(x_0,y_0)=f_x(x_0,y_0)i+f_y(x_0,y_0)j gradf(x0​,y0​)=fx​(x0​,y0​)i+fy​(x0​,y0​)j 由定义看到，梯度的方向是确定的，如果点 P P P的坐标确定，那么梯度也大小也确定

如果函数 f ( x , y ) f(x,y) f(x,y)在点 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0​(x0​,y0​)可微分， e l = ( c o s α , c o s β ) e_l=(cos\alpha,cos\beta) el​=(cosα,cosβ)是方向 l l l的方向向量(方向未确定) ∂ f ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) c o s α + f y ( x 0 , y 0 ) c o s β = g r a d   f ( x 0 , y 0 ) . e l = ∣ g r a d   f ( x 0 , y 0 ) ∣ c o s θ \frac{\partial f}{\partial l}|_{(x_0,y_0)}=f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta=grad\ f(x_0,y_0).e_l=|grad\ f(x_0,y_0)|cos\theta ∂l∂f​∣(x0​,y0​)​=fx​(x0​,y0​)cosα+fy​(x0​,y0​)cosβ=grad f(x0​,y0​).el​=∣grad f(x0​,y0​)∣cosθ 其中 θ \theta θ为向量 g r a d   f ( x 0 , y 0 ) {grad\ f(x_0,y_0)} grad f(x0​,y0​)与向量 e l e_l el​的夹角，当 θ = 0 \theta=0 θ=0时，即方向 e l e_l el​与梯度 g r a d   f ( x 0 , y 0 ) {grad\ f(x_0,y_0)} grad f(x0​,y0​)的方向时，函数 f ( x , y ) f(x,y) f(x,y)增加最快，函数在这个方向的方向导数达到最大值，这个值就是梯度 g r a d   f ( x 0 , y 0 ) {grad\ f(x_0,y_0)} grad f(x0​,y0​)的模，即 ∂ f ∂ l ∣ ( x 0 , y 0 ) = ∣ g r a d   f ( x 0 , y 0 ) ∣ \frac{\partial f}{\partial l}|_{(x_0,y_0)}=|grad \ f(x_0,y_0)| ∂l∂f​∣(x0​,y0​)​=∣grad f(x0​,y0​)∣

所以可以用沿梯度方向的方向导数来描述是函数最大变化率，即梯度方向是函数变化率最大的方向，在梯度定义的时候就已经赋予了它这个特性。