【A |
您所在的位置:网站首页 › 指数方程在线求解 › 【A |
【A
|
在《对数运算(Logarithm)》一文中详细介绍了对数的运算规则与性质,如果不清楚的可以先熟悉一下 本文介绍A-Level考试中常考的对数、指数方程及不等式的题型及求解方法。 主要分三块内容: (1)求解对数、指数方程(组)(2)求解对数、指数不等式(3)利用对数进行线性变化求解未知参数的值(1)求解对数、指数方程(组)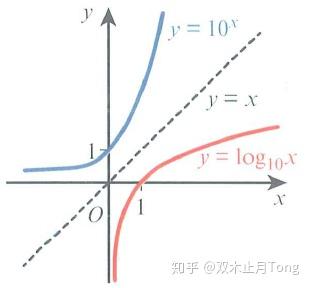 原理:在求解对数与指数方程时一般都化成 \log_a f(x)=\log_a g(x) 或者 a^{f(x)}=a^{g(x)} ,然后就可以推得 f(x)=g(x) 。这里主要是借助了对数函数与指数函数都是一一对应函数(one-to-one function),也就是一个自变量对应一个应变量。如果一个自变量对应两个或者多个应变量就没有这样的结论了,比如二次函数等。 问题一:求解对数方程 Solve:a. 2 \log _{8}(x+2)=\log _{8}(2 x+19) b. 4 \log _{x} 2-\log _{x} 4=2 Answer: a. \begin{aligned} 2 \log _{8}(x+2) &=\log _{8}(2 x+19) \\ \log _{8}(x+2)^{2} &=\log _{8}(2 x+19) \\(x+2)^{2} &=2 x+19 \\ x^{2}+4 x+4 &=2 x+19 \\ x^{2}+2 x-15 &=0 \\(x-3)(x+5) &=0 \end{aligned} x=3 或 x=-5 当 x=3 时, \log_85,\log_825 都有定义;当 x=-5 时, 2 \log _{8}(x+2)=2 \log _{8}(-3) 没有定义,故舍去。综上, \boxed{x=3} .注意:求解对数方程一定要把根代回去验证一下是否有定义! b. \begin{aligned} \log _{x} 2^{4}-\log _{x} 2^{2} &=2 \\ \log _{x} 2^{4-2} &=2 \\ \log _{x} 2^{2} &=2 \\ \log _{x} 4 &=2 \\ x^{2} &=4 \\ x &=\pm 2 \end{aligned} 当 x=-2 时,无意义,舍去;故, \boxed{x=2} 是方程的根.问题二:求解指数方程 Solve:a. 3^{2 x}=4^{x+5} b. 2(3^{2x})+7(3^x)=15 c. 8(8^{x-1}-1)=7(4^x-2^{x+1}) Answer:a. \begin{aligned} 3^{2 x} &=4^{x+5} \\ \log 3^{2 x} &=\log 4^{x+5} \\ 2 x \log 3 &=(x+5) \log 4 \\ 2 x \log 3 &=x \log 4+5 \log 4 \\ x(2 \log 3-\log 4) &=5 \log 4 \\ x &=\frac{5 \log 4}{2 \log 3-\log 4} \end{aligned}注:一般的指数方程都可以借助“取对数”这个技巧来处理,将其转化为线性方程。 b.令 y=3^x \begin{aligned} 2\left(3^{2 x}\right)+7\left(3^{x}\right)-15 &=0 \\ 2 y^{2}+7 y-15 &=0 \\(2 y-3)(y+5) &=0 \\ y=1.5 \text { or } y &=-5 \end{aligned} 因为 y=3^x>0 所以 y=1.5 于是 \begin{aligned} 3^{x} &=1.5 \\ x \log 3 &=\log 1.5 \\ x &=\frac{\log 1.5}{\log 3} \end{aligned} .注:“整体代换”是求解指数方程常见的方程,在高中阶段我们只学过一元一次方程、一元二次方程的求解,遇到高次、指数都可以考虑整体代换。 c.化简可得 8^x-8=7(4^x-2\cdot 2^x) 令 y=2^x 上式变为 t^3-8=7(t^2-2t) t^3-7t^2+14t-8=0 因为 t=1 是上述方程的一个根,所以必定存在 t-1 的因子,可得下式: (t-1)(t^2-6t+8)=0 (t-1)(t-2)(t-4)=0 所以: 2^x=1,2^x=2,2^x=4 \boxed{x=0,1,2} .注:这里还是运用了换元的方法转化成了一元三次方程,这里需要根据因子定理进行因式分解,不清楚可以参看《余数定理》和《高次方程求根》。 问题三:求解对数、指数方程组 Solve:a. \left\{\begin{array}{l}{4^x=2^y} \\ {3\log_{10}y=\log_{10}x+\log_{10}2} \end{array}\right. b. \left\{\begin{array}{l}{e^{3x+4y}=2e^{2x-y}} \\ {e^{2x+y}=8e^{x+6y}} \end{array}\right. Answer:a.根据第一个式子可知: 4^x=(2^2)^x=2^{2x}=2^y\Rightarrow2x=y 根据第二个式子可知: \log_{10}y^3=\log_{10}2x\Rightarrow y^3=2x 结合两式, y^3-y=0\Rightarrow y(y+1)(y-1)=0 又因为 \log_{10}y 有定义, y>0 所以, \left\{\begin{array}{l}{x=0.5} \\ {y=1} \end{array}\right.注:对数与指数方程组求解与我们之前所接触的二元一次的方程组求解是类似的,只不过多了一步通过对数与指数的化简得到 x,y 之间的关系。 b.对第一个式子两边取ln可知: 3x+4y=\ln2+2x-y\Rightarrow x+5y=\ln2 对第二个式子两边取ln可知: 2x+y=\ln8+x+6y\Rightarrow x-5y=\ln8 于是: x=\frac{\ln16}{2}=2\ln2 y=-\frac{\ln2}{5} (2)求解对数、指数不等式Solve:a. 0.6^{x}4 \times 3^{2 x-1}>5 Answer:a. \begin{aligned} 0.6^{x} &\begin{aligned} 4 \times 3^{2 x-1} &>5 \\ 3^{2 x-1} &>\frac{5}{4} \\(2 x-1) \log 3 &>\log \frac{5}{4} \\(2 \log 3) x-\log 3 &>\log \frac{5}{4} \\ x &>\frac{\log \frac{5}{4}+\log 3}{2 \log 3} \\ x &>\frac{\log \frac{15}{4}}{\log 9} \end{aligned}注:求解不等式时要注意两点: (1)取对数时一般取 \log 或 \ln 底大于1,不等式符号不变; (2)再除时要判断一下值是否小于0;   (3)利用对数进行线性变化求解未知参数的值 (3)利用对数进行线性变化求解未知参数的值Question:  Answer: 两边取对数可得: \begin{array}{l}{\ln y=\ln \left(a \times e^{-b x^{2}}\right)} \\ {\ln y=\ln a+\ln e^{-b x}} \\ {\ln y=\ln a-b x^{2}} \\ {\ln y=-b x^{2}+\ln a}\end{array} 那么就得到了 \ln y, x^2 的直线表达, Y=m X+c 。根据图像可知直线过(0.55,0.84),(1.72,0.26)两点,可算得直线斜率和截距 m=\frac{0.26-0.84}{1.72-0.55}=-0.4957\Rightarrow b\approx 0.5 c=1.1126\Rightarrow \ln a=1.1126\Rightarrow a\approx 3.04注:对于型如 y=ae^{bx} 的表达式,我们都可以用取对数的方法把他转化为 Y=m X+c 的线性关系。这种方法在数据处理上还是挺常见的。 本文主要介绍了A-Level中对数、指数常见的考察方式,关键还是熟悉对数、指数的运算规则与性质,掌握其本质原理,那么题目无论怎么变都能游刃有余。 一己拙见,欢迎交流讨论~ 想了解更多国际数学课程,可参看: |
【本文地址】