时域混叠和频域混叠 |
您所在的位置:网站首页 › 抽样定理和频谱混叠关系 › 时域混叠和频域混叠 |
时域混叠和频域混叠
|
时域混叠和频域混叠
含义
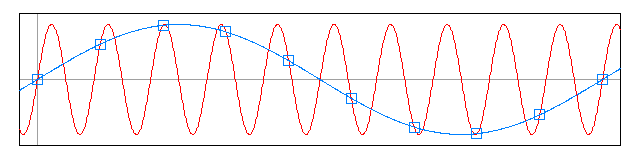
混叠(英语:Aliasing),在信号频谱上可称作叠频;在影像上可称作叠影,主要来自于对连续时间信号作取样以数字化时,取样频率低于两倍奈奎斯特频率。
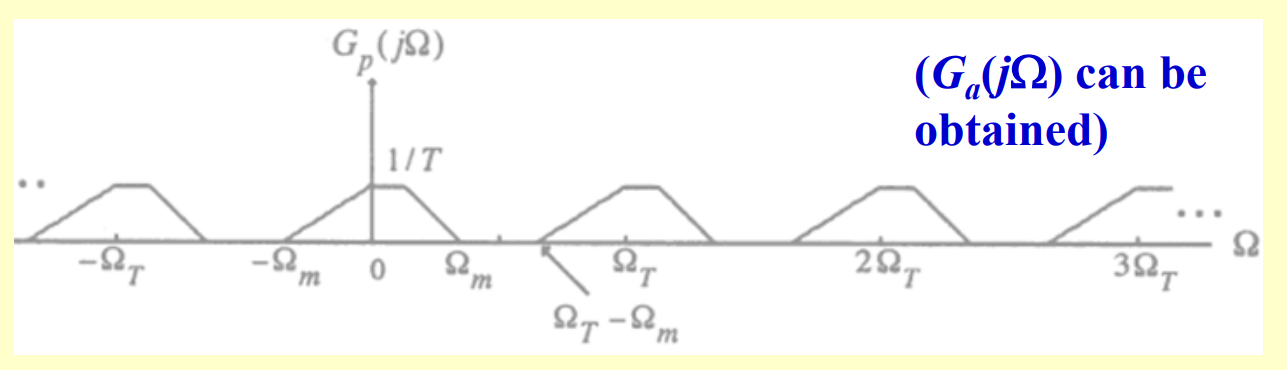
如上图,以相同的采样周期对一个高频信号和低频信号进行采样,采出的数字序列相同,此时发生混叠。 解释一下奈奎斯特频率一个信号的奈奎斯特频率由该信号中的最高频率分量决定,例如某个信号的傅里叶展开表达式如下: \[f(t)=cos\pi t +cos 2\pi t + cos4\pi t \tag{1} \]那么,该信号的奈奎斯特频率为2Hz,因此,根据上述混叠的定义,为了避免混叠,采样频率必须大于4Hz,采样周期必须小于\(\frac{1}{4}\) s 。该特性又叫采样定理。 研究一下为什么会产生混叠 频域是什么首先,这里提一嘴,所谓频域只是学者为了研究方便所提出的一个数学概念,因此,它必然拥有一种特性,那就是,它可以方便计算但是难以形象的理解,因为我们的生活是在时域里的,我们的常识也是基于时间的,这让我们更能理解周期而不是频率。但是,借助当今的计算机图形工具,我们还是可以把它可视化的。 看一下混叠在频域是什么样的 贴一下不好理解的数学推导首先对于连续时域信号\(g_a(t)\),我们对它进行时域采样得\(g_p(t)\) ,即 \[p(t)=\sum_{n=-\infty}^{+\infty} \delta(t-n T)\tag{2} \]\[g_{p}(t)=g_{a}(t) p(t)=\sum_{n=-\infty}^{\infty} g_{a}(n T) \delta(t-n T) \tag{3} \]根据CTFT(连续时间傅里叶变换),得 \[\begin{aligned} &G_{p}(j \Omega)=\int_{-\infty}^{\infty} g_{p}(t) e^{-j \Omega t} d t \\ &=\int_{-\infty}^{\infty}\left[\sum_{n=-\infty}^{\infty} g_{a}(n T) \delta(t-n T)\right] e^{-j \Omega t} d t \\ &=\sum_{n=-\infty}^{\infty} g_{a}(n T) e^{-j \Omega n T} \int_{-\infty}^{\infty} \delta(t-n T) d t \\ &=\sum_{n=-\infty}^{\infty} g_{a}(n T) e^{-j \Omega n T} \end{aligned}\tag{4} \]对照DTFT(离散时间傅里叶变换)的公式 \[G\left(e^{j \omega}\right)=\sum_{n=-\infty}^{\infty} g[n] e^{-j \omega n}\tag{5} \]得, \(G_{p}(j \Omega)\)和\(G\left(e^{j \omega}\right)\)的关系 \[G_{p}(j \Omega)=\left.G\left(e^{j \omega}\right)\right|_{\omega=\Omega T}\tag{6} \]\(p(t)\)的傅里叶级数展开 \[p(t)=\frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j(2 \pi / T) k t}=\frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j \Omega_{T} k t}\tag{7} \]由\((3)\)得\(g_{p}(t)\) \[g_{p}(t)=\left(\frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j \Omega_{T} k t}\right) \cdot g_{a}(t)\\ =\frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j \Omega_{T} k t} g_{a}(t)\tag{8} \]易得\(G_{p}(j \Omega)\)与\(G_{a}(j \Omega)\)的关系 \[G_{p}(j \Omega)=\frac{1}{T} \sum_{k=-\infty}^{\infty} G_{a}\left(j\left(\Omega-k \Omega_{T}\right)\right) \tag{9} \]另外,还可以通过CTFT的卷积性质得到(9)式 \[\begin{aligned} &g_{p}(t)=g_{a}(t) p(t) \\ &G_{p}(j \Omega)=\frac{1}{2 \pi} G_{a}(j \Omega) * P(j \Omega) \\ &\because P(j \Omega)=\frac{2 \pi}{T} \sum_{k=-\infty}^{\infty} \delta\left(\Omega-k \Omega_{T}\right) \\ &\therefore G_{p}(j \Omega)=\frac{1}{T} \sum_{k=-\infty}^{\infty} G_{a}\left(j\left(\Omega-k \Omega_{T}\right)\right) \end{aligned} \]看一下好理解的函数图像由是,当采样频率 \(\Omega_{T}>2 \Omega_{m}\)时,如下图所示
当采样频率 \(\Omega_{T} |
【本文地址】
今日新闻 |
推荐新闻 |