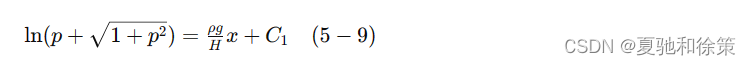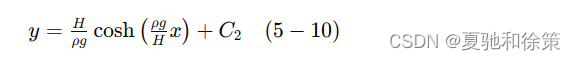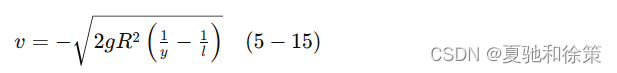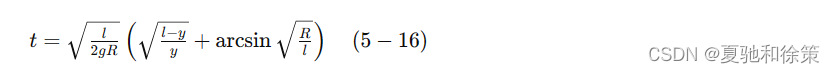第五节：可降阶的高阶微分方程

从这一节起，我们将讨论二阶及二阶以上的微分方程，即高阶微分方程。对于一些高阶微分方程，可以通过代换将其转换为较低阶的方程来求解。以二阶微分方程：

为例，如果我们能通过某种代换将其降为一阶方程，就可能使用前面章节中的方法求解。

下面介绍三种容易降阶的高阶微分方程求解方法：

形式为

的右侧只包含自变量 𝑥x，可以看出如果将 𝑦(𝑛−1)y(n−1) 作为新的未知函数，则 (5-2) 式就成为新未知函数的一阶微分方程。两边积分，可得一个 𝑛−1n−1 阶的微分方程。

依此方法继续进行，不断积分 𝑛n 次，可得 (5-2) 式的包含 𝑛n 个任意常数的通解。

例 1 求微分方程：

的通解。

解： 对所给方程连续积分三次，得：

这就是所求的通解。

例 2 质量为 𝑚m 的质点在作用力 𝐹F 下沿 𝑂𝑥Ox 轴做直线运动。设力 𝐹=𝐹(𝑡)F=F(t)，且在起始时刻 𝑡=0t=0 时 𝐹(0)=𝐹0F(0)=F0​，随着时间 𝑡t 的增长，力 𝐹F 均匀减小，直至 𝑡=𝑇t=T 时 𝐹(𝑇)=0F(T)=0。如果开始时质点位于原点，且初速度为零，求质点的运动规律。

解： 设 𝑥=𝑥(𝑡)x=x(t) 表示质点在时刻 𝑡t 时的位置，根据牛顿第二定律，质点运动的微分方程为：

由题设，力 𝐹(𝑡)F(t) 随 𝑡t 增大而均匀减小，且 𝑡=0t=0 时，𝐹(0)=𝐹0F(0)=F0​，所以：

又在 𝑡=𝑇t=T 时，𝐹(𝑇)=0F(T)=0，因此方程 (5-3) 可以写成：

其初值条件为：

把 (5-4) 式两端积分，得到：

根据初值条件 𝑑𝑥𝑑𝑡(0)=0dtdx​(0)=0，得：

𝐶1=0C1​=0

于是 (5-5) 式成为：

𝑚𝑑𝑥𝑑𝑡=𝐹0(−𝑡22𝑇+𝑡)mdtdx​=F0​(−2Tt2​+t)

把 (5-5) 式再次积分，得到：

根据初值条件 𝑥(0)=0x(0)=0，得：

𝐶2=0C2​=0

于是所求质点的运动规律为：

方程：

的右侧并不显式包含未知函数 𝑦y。如果我们设 𝑦′=𝑝y′=p，那么：

方程 (5-7) 就变为：

这是一个关于变量 𝑥x 和 𝑝p 的一阶微分方程。设其通解为：

于是得到另一个一阶微分方程：

𝑑𝑦𝑑𝑥=𝑔(𝑥,𝐶)dxdy​=g(x,C)

对其进行积分，即可得方程 (5-7) 的通解：

例 3 求解微分方程：

(1+𝑥2)𝑦′′=2𝑥𝑦′(1+x2)y′′=2xy′

并满足初值条件：

𝑦(0)=1,𝑦′(0)=3y(0)=1,y′(0)=3

的特解。

解： 所给方程是 𝑦′′=𝑓(𝑥,𝑦′)y′′=f(x,y′) 型的。设 𝑦′=𝑝y′=p，代入方程并分离变量后，有：

两端积分得：

即：

𝑝=𝑦′=𝐶1(1+𝑥2)(𝐶1=±𝑒𝐶1)p=y′=C1​(1+x2)(C1​=±eC1​)

根据条件 𝑦′(0)=3y′(0)=3，得：

𝐶1=3C1​=3

所以：

𝑦′=3(1+𝑥2)y′=3(1+x2)

两端再积分得：

𝑦=𝑥3+3𝑥+𝐶2y=x3+3x+C2​

根据条件 𝑦(0)=1y(0)=1，得：

𝐶2=1C2​=1

于是所求的特解为：

例 4 设有一均匀、柔软的绳索，两端固定，绳索仅受重力作用而下垂。试问该绳索在平衡状态时是怎样的曲线？

解： 设绳索的最低点为 A。取 y 轴通过 A 点铅直向上，x 轴水平向右。假设 OA 的长度等于某个定值（这个定值将在以后确定）。设绳索的曲线方程为 𝑦=𝜙(𝑥)y=ϕ(x)。考察从 A 点到另一点 M(x, y) 之间的弧 AM，设其长为 𝑠s。

假定绳索的线密度为 𝜌ρ，则弧 AM 所受的重力为 𝜌𝑔𝑠ρgs。由于绳索是柔软的，在 A 点的张力沿水平方向，其大小为 H；在 M 点的张力沿该点的切线方向，设其倾角为 𝜃θ，大小为 T（见图 7-6）。

根据平衡条件，将弧段 AM 上的力分解到水平和铅直两个方向，得：

将这两式相除，得到：

由于 tan⁡𝜃=𝑦′tanθ=y′，且 𝑠=∫1+(𝑦′)2 𝑑𝑥s=∫1+(y′)2​dx，代入上式即得：

将上式两端对 x 求导，得到方程：

设原点 O 到 A 点的距离为定值 𝑎a，即 ∣𝑂𝐴∣=𝑎∣OA∣=a，其初值条件为：

𝑦(0)=𝑎,𝑦′(0)=0y(0)=a,y′(0)=0

下面来求解方程 (5-8)。

该方程属于 𝑦′′=𝑓(𝑥,𝑦′)y′′=f(x,y′) 类型。设 𝑦′=𝑝y′=p，代入方程 (5-8)，并分离变量，得到：

两端积分得：

根据条件 𝑦′(0)=𝑝=0y′(0)=p=0，得：

𝐶1=0C1​=0

于是 (5-9) 式成为：

解得：

𝑝=𝑦′=𝐻𝜌𝑔sinh⁡(𝜌𝑔𝐻𝑥)p=y′=ρgH​sinh(Hρg​x)

因此：

根据条件 𝑦(0)=𝑎y(0)=a，得：

𝐶2=−𝐻𝜌𝑔C2​=−ρgH​

于是该绳索的形状可以由曲线方程：

表示。这条曲线被称为悬链线。

对于方程：

右端不显式包含自变量 𝑥x。为了求解它的解，我们设 𝑦′=𝑝y′=p，并利用复合函数的求导法则将 𝑦′′y′′ 转化为对 𝑦y 的导数：

于是方程 (5-11) 变成：

这是一个关于变量 𝑦y 和 𝑝p 的一阶微分方程。设其通解为：

分离变量并积分，即可得方程 (5-11) 的通解：

例 5 求解微分方程：

解： 方程 (5-12) 的右端不显含自变量 𝑥x，设 𝑦′=𝑝y′=p，那么 𝑦=∫𝑝 𝑑𝑥y=∫pdx。代入方程 (5-12) 得：

在 𝑦≠0y=0 且 𝑝≠0p=0 时，约去 𝑝p，并分离变量，得：

𝑑𝑝𝑝=𝑑𝑦𝑦pdp​=ydy​

两端积分得：

即：

𝑝=𝐶1𝑦(𝐶1=±𝑒𝐶1)p=C1​y(C1​=±eC1​)

分离变量并两端积分，即可得方程 (5-12) 的通解：

ln⁡∣𝑦∣=𝐶1𝑥+𝐶2ln∣y∣=C1​x+C2​

或者：

例 6 一个离地面很高的物体，在地球引力作用下从静止开始自由下落。求它到达地面时的速度和所需的时间（不计空气阻力）。

解： 取连接地球中心与物体的直线为 y 轴，方向垂直向上，并以地球的中心为原点 O。设地球半径为 R，物体质量为 m，物体开始下落时与地球中心的距离为 𝑙l（𝑙>𝑅l>R），在时刻 𝑡t 时物体的位置为 𝑦(𝑡)y(t)，速度为 𝑣=𝑑𝑦𝑑𝑡v=dtdy​。

根据万有引力定律，得到微分方程：

其中，M 为地球的质量，G 为引力常数。由于当 𝑦=𝑅y=R 时，重力加速度 𝑔=𝐺𝑀𝑅2g=R2GM​，所以：

𝐺𝑀=𝑔𝑅2GM=gR2

于是方程 (5-13) 成为：

初始条件为：

我们先求物体到达地面时的速度。将：

代入方程 (5-14) 并分离变量，得：

在 (5-15) 式中令 𝑦=𝑅y=R，得到物体到达地面时的速度为：

我们接下来求物体落到地面所需的时间。由 (5-15) 式可得：

分离变量并对两端积分（对右端积分使用替换 𝑦=𝑙cos⁡2𝑢y=lcos2u），得到：

由初始条件 𝑦(0)=𝑙y(0)=l 可得 𝐶2=0C2​=0。

于是 (5-16) 式成为：

这就是物体到达地面所需的时间。