PyTorch 中 torch.matmul() 函数的文档详解 |
您所在的位置:网站首页 › 张量运算法则 › PyTorch 中 torch.matmul() 函数的文档详解 |
PyTorch 中 torch.matmul() 函数的文档详解
|
官方文档
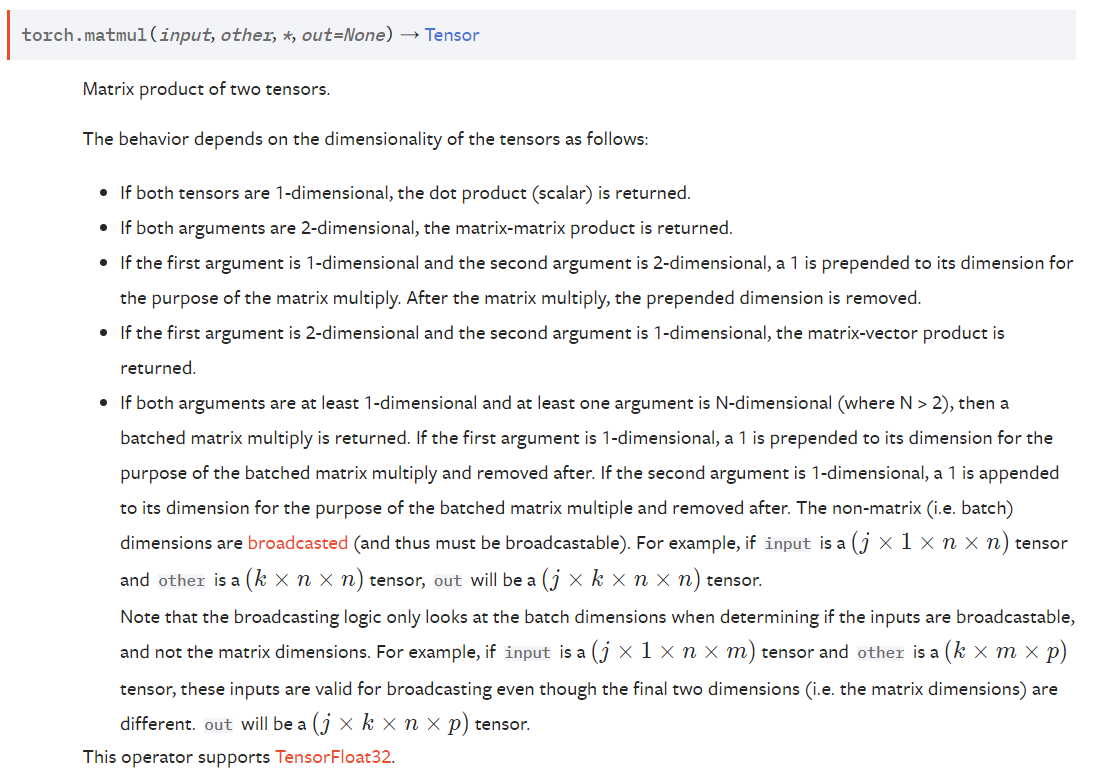
torch.matmul() 函数几乎可以用于所有矩阵/向量相乘的情况,其乘法规则视参与乘法的两个张量的维度而定。 关于 PyTorch 中的其他乘法函数可以看这篇博文,有助于下面各种乘法的理解。 torch.matmul() 将两个张量相乘划分成了五种情形:一维 × 一维、二维 × 二维、一维 × 二维、二维 × 一维、涉及到三维及三维以上维度的张量的乘法。 以下是五种情形的详细解释: 如果两个张量都是一维的,即 torch.Size([n]) ,此时返回两个向量的点积。作用与 torch.dot() 相同,同样要求两个一维张量的元素个数相同。 例如: >>> vec1 = torch.tensor([1, 2, 3]) >>> vec2 = torch.tensor([2, 3, 4]) >>> torch.matmul(vec1, vec2) tensor(20) >>> torch.dot(vec1, vec2) tensor(20) # 两个一维张量的元素个数要相同! >>> vec1 = torch.tensor([1, 2, 3]) >>> vec2 = torch.tensor([2, 3, 4, 5]) >>> torch.matmul(vec1, vec2) Traceback (most recent call last): File "", line 1, in RuntimeError: inconsistent tensor size, expected tensor [3] and src [4] to have the same number of elements, but got 3 and 4 elements respectively如果两个参数都是二维张量,那么将返回矩阵乘积。作用与 torch.mm() 相同,同样要求两个张量的形状需要满足矩阵乘法的条件,即(n×m)×(m×p)=(n×p) 例如: >>> arg1 = torch.tensor([[1, 2], [3, 4]]) >>> arg1 tensor([[1, 2], [3, 4]]) >>> arg2 = torch.tensor([[-1], [2]]) >>> arg2 tensor([[-1], [ 2]]) >>> torch.matmul(arg1, arg2) tensor([[3], [5]]) >>> torch.mm(arg1, arg2) tensor([[3], [5]]) >>> arg2 = torch.tensor([[-1], [2], [1]]) >>> torch.matmul(arg1, arg2) # 要求满足矩阵乘法的条件 Traceback (most recent call last): File "", line 1, in RuntimeError: mat1 and mat2 shapes cannot be multiplied (2x2 and 3x1)如果第一个参数是一维张量,第二个参数是二维张量,那么在一维张量的前面增加一个维度,然后进行矩阵乘法,矩阵乘法结束后移除添加的维度。文档原文为:“a 1 is prepended to its dimension for the purpose of the matrix multiply. After the matrix multiply, the prepended dimension is removed.” 例如: >>> arg1 = torch.tensor([-1, 2]) >>> arg2 = torch.tensor([[1, 2], [3, 4]]) >>> torch.matmul(arg1, arg2) tensor([5, 6]) >>> arg1 = torch.unsqueeze(arg1, 0) # 在一维张量前增加一个维度 >>> arg1.shape torch.Size([1, 2]) >>> ans = torch.mm(arg1, arg2) # 进行矩阵乘法 >>> ans tensor([[5, 6]]) >>> ans = torch.squeeze(ans, 0) # 移除增加的维度 >>> ans tensor([5, 6])如果第一个参数是二维张量(矩阵),第二个参数是一维张量(向量),那么将返回矩阵×向量的积。作用与 torch.mv() 相同。另外要求矩阵的形状和向量的形状满足矩阵乘法的要求。 例如: >>> arg1 = torch.tensor([[1, 2], [3, 4]]) >>> arg2 = torch.tensor([-1, 2]) >>> torch.matmul(arg1, arg2) tensor([3, 5]) >>> torch.mv(arg1, arg2) tensor([3, 5])如果两个参数均至少为一维,且其中一个参数的 ndim > 2,那么……(一番处理),然后进行批量矩阵乘法。 这条规则将所有涉及到三维张量及三维以上的张量(下文称为高维张量)的乘法分为三类:一维张量 × 高维张量、高维张量 × 一维张量、二维及二维以上的张量 × 二维及二维以上的张量。 如果第一个参数是一维张量,那么在此张量之前增加一个维度。 文档原文为:“ If the first argument is 1-dimensional, a 1 is prepended to its dimension for the purpose of the batched matrix multiply and removed after.” 如果第二个参数是一维张量,那么在此张量之后增加一个维度。 文档原文为:“If the second argument is 1-dimensional, a 1 is appended to its dimension for the purpose of the batched matrix multiple and removed after. ” 由于上述两个规则,所有涉及到一维张量和高维张量的乘法都被转变为二维及二维以上的张量 × 二维及二维以上的张量。 然后除掉最右边的两个维度,对剩下的维度进行广播。原文为:“The non-matrix dimensions are broadcasted.” 然后就可以进行批量矩阵乘法。 For example, if input is a (j × 1 × n × n) tensor and other is a (k × n × n) tensor, out will be a (j × k × n × n) tensor. 举例如下: >>> arg1 = torch.tensor([1, 2, -1, 1]) >>> arg2 = torch.randint(low=-2, high=3, size=[3, 4, 1]) >>> torch.matmul(arg1, arg2) tensor([[ 5], [-1], [-1]]) >>> arg2 tensor([[[ 2], [ 2], [-1], [-2]], [[-2], [ 2], [ 1], [-2]], [[ 0], [ 0], [-1], [-2]]])根据第一条规则,先对 arg1 增加维度: >>> arg3 = torch.unsqueeze(arg1, 0) >>> arg3 tensor([[ 1, 2, -1, 1]]) >>> arg3.shape torch.Size([1, 4])由于 arg2.shape=torch.Size([3, 4, 1]) ,根据广播的规则,arg3 要被广播为 torch.Size([3, 1, 4]) ,也就是下面的 arg4。 >>> arg4 = torch.tensor([ [[ 1, 2, -1, 1]], [[ 1, 2, -1, 1]], [[ 1, 2, -1, 1]] ]) >>> arg4 tensor([[[ 1, 2, -1, 1]], [[ 1, 2, -1, 1]], [[ 1, 2, -1, 1]]]) >>> arg4.shape torch.Size([3, 1, 4])最后我们使用乘法函数 torch.bmm() 来进行批量矩阵乘法: >>> torch.bmm(arg4, arg2) tensor([[[ 5]], [[-1]], [[-1]]])由于在第一条规则中对一维张量增加了维度,因此矩阵计算结束后要移除这个维度。移除之后和前面使用 torch.matmul() 的结果相同! PS:在看文档第五条规则时,起先也非常不明白,试了很多次高维和一维的张量乘法总是提示RuntimeError: mat1 and mat2 shapes cannot be multiplied,然后就尝试理解这条规则。因为这条规则很长,分成了三个小情形,并且这三个情形并不是一一独立的,而是前两个情形经过处理之后最后全都可以转变成第三个情形。另一个理解的突破口是 prepended 和 appended 这两个单词,通过它们的前缀可以猜测出:一个是在张量前面增加维度,一个是在张量后面增加维度,然后广播再进行批量矩阵乘法就验证出来了! |
【本文地址】