线性规划(Linear Programming)是运筹学中数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出求解线性规划的单纯形法以来，线性规划在理论上趋向成熟，在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划变成现代管理中经常采用的基本方法之一。 在解决实际问题时，需要把问题归结成一个线性规划数学模型，关键及难点在于选适当的决策变量建立恰当的模型，这直接影响到问题的求解。

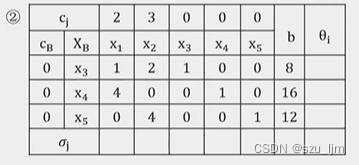
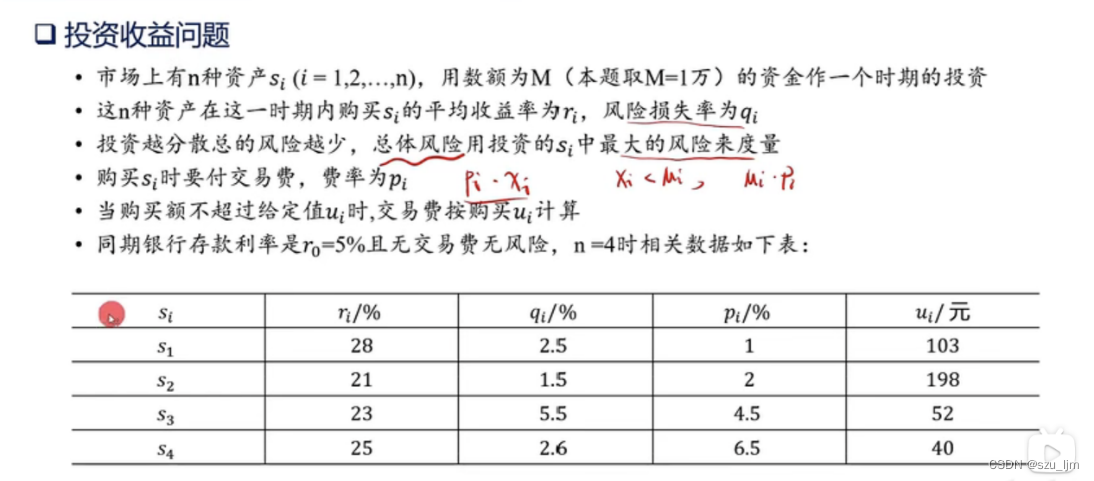
单纯形法是求解线性规划问题最常用、最有效的算法之一。满足线性规划问题约束条件的所有点组成的集合就是线性规划的可行域，单纯形法的基本想法是从线性规划可行域的某一个顶点出发，沿着使目标函数值下降的方向寻求下一个顶点，面顶点个数是有限的，所以，只要这个线性规划有最优解，那么通过有限步迭代后，必可求出最优解。

为了用迭代法求出线性规划的最优解，需要解决以下三个问题 ：

最优解判别准则，即迭代终止的判别标准

换基运算，即从一个基可行解迭代出另一个基可行解的方法

进基列的选择，即选择合适的列以进行换基运算，可以使目标函数值有较大下降 。

简单来说，我们根据标准化后的线性方程组构建单纯形表，通过一些矩阵变换处理后，判断检验数的正负，若全部检验数小于等于0则表示此时求出的解即为最优解，否则不是最优解。若不是最优解的话要重新选取新的基变量，迭代到最终满足所有的检验数均不大于0

数学推导详见该博客

拿到一道可以用线性规划来解决的问题，首先我们要明确线性规划的几大要素：决策变量，目标函数，约束条件，特别是当条件和问题多起来后不进行清晰的要素分析会很容易出错，下面假设有一道投资和最大收益的问题

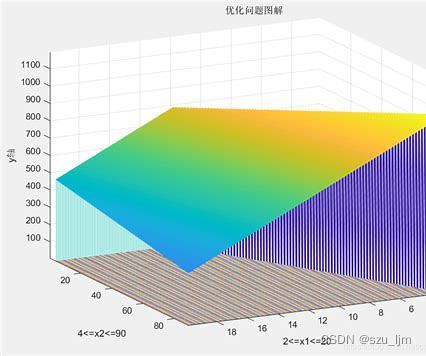
对于上述问题，我们的目标函数是使得收益最大化并且总体风险最小化，在投资资产一定的情况下，总收益就却取决于每种资产的投资金额、收益率和费率，总风险就取决于每种资产的投资金额、投资资产种类数和损失率。但为了简化模型的需要，我们可以将总风险最小化转化为针对不同人群的最小风险率，即该人群可以接受的最大损失。

决策变量主要是每种资产的投资金额，因为每类投资的收益率、费率、损失率都是一定的，我们也通过转化将目标函数转化为约束条件，最终约束条件是总投资金额为定值，每类投资的金额都为正值，总风险率低于某个定值

我们假设总收益函数为 Q Q Q，每个项目投资的资金为 X i X_{i} Xi​，每个项目的平均收益率为 r i r_{i} ri​，每个项目的平均风险损失率为 q i q_{i} qi​，每个项目的费率为 p i p_{i} pi​，还有我们在模型假设是可以说明投资金额 M M M 远大于 u i u_{i} ui​来规避分类讨论的情形，下面是目标函数的表达式

max ⁡ Q = max ⁡ ∑ i = 0 4 ( r i − p i ) X i \max Q = \max \sum_{i=0}^4 (r_{i} - p_{i}) X_{i} maxQ=maxi=0∑4​(ri​−pi​)Xi​

下面是几个约束条件的数学表达式，其中最小风险率我们用平均损失率和每类项目的投资金额的乘积和总投资金额的比来衡量

q i X i M < = a ， a 为某个特定的最小风险率 \frac{q_{i} X_{i}}{M} = 0 , i=0,1,2,3,4 Xi​>=0,i=0,1,2,3,4

上面就是我们简化后的数学模型，如果不对模型进行简化将总风险最小化的目标函数转化风险率小于某个值，我们就要解决表达式 min ⁡ ( max ⁡ 1 < = i < = 4 ( q i X i ) ) \min{(\max_{1'type': 'ineq', 'fun': lambda x: -x[1] - x[3] - x[5] - x[7] - x[9] - x[11] + b2}, \ {'type': 'eq', 'fun': lambda x: -x[0] - x[1] + d1}, \ {'type': 'eq', 'fun': lambda x: -x[2] - x[3] + d2}, \ {'type': 'eq', 'fun': lambda x: -x[4] - x[5] + d3}, \ {'type': 'eq', 'fun': lambda x: -x[6] - x[7] + d4}, \ {'type': 'eq', 'fun': lambda x: -x[8] - x[9] + d5}, \ {'type': 'eq', 'fun': lambda x: -x[10] - x[11] + d6}) return cons cons = con(args2) #设置初始预测值 x0 = np.array([1, 2, 1, 4, 1, 3, 1, 6, 1, 5, 1, 10, 3, 3, 5, 5]) # 计算 solution = minimize(objective(args1), x0, method='SLSQP', constraints=cons) x = solution.x print(solution) print('\n') print('最优解 = ' + str(solution.fun)) print('料场1横坐标 = ' + str(x[12])) print('料场1纵坐标 = ' + str(x[13])) print('料场2横坐标 = ' + str(x[14])) print('料场2纵坐标 = ' + str(x[15])) #/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code6.py message: Inequality constraints incompatible success: False status: 4 fun: -8330466284030726.0 x: [-4.565e+04 4.565e+04 ... 3.222e+05 -2.365e+04] nit: 4 jac: [ 3.355e+08 0.000e+00 ... -5.161e+10 0.000e+00] nfev: 68 njev: 4 最优解 = -8330466284030726.0 料场1横坐标 = -24603.887006224133 料场1纵坐标 = -7864.964381965315 料场2横坐标 = 322189.52738244593 料场2纵坐标 = -23652.50564799086 #Process finished with exit code 0 总结

以上就是今天笔记的内容，本文简单介绍了线性规划和非线性规划的总体实现思路和求解方法，线性规划和非线性规划在数学建模和机器学习中被广泛地应用，特别适合一些最优化方案的求解，线性规划和非线性规划的模型也有自身的局限性，总之善于利用不同模型的优势才能更加彻底的剖析事物背后的数学逻辑。