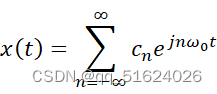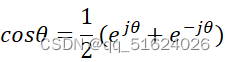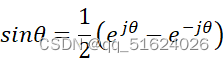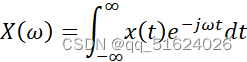一、傅里叶变换的理论基础

傅里叶变换是一种将一个信号分解成不同频率的正弦和余弦信号的数学工具。它的理论基础是傅里叶级数，傅里叶级数是指将周期信号分解成一组正弦和余弦函数的和。傅里叶级数的表达式为：

xt=n=-∞∞cnejnω0t

其中，x(t)为周期为T的信号，cn为信号的傅里叶系数，ω0=2π/T为基本角频率。傅里叶级数的推导基于欧拉公式和复指数函数的性质。欧拉公式表达式为：

ejθ=cosθ+jsinθ

利用欧拉公式，我们可以将正弦和余弦函数表示为复指数函数的实部和虚部：

cosθ=12(ejθ+e-jθ)

sinθ=12ejθ-e-jθ

利用欧拉公式和复指数函数的性质，我们可以将周期信号表示为傅里叶级数的形式。

二、傅里叶变换的理论概述

傅里叶变换是将一个信号分解成不同频率的正弦和余弦信号的数学工具。它的表达式为：

Xω=-∞∞xte-jωtdt

其中，x(t)为信号，X(ω)为信号的傅里叶变换，ω为频率。

傅里叶变换的推导基于傅里叶级数和傅里叶积分的思想。傅里叶级数是将周期信号分解成一组正弦和余弦函数的和，而傅里叶积分是将非周期信号分解成一组连续的正弦和余弦函数的积分。傅里叶变换是傅里叶积分的推广，它可以将任意信号分解成一组离散的正弦和余弦函数的积分。傅里叶变换的物理意义是将时域信号转换为频域信号，它可以用于信号的滤波、谱分析、压缩等方面。

三、傅里叶变换的应用价值

傅里叶变换在信号处理、通信、图像处理等领域有着广泛的应用价值。

傅里叶变换可以将时域信号转换为频域信号，因此可以用于信号的滤波。通过对傅里叶变换后的频域信号进行滤波，可以去除信号中的噪声和干扰。

傅里叶变换可以将时域信号转换为频域信号，因此可以用于信号的谱分析。通过分析信号的频谱，可以了解信号的频率分布情况，从而得出信号的特征。

傅里叶变换可以将时域信号转换为频域信号，因此可以用于信号的压缩。通过保留频域信号中的主要成分，可以将信号压缩到更小的空间中，从而减小存储和传输的成本。

傅里叶变换可以将图像转换为频域信号，因此可以用于图像处理。通过对图像的傅里叶变换，可以得到图像的频域信息，从而实现图像的滤波、增强等操作。

四、傅里叶变换之间的联系和区别

傅立叶变换最早来源于连续周期信号的连续傅立叶级数（CFS），CFS仅仅针对连续、周期信号。它有两种形式，根据欧拉公式的分解与合成，可分为三角傅立叶级数和指数傅立叶级数。傅里叶级数是将周期信号分解成一组正弦和余弦函数的和。

将非周期信号看成周期信号的周期取为无穷大，就将CFS降为连续傅立叶变换(CFT)。傅里叶变换是由连续函数与离散函数的卷积定义的。由于连续函数与离散函数之间没有公共的积分路径，因此傅里叶变换只能够对连续函数进行傅里叶级数展开。

对于离散周期序列，那么它有离散傅立叶级数（DFS）。

对于离散序列，它有离散时间傅立叶变换（DTFT），特别要注意这里的DTFT中，频率属于数字角频率，和CFT中的模拟角频率是不一样的，两者关系是：数字角频=模拟角频*抽样时间。还需要注意的一点是，DTFT属于离散的时间，连续的频谱，频谱是连续的。对于由连续信号抽样得到的离散时间序列，DTFT是一个周期延拓的频谱，DTFT在一个周期内的频谱包络和CFT的频谱包络是基本一致的。

对于离散序列，它除了有DTFT，还有离散傅里叶变换（DFT），区别在于，DTFT属于时间离散，频谱连续，而DFT则是时间离散，频谱也是离散的，所以DFT本质上是对DTFT在频域上均匀采样。并且DFT是DFS的单周期主值，也即是将非周期序列周期延拓后的周期信号的DFS的单周期主值。用离散时间信号和连续时间信号分别描述离散时间系统，就是最常见的两种方式。比如我们学习过的，我们平时所熟悉的模拟电子技术、自动控制技术、语音技术等则属于离散时间系统。

离散傅里叶变换DFT是数字滤波器设计的主要方法之一，它以无限长周期为条件，计算出一个数字滤波器的设计系数，并由这个系数决定它所需要的频率响应。DFT的基本思想是先利用有限长周期信号的傅里叶级数近似公式，将无限长周期信号分解成有限个周期信号的乘积。然后对每个周期信号进行卷积运算，即得到滤波器设计系数。利用无限长周期信号来设计滤波器是非常方便的，但对有限长周期信号则要考虑如何将其转化为无限短周期的问题。采用有限长周期信号来计算滤波器通带内响应和阻带内响应可以避免无限短周期的问题，但由于采用了无限长周期信号作为滤波器的设计系数，使其计算量大增。这就是DFT技术在滤波器设计中应用的局限性。

对于离散序列，其DFT的快速算法称之为FFT，由于DFT采用矩阵相乘，算法复杂度为信号规模的平方，而FFT有效利用了旋转因子的对称性，很好地降低了DFT的复杂度。FFT有时间抽取（DIT）和频率抽取(DIF)两种。

对于离散序列的z变换，如果将z用ejω做变量替换，则z变换退化为DTFT。在具体应用中需要根据信号的特点选择合适的傅里叶变换形式。

傅里叶级数和傅里叶变换是连续的数学工具，而离散傅里叶变换是离散的数学工具。因此，离散傅里叶变换只能处理离散信号，而傅里叶级数和傅里叶变换可以处理连续信号和离散信号。

傅里叶级数、傅里叶变换和离散傅里叶变换都具有反变换，可以将频域信号转换回时域信号。傅里叶级数和傅里叶变换的反变换是积分形式，而离散傅里叶变换的反变换是离散形式。

傅里叶级数、傅里叶变换和离散傅里叶变换都具有对称性和线性性质。对称性质指的是，信号的傅里叶变换或离散傅里叶变换的实部和虚部具有对称性。线性性质指的是，信号的傅里叶变换或离散傅里叶变换可以通过线性组合来表示。

傅里叶级数、傅里叶变换和离散傅里叶变换的计算复杂度不同。因此，在实际应用中需要根据信号的长度和计算资源的限制选择合适的傅里叶变换形式。

五、总结

傅里叶变换是一种非常重要的数学工具，可以将信号从时域转换到频域，从而实现信号的滤波、谱分析、压缩等操作。傅里叶变换有多种形式，包括傅里叶级数、傅里叶变换、离散傅里叶变换等，它们之间有联系和区别。在实际应用中需要根据信号的特点选择合适的傅里叶变换形式，并根据计算资源的限制选择合适的算法。傅里叶变换的应用非常广泛，涉及到信号处理、图像处理、通信等领域，是现代科学技术不可或缺的数学工具。傅里叶变换在各个领域都有应用，从数学理论角度分析，傅里叶变换是作为一个数学工具来研究信号处理和通信中信号分析与处理等问题。