常见的离散型和连续型随机变量的概率分布 |
您所在的位置:网站首页 › 常见收敛函数举例 › 常见的离散型和连续型随机变量的概率分布 |
常见的离散型和连续型随机变量的概率分布
|
目录
1 基本概念 2 离散型随机变量的概率分布 2.1 二项分布 2.2 超几何分布 2.2.1 概念 2.2.2 举例 2.3 泊松分布 3 连续型随机变量的概率分布 3.1 均匀分布 3.1.1 概念 3.2 正态分布 3.2.1 概念 3.3 指数分布 3.3.1 概念 3.3.2 举例 4 参考文献 1 基本概念在之前的博文中,已经明白了概率分布函数和概率密度函数。下面来讲解一下常见的离散型和连续型随机变量概率分布。 在此之前,介绍几个基本概念: 均值(期望值expected value):其中,可以证明 如果进行n次不同的实验,每次试验完全相同并且只有两种可能的结果,这样的实验结果分布情况就是二项分布。最简单的比如投掷一枚硬币,不管进行多少次实验,实验结果都只有正面朝上或者反面朝上,这就是一个简单的二项分布。 二项分布概率分布: 其中:n代表n次实验,x表示实验结果为T的次数,q是实验结果为T的概率,q=1-p,表示实验结果为F的概率。 二项分布的 均值: 超几何分布和二项分布比较相似,二项分布每次实验完全一样,而超几何分布前一次的实验结果会影响后面的实验结果。简单地讲,二项分布抽取之后放回元素,而超几何分布是无放回的抽取。 超几何分布的概率分布,均值和方差 在一个口袋中装有30个球,其中有10个红球,其余为白球,这些球除颜色外完全相同。游戏者一次从中摸出5个球。摸到至少4个红球就中一等奖,那么获一等奖的概率是多少? 解:由题意可见此问题归结为超几何分布模型。 其中N = 30. r = 10. n = 5. P(一等奖)= P(X=4)+ P(X=5) 由公式 ,x=0,1,2,...得:
P(一等奖) = 106/3393 2.3 泊松分布2.3.1 概念 泊松分布适合于描述单位时间内随机事件发生的次数。泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数,一块产品上的缺陷数,显微镜下单位分区内的细菌分布数等等。 泊松分布的概率分布,均值和方差: 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。 2.3.2 举例 采用0.05J/㎡紫外线照射大肠杆菌时,每个基因组平均产生3个嘧啶二体。实际上每个基因组二体的分布是服从泊松分布的,将取如下形式:
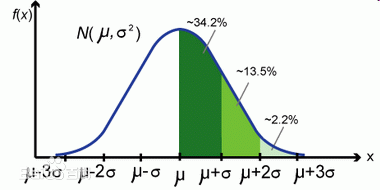
…… 3 连续型随机变量的概率分布 3.1 均匀分布 3.1.1 概念均匀概率分布(uniform probability distribution)是指连续随机变量所有可能出现值出现概率都相同。 均值: 方差: 如何求解均值和标准差: 正态分布是统计学中常见的一种分布,表现为两边对称,是一种钟型的概率分布(bell curve),其概率密度图为: 概率密度函数为:
其中, 特别的,当
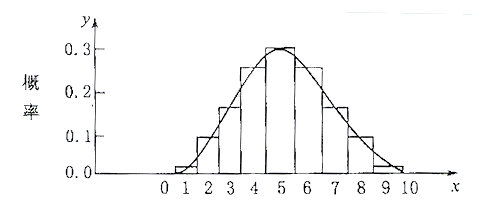
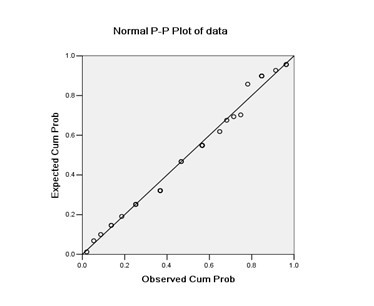
正态分布转化为标准正态分布: 正态分布x,均值是μ,标准差是σ,z定义为 正态分布来近似二项分布 : 当n足够大的时候,正态分布对于离散型二项分布能够很好地近似。 评价正态分布 : 如何来确定数据是否正态分布,主要有以下几种方法: 1. 图形感受法:建立直方图或者枝干图,看图像的形状是否类似正态曲线,既土墩形或者钟形,并且两端对称。 2. 计算区间 指数分布是描述泊松分布中事件发生时间间隔的概率分布。除了用于泊松过程的分析,还有许多其他应用,如以下场景: 世界杯比赛中进球之间的时间间隔超市客户中心接到顾客来电之间的时间间隔流星雨发生的时间间隔机器发生故障之间的时间间隔癌症病人从确诊到死亡的时间间隔 指数分布有如下的适用条件: 1. x是两个事件发生之间的时间间隔,并且x>0; 2. 事件之间是相互独立的; 3. 事件发生的频率是稳定的; 4. 两个事件不能发生在同一瞬间。 这几个条件实质上也是使用泊松分布的前提条件。如果满足上述条件,则x是一个指数随机变量,x的分布是一个指数分布。如果不满足上述条件,那么需要使用Weibull分布或者gamma分布。 指数分布只有一个参数,“λ”,λ是事件发生的频率,在不同的应用场景中可能有不同名称: 事件频率到达频率死亡率故障率转变率…………λ是单元时间内事件发生的次数,这里需要注意的是,单元时间可以是秒,分,小时等不同的单位,同时λ根据单元时间度量的不同,其数值也不一样。如单元时间为1小时,λ为6,则单元时间1分钟,λ为6/60=0.1 指数分布的概率密度函数(probability density func,PDF)由λ和x(时间)构成: 均值: 方差: 一个设备出现多次故障的时间间隔记录如下: 23, 261, 87, 7, 120, 14, 62, 47, 225, 71, 246, 21, 42, 20, 5, 12, 120, 11, 3, 14, 71, 11, 14, 11, 16, 90, 1, 16, 52, 95 根据上面数据,我们可以计算得到该设备发生故障的平均时间是59.6小时,即单位小时时间内发生故障事件的次数为λ=1/59.6=0.0168。 那么该设备在3天(72小时)内出现故障的概率是多大呢?即求P(x |
【本文地址】

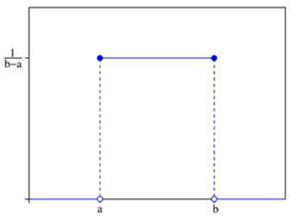 均匀分布的概率分布,均值,方差和标准差:
均匀分布的概率分布,均值,方差和标准差: