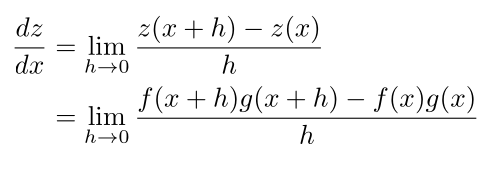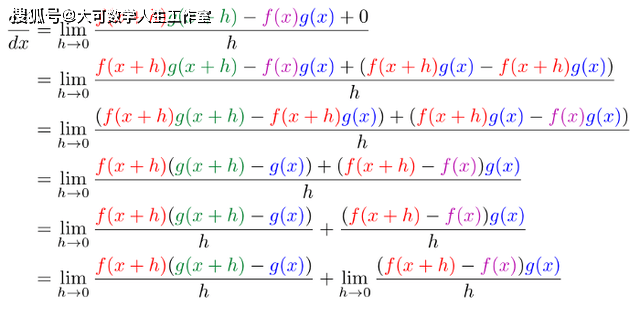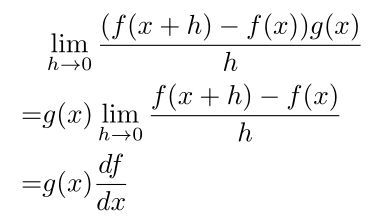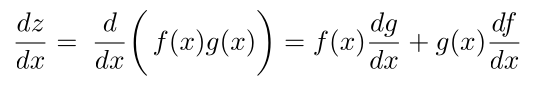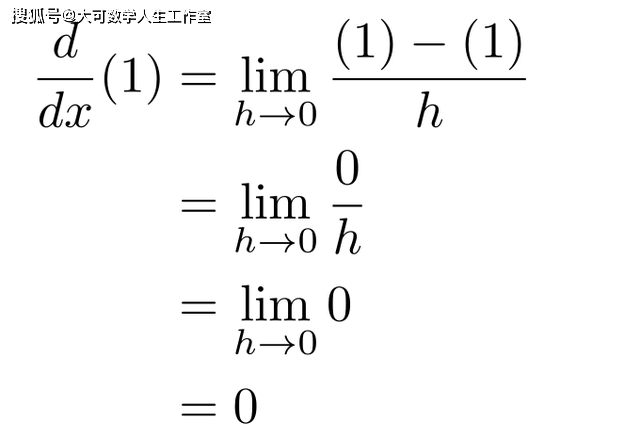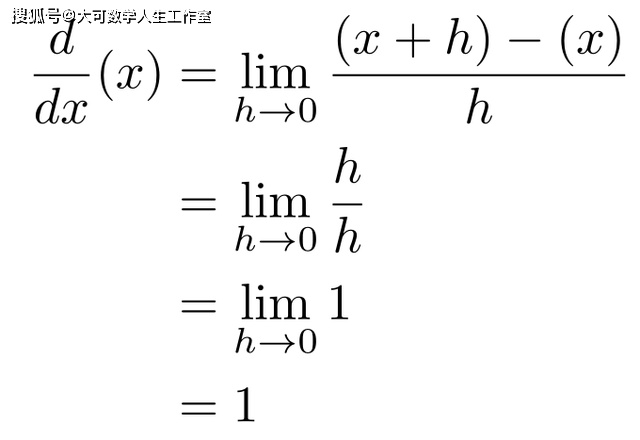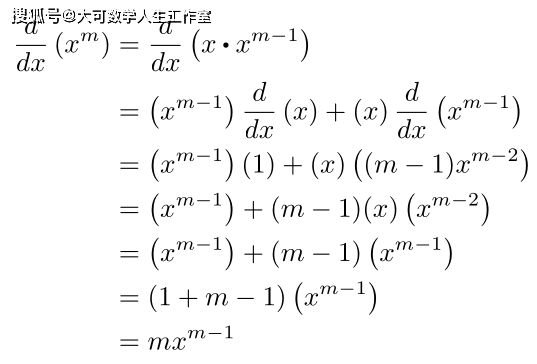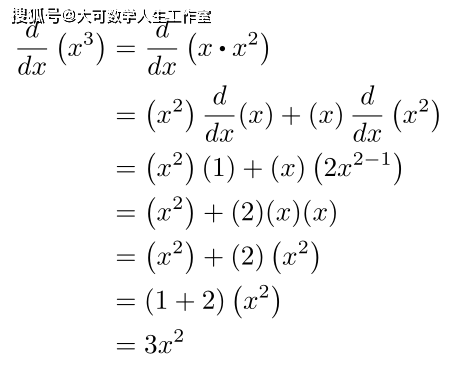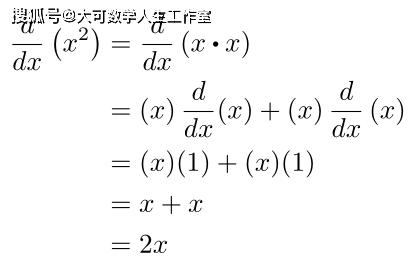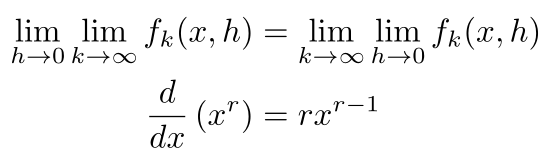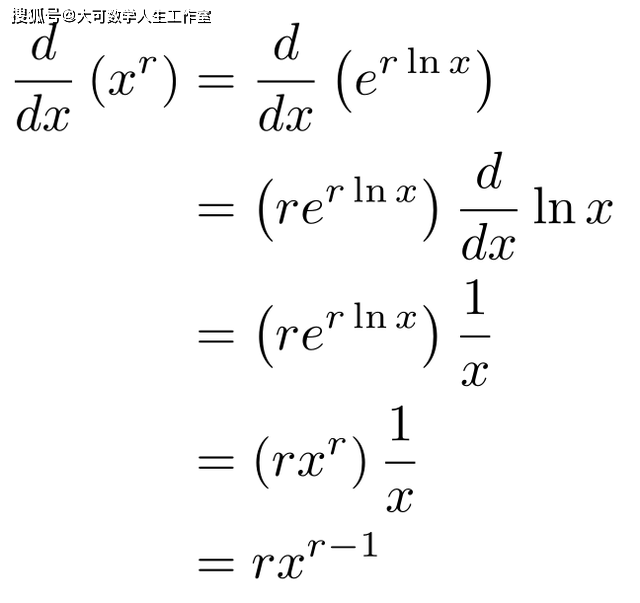积法则（The Product Rule）

我们知道， x^4= x x^3。如果我们知道如何求x和x^3的导数，以及两个函数的乘积的导数，我们就可以求x的导数。出于这个原因，我们将证明积法则。

我们要从导数的定义来证明积法则。首先，定义一个函数z(x)=f(x)g(x)。然后，z相对于x的导数。由于我们谈论的是任意函数，我们必须使用导数的定义。

可能没有什么能让你眼前一亮，在这种情况下，我们要寻找一些方法，以不同的形式重写表达式。既然表达式中有一个f(x+h)和一个g(x+h)，我们就应该设法把f(x+h)-f(x)或g(x+h)-g(x)带入表达式中。这样我们就可以用导数来代替它们。在这种情况下，我们可以使用一个经典的技巧，即添加一个0。例如，我们可以把f(x+h)-f(x+h)加到分子中，这样就不会有任何变化。我们要把( f(x+h)g(x)-f(x+h)g(x))加到分子上，这时我们可以做代数：

为了让证明更容易，我将分别处理每个极限，然后把它们放回一起。第一个极限是：

第二个极限是：

因此，我们已经证明了积法则，如下图所示：

证明n是整数的情况

有三种情况：

如果我们证明每一种情况，我们就完成了这一部分。

证明n=0的情况

这就完成了证明。

证明n>0的情况

如果我们使用导数的极限定义对x、x、x……求导，你可能会看到这些导数遵循一个简单的规律：幂法则。证明n=0和n=1的情况是很简单的，因此，我们可能想尝试用归纳法证明。

归纳法的证明

要用归纳法证明什么，需要：

强归纳法和弱归纳法是等价的，但我不能在这篇文章中讨论这些细节。对于这个证明，我们要使用弱归纳法。在给你们展示了这个证明之后，我会试着给你们一个直观的感觉，为什么它是可行的。在此过程中，我将稍稍打破传统。通常，弱归纳证明指的是步骤2中的情况n和n + 1，但我将使用n - 1和n。用n + 1替换n会将表达式转换回传统形式。

基本情况

本节将很快，因为它只是代数。

归纳步骤

在证明的这一部分，我们将证明，如果幂法则在n=m-1的情况下成立，那么m的情况也成立。这一部分我选择用m而不是n，因为我已经用n表示x的幂。如果幂法则在n=m-1时不成立，那么n=m的情况是否成立就不重要了，所以我们将假设幂法则在n=m-1时成立。

归纳法的直观解释

如果你不相信这个证明是有效的，那么请选择任何一个自然数（这个证明对你选择的任何数字都有效），但我将向你展示n=3的情况，你应该看到一般的模式。首先，我已经证明了n=1的情况。现在，我将在归纳步骤中向你展示n=3这一特定情况下的证明：

如果你对n=2的情况不相信，那么我们可以重新使用归纳步骤中对n=2的特定情况的证明：

我只对n=1的情况使用了幂法则，所以你应该相信幂法则对n=3（和n=2）的情况都有效。

如果你碰巧是一个计算机科学家或程序员，你可能会认识到这是一个递归论证。在许多情况下，归纳法和递归法都可以描述一些东西，但它们会向相反的方向发展。

证明n4，fk(x)和f(x)之间的差值小于0.0001，所以N=4。我不想把一致收敛性的整个证明讲一遍，但我可以给出一般的概述：

所有无理数

现在，如果我们使用摩尔-奥斯古德定理，我们就完成了证明：

Q.E.D.

摩尔-奥斯古德定理

一方面，引用一个没有证明的定理违背了标题中的 "从0开始 "。另一方面，这篇文章是为高中到大学的学生准备的，而实际分析可能会变得相当繁琐。下面是以前的文章和接下来的计划：

结论

如果我们允许自己使用e^x和ln x的导数，我们可以使用证明：

如果我们愿意，我们可以根据e^x、ln x的定义和链式法则计算这些导数。无论哪种方式，最终都会从头证明幂法则。返回搜狐，查看更多