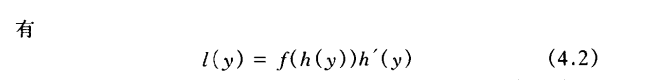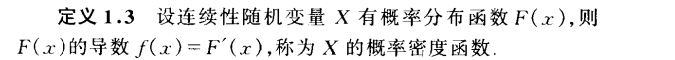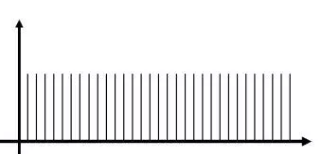
一个灰度分布不均匀的图像                                                         它的直方图

        可以看出，直方图上灰度集中在60周围，整个图像对比度较差，通过直方图均衡化，即可将其灰度均匀分布各个灰度级，从而使得图像具有更好的对比，增强图像细节。

                        均衡化后图像                                                                            均衡化后的直方图

        设随机变量x，y分别是均衡化前后的灰度取值，存在一个转换关系y=T(x)。 

        p（x），p（y）分别是x,y的概率密度函数。以p（x）为例，可以理解成，原图像灰度值是x的概率为多少。根据概率论相关知识，这里p(x)其实就是指     灰度值为x的像素数/总像素数，即该灰度值的出现概率，取值范围[0~1]，同理得p（y）。（一开始我是用f(x)，f（y)表示，为了表明它是一个概率，所以这样还是用p(x)，p(y)代替）

        p(x)是已知的。

        p(y)是直方图均衡化得到的概率密度函数，在前面我们已经说了，希望能均衡化后的直方图，拥有跟高的对比度，灰度分布更均匀，所以理想状态中的分布均匀的直方图是这样的

       这是理想中的直方图分布，这时每个灰度级的概率p=1/(L-1)，就是p(y)=1/(L-1)  L是灰度级数量，例如常用的L=256，灰度范围就是【0~255】

       我们既然希望通过x计算出形如上面灰度分布的y，就需要求T（x）这个转换关系。这样，问题转变为：

                              已知p(x)和p(y)，求T(x)。                                                                                       问题【1】

       已知两个概率密度函数p(x)，p(y)，求x，y之间的转换关系T(x)。

       这里，为了方便进行一般化情况的推导，我们将x视为一个连续的随机变量（实际上灰度值x肯定不是连续随机变量，但是为了进行公式推导和证明，先证明连续型随机变量成立，再引出离散型随机变量的情况），y就是随机变量x的函数。

        概率论里有一个小章节，叫“随机变量的函数的概率分布”，应该所有版本的概率论与数理统计都有这个内容。在这个部分所求解的问题是：               

        已知p(x)，x与y之间的转换关系T(x)，求p(y)。                                                                                          问题【2】 

这两个问题本质上都是建立的三者之间的关系，通过两个已知量即可推导第三个量。现在我们只需要去求解问题【2】，然后就可以得到三者之间的关系式，带入p(x)，p(y)就可以得到问题【1】的解。

问题【2】，p(y)证明过程，出自《概率论与数理统计》-陈希孺版：

逐步推导  ：

   x是随机变量，y=T(x)，则y是随机变量x的函数，求解随机变量函数的概率密度，一般是通过求该函数的分布函数，对

分布函数求导，得到概率密度函数。

（我去看了几个概率论的视频，老师都是说这是一般求法，我还在想为啥非得要从分布函数入手，后来贴吧大神回答说应该去看一下概率密度函数的定义，然后我看了一下书，赫然有如下定义：）

求y的分布函数F(y)，根据分布函数定义

所以F(y)=P(Y20的。因为我们必须保证，直方图均衡化后，图像的明暗关系不能改变，原本最暗的像素点，可以变亮，但是在新图像里，它也应该是相对最暗的像素点。所以T(x)必须是一个严格单调的图像（在这里进一步说，对于图像，应该是严格单调递增的。）

∵存在反函数

∴

这一步的转换，最终变成了，根据前面分布函数的定义可知，是Y的分布函数F(y），是X的分布函数，而在问题【2】的条件里，我们是不知道p(y)，更不知道F(y)的，所以才要转换成F(x)

{

这一步，通过反函数将T(X)