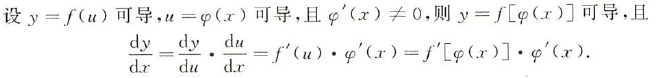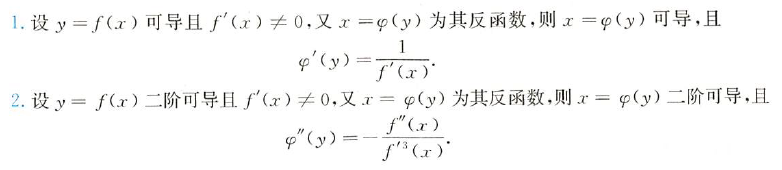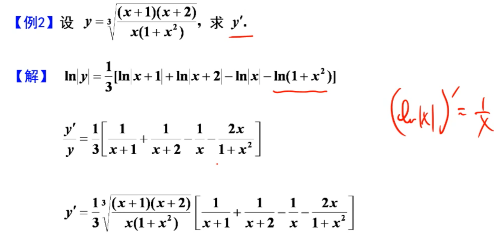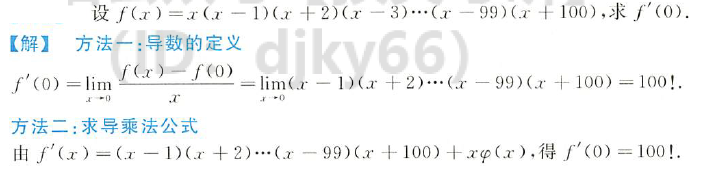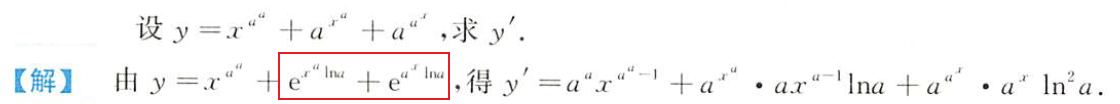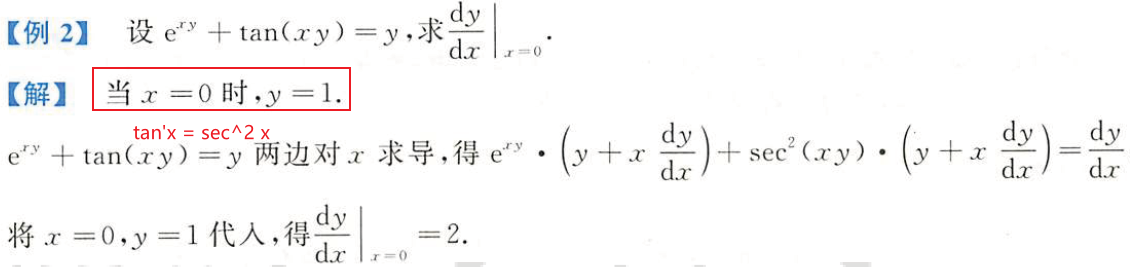导数与微分 |
您所在的位置:网站首页 › 奇函数在0点的导数存在说明什么呢对吗 › 导数与微分 |
导数与微分
|
文章目录
一 基本概念1.1 定义1.2 关系图1.3 可导条件1.4 四大性态
二 求导法则2.1 基本公式2.2 求导方法链式法则反函数求导对数求导法
2.3 高阶求导
三 隐函数3.1 定义3.2 定理3.3 参数方程求导
四 基础题型4.1 概念4.2 求导4.3 可导性
五 接力题典5.1 入门5.2 基础
一 基本概念
1.1 定义
增量 若f(x)在点x0的某个领域有定义,称 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y = {f ( x _ { 0 } + \Delta x )} - {f ( x _ { 0 } )} Δy=f(x0+Δx)−f(x0)为函数y=f(x)在x0处的增量。 导数(导数就是一个特殊的极限)
导数的定义是Δx趋于0,而不能等于0,如sin(1/x)就有等于0的点,不能作为导数定义式。 (命题点)导数的等价定义:(极限存在才能=f’(a),未说明则不能=) f ′ ( a ) = lim x → 0 f ( a + x ) − f ( a ) a + x − x = lim h → 0 f ( a + h ) − f ( a ) h = lim x → a f ( x ) − f ( a ) x − a \begin{align} f'(a) & =\lim_{x \rightarrow 0}\frac{f(a+x)-f(a)}{a+x-x} \\ & = \lim_{h \rightarrow 0}\frac{f(a+h)-f(a)}{h} \\ & = \lim_{x \rightarrow a}\frac{f(x)-f(a)}{x-a} \end{align} f′(a)=x→0lima+x−xf(a+x)−f(a)=h→0limhf(a+h)−f(a)=x→alimx−af(x)−f(a) 导数的定义是一个定点一个动点,而不能两个都是动点,如 f ( 2 x ) − f ( x ) 、 f ( x + k ) − f ( x − k ) f(2x)-f(x)、f(x+k)-f(x-k) f(2x)−f(x)、f(x+k)−f(x−k)都是两个动点,错误 可导的充要条件 函数f(x)在x=x0处可导的充要条件是左右导数存在且相等。若题目说明可导,则极限是存在的。 注解
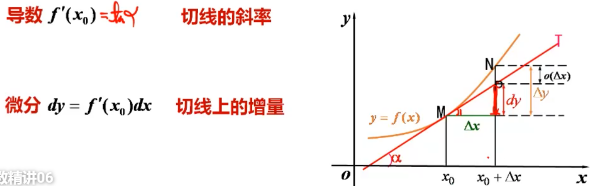
可微 增量:Δy = f(x0+Δx) - f(x0)。 若 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) \Delta y = {f ( x _ { 0 } + \Delta x )} - {f ( x _ { 0 } )} = A \Delta x + o ( \Delta x ) Δy=f(x0+Δx)−f(x0)=AΔx+o(Δx),其中A是常数,则称y=f(x)在x=x0处可微。其中AΔx称为y=f(x)在x=x0处的微分,记为dy|x=x0= AΔx = Adx Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) = d y ∣ x = x 0 + o ( Δ x ) = A d x + o ( Δ x ) = d f ( x 0 ) + o ( Δ x ) = f ′ ( x 0 ) d x + o ( Δ x ) \begin{align} Δy & = f(x_0+Δx) - f(x_0) \\ & = AΔx + o(Δx) \\ & = dy|_{x=x_0} + o(Δx) \\ & = Adx + o(Δx) \\ & = df(x_0) + o(Δx)\\ & = f'(x_0)dx + o(Δx)\\ \end{align} Δy=f(x0+Δx)−f(x0)=AΔx+o(Δx)=dy∣x=x0+o(Δx)=Adx+o(Δx)=df(x0)+o(Δx)=f′(x0)dx+o(Δx) 其他补充 对一元函数来说,可微的充要条件是可导函数的微分 与 自变量的微分 之商 等于该函数的导数,因此导数也叫微商dy = df(x) = f’(x)dx为y=f(x)的微分f(x)可导表示处处可导、f(x)连续可导表示**f’(x)**为连续函数Δx>0 情况下,f’ > 0 Δy > dy;f’ < 0 Δy < dyΔx 0 dyΔy导数与微分的关系(导数 不等于 微分)
【例题】2013数一
连续不一定可导,可导必连续。连续函数某一点可能是尖的,那就不可导。经典反例f(x)=|x|在x=0这点。
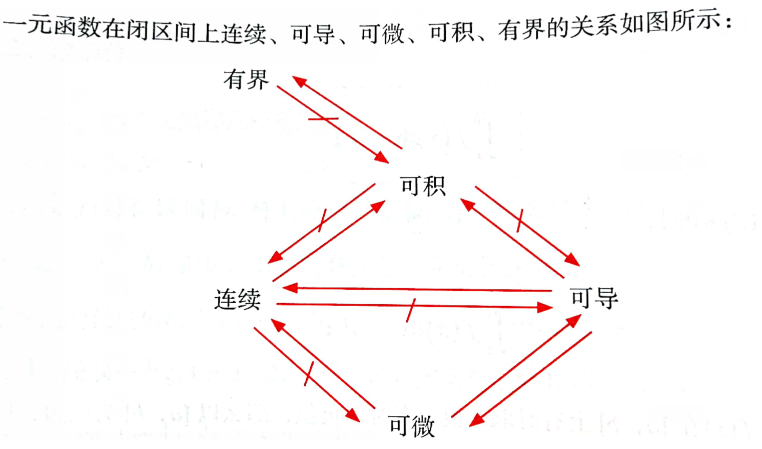
可微 > = 可导 > 连续 > 可积 > 有界 证明 一阶可导 == 可微 导->微 ∵ lim Δ x → 0 Δ y Δ x = f ′ ( a ) ∴ Δ y Δ x = f ′ ( a ) + α ( α → 0 , Δ x → 0 ) ∴ Δ y = f ′ ( a ) Δ x + α Δ x ∵ lim Δ x → 0 α Δ x Δ x = 0 ∴ α Δ x = o ( Δ x ) ∴ Δ y = f ′ ( a ) Δ x + o ( Δ x ) \begin{aligned} & \because \lim_{Δx \rightarrow0}\frac{\Delta y}{\Delta x} = f'(a) \\ & \therefore \frac{\Delta y}{\Delta x} = f'(a) + \alpha \ (\alpha \rightarrow0,\Delta x \rightarrow0) \\ & \therefore \Delta y = f'(a) \Delta x + \alpha \Delta x \\ & \because \lim_{\Delta x \rightarrow 0} \frac{\alpha \Delta x}{\Delta x} = 0 \\ & \therefore \alpha \Delta x = o(\Delta x) \\ & \therefore \Delta y = f'(a)\Delta x + o(\Delta x) \end{aligned} ∵Δx→0limΔxΔy=f′(a)∴ΔxΔy=f′(a)+α (α→0,Δx→0)∴Δy=f′(a)Δx+αΔx∵Δx→0limΔxαΔx=0∴αΔx=o(Δx)∴Δy=f′(a)Δx+o(Δx) 微->导
f(x)可导不能得出f’(x)可导,不能得出f’(x)连续、不能得出lim f’(x)存在 可导函数,导数不为0,根据介值定理知导数恒大于0或恒小于0,那么该函数单调。 1.3 可导条件证明可导性的一般步骤:先看连续不连续,不连续则必不可导;再看左右导数是否存在且相等,等则可导。注意:左右导数存在且相等,在x0点也未必可导,必须要加上连续这一条件,因为可能是跳跃间断点。 条件解析保两侧改变量Δx 要保证从两边趋于x0不可跨严格遵循导数的定义,即分子中的f(a)不能有增量阶相同分子分母中的Δ必须为同阶无穷小,如x-tan x ~ x3绝对值的可导性 设函数f(x)在x=a处可导,则|f(x)|在x=a处的可导性如下: 若 f(a) !=0,则|f(x)|在x = a处可导 若 f(a) = 0,则当f’(a) = 0 时,|f(x)|在x=a可导;当f’(a) != 0时,|f(x)|在x = a处不可导 例子:f(x) = x 与 |f(x)| 在x = 0处的可导性 一般只有一阶可导(只能保证一阶连续不能保证二阶连续)时不能洛(处处可导也不行),因为洛了之后有f’(x),要确保lim f’(x)是存在的(但一阶可导不能得出lim f’(x)存在);同理若二阶可导则可以洛一次,除非lim f’'(x)存在。即若n阶可导,至多导到n-1阶;若n阶连续可导即f(n)(x)为连续函数,最多可导到n阶。 问:为什么一阶可导不能得出lim f’(x)存在? 答:如 (sin 1/x)’ = -1/x2 cos 1/x,当x=1/nΠ 和 x=1/nΠ+0.5Π时,不等,因此极限不存在。 【例题】2018 一阶导数连续不能推出二阶导数存在、二阶可导可推出一阶连续可导 洛必达使用条件:https://mp.weixin.qq.com/s/E0KoLNOnxKoyTQz8NENJhA [例题](这里二阶能不能洛还是有点疑问,二阶连续可导不就可以洛吗?还是说这个结论错了,是至多洛到二,但存在不存在还是未知?)
单调性 f’(x0) > 0 可推出 f(x0) 单调增(只是一点),f(x0)单调增不能推出 f’(x0) >0,如x3在x=0处f’(0) = 0,但x3是单调增的。 f’(0) > 0, 根据导数的定义式,只能得出在存在δ,使得在(0,δ)中 f(x) > f(0),在(-δ,0)中f(x) < f(0),而不能证明在x=0附近单调增。即只能说明0+附近的值比f(0)大【可能振荡】,而不能说明附近的单调性。反例如下 令 f ( x ) = { x + 2 x 2 sin 1 x , x ≠ 0 0 , x = 0 则 x = 0 时 , f ′ ( 0 ) = lim x → 0 x + 2 x 2 sin 1 x x = 1 > 0 当 x ≠ 0 时 , f ′ ( x ) = 1 + 4 x sin 1 x − 2 cos 1 x f ′ ( 1 2 n π ) = − 1 < 0 \text {令} {f(x)}= \begin{cases}x+2x^{2} \sin \frac{1}{x}, & x \neq0\\0, & x=0\end{cases} \ 则\\ x=0 时, f^{\prime}(0)=\lim_{x \rightarrow0} \frac{x+2x^{2} \sin \frac{1}{x}}{x}=1>0 \\ 当x \neq0时, f^{\prime}(x)=1+4x{\text { sin } \frac{1}{x}-2\cos \frac{1}{x}} \\ f^{\prime}\left(\frac{1}{2n \pi}\right)=-10当x=0时,f′(x)=1+4x sin x1−2cosx1f′(2nπ1)=−10 推不出该点邻域单调增;因为导数在该点不一定是连续的,所以导数在邻域内可能存在负值,导致f(x)并非单调增。进一步可知f’‘(x) > 0 推不出 f(x)是凹函数,因为不能保证f’(x)是单调增。不能说明$ [\mathrm{f}(\mathrm{x}+2\Delta \mathrm{x})-\mathrm{f}(\mathrm{x}+\Delta \mathrm{x})] / \Delta \mathrm{x}>0$。 那么什么情况下才能得出单调增呢? 设f’(x)>0,若f(x)存在二阶导数,则f’(x)连续,即f‘(x)在领域内均>0,可得出f(x)单调增的结论。【一点的导数 > 0 + 该点连续 推出 邻域均 > 0】 f(x)在x==k的邻域是凹函数 不能推出 f’'(x) >0,例如x4在x=0点的二阶导为0。 有界性 若 f ( x ) ∈ C [ a , b ] {f(x)} \in C[a, b] f(x)∈C[a,b],则 f ( x ) {f(x)} f(x)在 [ a , b ] [a, b] [a,b]上一定有界 若 f ( x ) ∈ C ( a , b ) {f(x)} \in C(a, b) f(x)∈C(a,b),则 f ( x ) {f(x)} f(x)在 ( a , b ) (a, b) (a,b)上不一定有界,如1/x (命题点)若 f ( x ) ∈ C ( a , b ) {f(x)} \in C(a, b) f(x)∈C(a,b),且f(a+)存在、f(b-)存在,则 f ( x ) {f(x)} f(x)在 ( a , b ) (a, b) (a,b)上一定有界 若 f ′ ( x ) {f'(x)} f′(x)在有限区间内有界,则 f ( x ) {f(x)} f(x)在该区间内有界。反之不对如f(x)=x1/2 奇偶与周期性 ∫x0f(x)f(x)f’(x)f’'(x)f’‘’奇(下限需=0,过原点)⬅偶 ➡⬅奇➡偶➡奇➡偶(下限不影响)⬅奇 ➡偶看f(x)的积分是否==0周期 ➡周期➡周期➡周期➡周期函数的原函数是周期函数的充要条件是在其一个周期上积分为0 若 f ( x ) {f(x)} f(x)为奇函数,则 ∫ a x f ( t ) d t \int_a^x {f(t)} \mathrm{d} t ∫axf(t)dt为偶函数.若 f ( x ) {f(x)} f(x)为偶函数,则 ∫ 0 x f ( t ) d t \int_0^x {f(t)} \mathrm{d} t ∫0xf(t)dt为奇函数. 二 求导法则 2.1 基本公式(1) ( C ) ′ = 0 (C)^{\prime}=0 (C)′=0; (2) ( x α ) ′ = α x σ − 1 \left(x^{\alpha}\right)^{\prime}=\alpha x^{\sigma-1} (xα)′=αxσ−1; (3) ( a x ) ′ = a x ln a \left(a^{x}\right)^{\prime}=a^{x} \ln a (ax)′=axlna; (4) ( e x ) ′ = e x \left(\mathrm{e}^{x}\right)^{\prime}=\mathrm{e}^{x} (ex)′=ex; (5) ( log a x ) ′ = 1 x ln a \left(\log_{a} x\right)^{\prime}=\frac{1}{x \ln a} (logax)′=xlna1; (6) ( ln ∣ x ∣ ) ′ = 1 x (\ln |x|)^{\prime}=\frac{1}{x} (ln∣x∣)′=x1; (7) ( sin x ) ′ = cos x (\sin x)^{\prime}=\cos x (sinx)′=cosx; (8) ( cos x ) ′ = − sin x (\cos x)^{\prime}=-\sin x (cosx)′=−sinx; (9) ( tan x ) ′ = sec 2 x (\tan x)^{\prime}=\sec ^{2} x (tanx)′=sec2x; ( 10 ) ( cot x ) ′ = − csc 2 x (10)(\cot x)^{\prime}=-\csc ^{2} x (10)(cotx)′=−csc2x; ( 11 ) ( sec x ) ′ = sec x tan x (11)(\sec x)^{\prime}=\sec x \tan x (11)(secx)′=secxtanx; ( 12 ) ( csc x ) ′ = − csc x cot x (12)(\csc x)^{\prime}=-\csc x \cot x (12)(cscx)′=−cscxcotx; (13) ( arcsin x ) ′ = 1 1 − x 2 (\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}} (arcsinx)′=1−x2 1; (14) ( arccos x ) ′ = − 1 1 − x 2 (\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}} (arccosx)′=−1−x2 1; (15) ( arctan x ) ′ = 1 1 + x 2 (\arctan x)^{\prime}=\frac{1}{1+x^{2}} (arctanx)′=1+x21; (16) ( arccot x ) ′ = − 1 1 + x 2 (\operatorname{arccot} x)^{\prime}=-\frac{1}{1+x^{2}} (arccotx)′=−1+x21. 2.2 求导方法运算法则
证明: ∵ g ′ ( x ) = lim Δ u → 0 Δ u Δ x ≠ 0 ∴ Δ u = O ( Δ x ) ∵ f ′ ( u ) = lim Δ x → 0 Δ y Δ x ∵ d y d x = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 Δ y Δ u ∗ Δ u Δ x = lim Δ u → 0 Δ y Δ u ∗ lim Δ x → 0 Δ u Δ x = f ′ ( u ) ∗ g ′ ( x ) = f ′ ( g ( x ) ) ∗ g ′ ( x ) \begin{align} & \because g'(x) = \lim_{Δu \rightarrow0}\frac{Δu}{Δx}\neq0 \\ & \therefore Δu = O(Δx) \\ & \because f'(u) = \lim_{Δx \rightarrow0}\frac{Δy}{Δx} \\ & \because \frac{dy}{dx} = \lim_{Δx \rightarrow0}\frac{Δy}{Δx} = \lim_{Δx \rightarrow0}\frac{Δy}{Δu}*\frac{Δu}{Δx} \\ & =\lim_{Δu \rightarrow0}\frac{Δy}{Δu}*\lim_{Δx \rightarrow0}\frac{Δu}{Δx} \\ & = f'(u) * g'(x) \\ & = f'(g(x))*g'(x) \end{align} ∵g′(x)=Δu→0limΔxΔu=0∴Δu=O(Δx)∵f′(u)=Δx→0limΔxΔy∵dxdy=Δx→0limΔxΔy=Δx→0limΔuΔy∗ΔxΔu=Δu→0limΔuΔy∗Δx→0limΔxΔu=f′(u)∗g′(x)=f′(g(x))∗g′(x) 若内层函数不可导,整体函数不一定不可导。可以用定义判别 反函数求导反函数定义 y=f(x)有反函数 则必须严格单调 【保证了反函数不会出现 一对多 的情况】
求导
证明: 1 ∵ f ′ ( x ) = lim Δ x → 0 Δ y Δ x ≠ 0 ∴ g ′ ( y ) = lim Δ y → 0 Δ x Δ y = lim Δ x → 0 1 Δ y Δ x = Δ x Δ y = 1 f ′ ( x ) \begin{align} & \because f'(x) = \lim_{Δx \rightarrow0}\frac{Δy}{Δx}\neq0 \\ & \therefore g'(y) = \lim_{Δy \rightarrow0}\frac{Δx}{Δy} = \lim_{Δx \rightarrow0}\frac{1}{\frac{Δy}{Δx}} = \frac{Δx}{Δy} = \frac{1}{f'(x)} \end{align} ∵f′(x)=Δx→0limΔxΔy=0∴g′(y)=Δy→0limΔyΔx=Δx→0limΔxΔy1=ΔyΔx=f′(x)1 2 φ ′ ′ ( y ) = d d x [ 1 f ′ ( x ) ] ⋅ d x d y = − f ′ ′ ( x ) [ f ′ ( x ) ] 2 ⋅ 1 f ′ ( x ) \varphi^{\prime \prime}(y)=\frac{d}{d x}\left[\frac{1}{f^{\prime}(x)}\right] \cdot \frac{d x}{d y}=-\frac{f^{\prime \prime}(x)}{\left[f^{\prime}(x)\right]^{2}} \cdot \frac{1}{f^{\prime}(x)} φ′′(y)=dxd[f′(x)1]⋅dydx=−[f′(x)]2f′′(x)⋅f′(x)1 对数求导法
n阶导数公式 ( c a x + b ) ( n ) = c ( − 1 ) n n ! a n ( a x + b ) n + 1 ( c 为常数 ) (\frac{c}{ax+b})^{(n)} =\frac{c(-1)^nn!a^n}{(ax+b)^{n+1}} \quad (c为常数) (ax+bc)(n)=(ax+b)n+1c(−1)nn!an(c为常数) n阶三角导数公式 sin ( a x + b ) ( n ) = a n sin ( a x + n π 2 ) cos ( a + b x ) ( n ) = a n cos ( a x + n π 2 ) \sin (ax+b)^{(n)} = a^n \sin (ax+\frac{n\pi}{2}) \quad \cos (a+bx)^{(n)} = a^n \cos (ax+\frac{n\pi}{2}) \quad sin(ax+b)(n)=ansin(ax+2nπ)cos(a+bx)(n)=ancos(ax+2nπ) 复合函数 ( u v ) ( n ) = C n 0 u ( n ) v + C n 1 u ( n − 1 ) v ( 1 ) + . . . . + C n n u v ( n ) = ∑ k = 0 n C n k u ( k ) v ( n − k ) (uv)^{(n)} = C_n^{0}u^{(n)}v + C_n^{1}u^{(n-1)}v^{(1)} + ....+ C_n^{n}uv^{(n)} = \sum^{n}_{k=0}C^k_nu^{(k)}v^{(n-k)} (uv)(n)=Cn0u(n)v+Cn1u(n−1)v(1)+....+Cnnuv(n)=k=0∑nCnku(k)v(n−k) 泰勒级数 f ( x ) = ∑ n = 0 ∞ f ( n ) x 0 n ! ( x − x 0 ) n f(x) = \sum^{\infty}_{n=0} \frac{f^{(n)}x_0}{n!}(x-x_0)^n f(x)=∑n=0∞n!f(n)x0(x−x0)n 则n阶导数的次数是$a_n = \frac{f^{(n)}}{n!} $ ,对应x-x0的n次方 偶函数在0点的展开项只有偶次项、同理奇函数只有奇项 【例题】2016数一
归纳法 常见结论 arctan x + arctan 1 / x = π / 2 \arctan x+ \arctan 1/x = \pi/2 arctanx+arctan1/x=π/2 (求导得导数为0,代x=1) 三 隐函数x和y有关系,但是无法使用平时的y=f(x)进行表示,而是使用F(x,y)=0表示。 3.1 定义
x确定了,y也是唯一确定的【函数的本质】 补充: 隐式方程:形同 f(x1,x2,…,xn) = 0 的关系,例如单位元方程x2+y2 -1 = 0 隐函数:由隐式方程所隐含定义的函数。 显函数:形如 y = sin x 【因变量在等号左边,含有自变量的式子在右边】。 隐式方程有时候可变为显函数,但有些隐函数改写成显函数非常困难或不可能 3.2 定理它是一个(数学上的)工具【把隐函数局部显示化】用来回答下面的问题: 以隐函数表示的多变量函数,这函数的变量在局部上是否存在显式的关系?隐函数定理说明,对于一个由关系 f(x, y)=0 表示的隐函数,如果它在某一点的偏微分满足某些条件,则在这点有邻域使得在该邻域内 y 可以表示成关于 x 的函数。
参数方程和隐函数共存时直接用公式求4个参数更快 证明 类似链式法则证明,略 四 基础题型选填:特殊函数法,符合的不一定对但不符合的一定错 lim 存在且分子为0,则分母lim也为0,若该函数连续则可取极限值f(x0)=0 利用导数的等价定义 可用的反例 |X| 4.1 概念
题目说了可导,就是说极限存在了 熟练使用公式转换 u ( x ) v ( x ) = e v ( x ) l n u ( x ) u(x)^{v(x)} = e^{v(x)lnu(x)} u(x)v(x)=ev(x)lnu(x) 显函数求导 根据导数定义拼凑等式
参数方程求导 分段函数求导
思想:凑成导数的定义式子、利用一些结论 注意:题目没说可导,而是要证明可导,不能直接洛必达 (命题点)整体存在局部未必存在。如lim 【fx± gy】 存在,不能得出fx、gy存在,因为不存在±不存在可能是存在。如lim(n±n)=0 抽象函数可导性判别 需保证从多侧均趋于0,如f(1-cosx)只能趋于0+,必错 可导+可导 =可导、可导+不可导=不可导 f(x)可导推不出|f(x)|可导,同理反之也推不出。如x,f(x)=±1,(x>0,x |
【本文地址】
今日新闻 |
推荐新闻 |



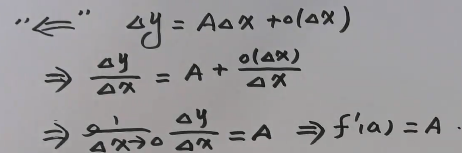

 (
u
v
w
)
′
=
(
u
v
w
)
′
=
u
′
v
w
+
u
(
v
w
)
′
=
u
′
v
w
+
u
[
v
′
w
+
v
w
′
]
=
u
′
v
w
+
u
v
′
w
+
u
v
w
′
\begin{align} (uvw)'& = (u vw)' \\ & = u'vw + u(vw)' \\ & = u'vw + u[v'w + vw'] \\ & = u'vw + uv'w + uvw' \end{align}
(uvw)′=(uvw)′=u′vw+u(vw)′=u′vw+u[v′w+vw′]=u′vw+uv′w+uvw′
(
u
v
w
)
′
=
(
u
v
w
)
′
=
u
′
v
w
+
u
(
v
w
)
′
=
u
′
v
w
+
u
[
v
′
w
+
v
w
′
]
=
u
′
v
w
+
u
v
′
w
+
u
v
w
′
\begin{align} (uvw)'& = (u vw)' \\ & = u'vw + u(vw)' \\ & = u'vw + u[v'w + vw'] \\ & = u'vw + uv'w + uvw' \end{align}
(uvw)′=(uvw)′=u′vw+u(vw)′=u′vw+u[v′w+vw′]=u′vw+uv′w+uvw′