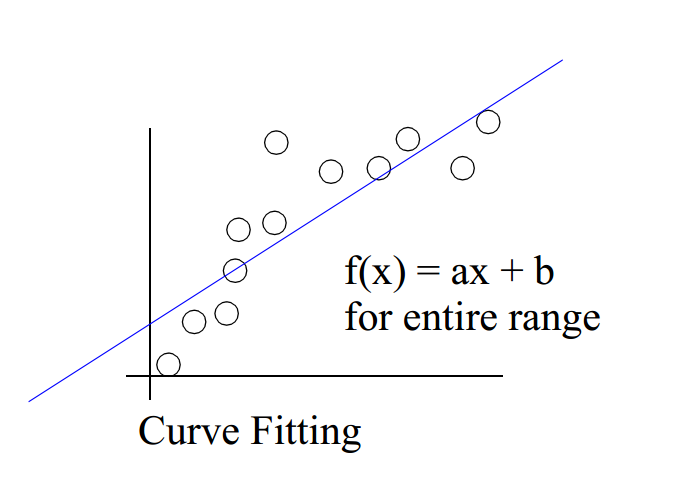
曲线拟合用于查找一系列数据点的“最佳拟合”线或曲线。 大多数情况下，曲线拟合将产生一个函数，可用于在曲线的任何位置找到点。 在某些情况下，也可能不关心找到函数，而是只想使用曲线拟合来平滑数据并改善绘图的外观。

简而言之，曲线拟合就是在受到一定约束条件的情况下，构建可以表示一系列数据点的曲线或数学函数的过程。更加数学化一点的话，对于一个给定的数据集，曲线拟合是以方程形式引入因变量和自变量之间的数学关系的过程。

一般来说，曲线拟合可以认为有以下形式：

平滑

我们使用一个函数来尽可能的表示（即逼近）数据集中点的数据。

逼近

或者如前文所述，我们只想使用曲线拟合来平滑数据并改善绘图的外观。前两种情况下，数据的一般会有相当程度的误差或噪声。

如下所示，为线性拟合：

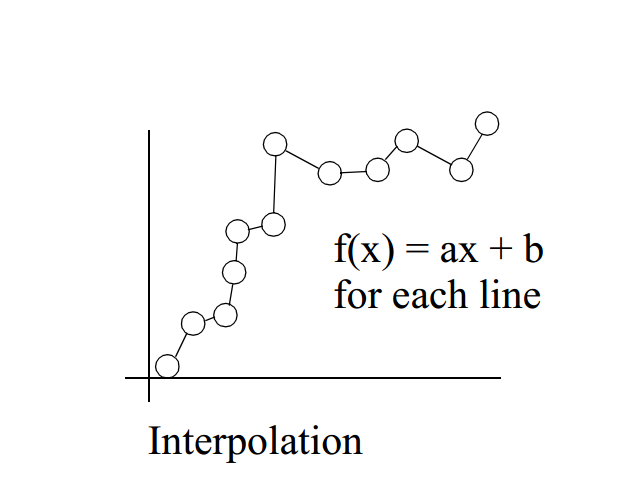
插值

对于给定的数据集，产生一个或多个插值曲线通过数据集的每一个点。这种情况下，我们认为数据点很足够准确的。

如图所示，为线性插值：

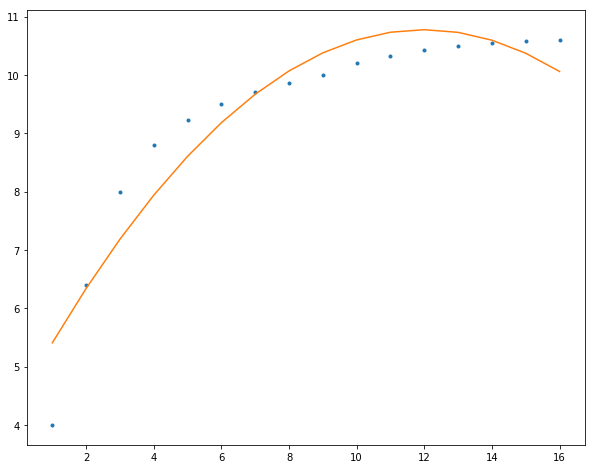
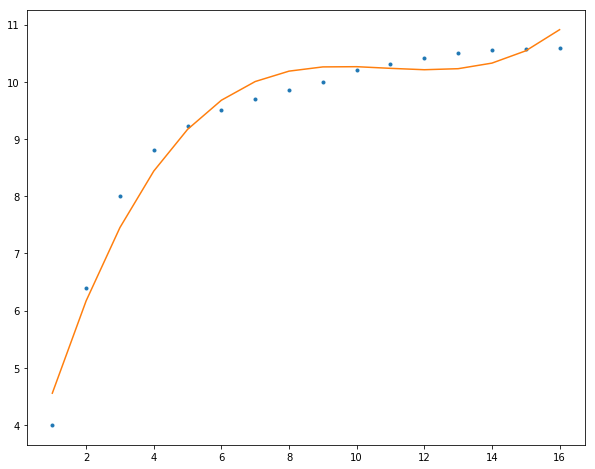
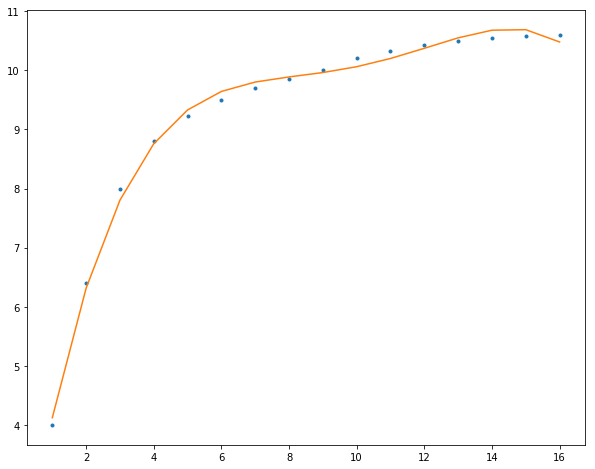
这里我们主要讲述在一定约束条件下，如何用一个函数尽可能的表示（即逼近）数据集中的点。同时，使用基于最小二乘的多项式曲线来拟合数据点。

多项式曲线即为用多项式函数表示的曲线：

f(x)=an∗xn+an−1∗xn−1+⋅⋅⋅+a2∗x2+a1∗x+a0f(x)=a_n*x^n+a_{n-1}*x^{n-1}+···+a_2*x^2+a_1*x+a_0 f(x)=an​∗xn+an−1​∗xn−1+⋅⋅⋅+a2​∗x2+a1​∗x+a0​

f(x)=∑i=0nai∗xif(x)=\sum_{i=0}^{n}{a_i*x^i} f(x)=i=0∑n​ai​∗xi

其中nnn代表多项式函数的阶次（degree）。

当nnn为1时，即为线性函数y=a∗x+by=a*x+by=a∗x+b，nnn为2时，则是二次函数(quadratic function)，nnn为3时，自然是三次函数（cubic function）。

这样对于数据集中的nnn个点(x,y)(x,y)(x,y)，都有：

{y1^(x,w)=w0+w1∗x1+w2∗x12+⋅⋅⋅+wm−1∗x1m−1+wm∗x1my2^(x,w)=w0+w1∗x2+w2∗x22+⋅⋅⋅+wm−1∗x2m−1+wm∗x2m⋮yn−1^(x,w)=w0+w1∗xn−1+w2∗xn−12+⋅⋅⋅+wm−1∗xn−1m−1+wm∗xn−1myn^(x,w)=w0+w1∗xn+w2∗xn2+⋅⋅⋅+wm−1∗xnm−1+wm∗xnm\left\{\begin{matrix} \hat{y_1}(x,w)=w_0+w_1*x_1+w_2*x_1^2+···+w_{m-1}*x_1^{m-1}+w_m*x_1^m \\ \hat{y_2}(x,w)=w_0+w_1*x_2+w_2*x_2^2+···+w_{m-1}*x_2^{m-1}+w_m*x_2^m \\ \vdots \\ \hat{y_{n-1}}(x,w)=w_0+w_1*x_{n-1}+w_2*x_{n-1}^2+···+w_{m-1}*x_{n-1}^{m-1}+w_m*x_{n-1}^m \\ \hat{y_n}(x,w)=w_0+w_1*x_n+w_2*x_n^2+···+w_{m-1}*x_n^{m-1}+w_m*x_n^m \end{matrix}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​y1​^​(x,w)=w0​+w1​∗x1​+w2​∗x12​+⋅⋅⋅+wm−1​∗x1m−1​+wm​∗x1m​y2​^​(x,w)=w0​+w1​∗x2​+w2​∗x22​+⋅⋅⋅+wm−1​∗x2m−1​+wm​∗x2m​⋮yn−1​^​(x,w)=w0​+w1​∗xn−1​+w2​∗xn−12​+⋅⋅⋅+wm−1​∗xn−1m−1​+wm​∗xn−1m​yn​^​(x,w)=w0​+w1​∗xn​+w2​∗xn2​+⋅⋅⋅+wm−1​∗xnm−1​+wm​∗xnm​​

将其写为矩阵形式：

Y^=XW\hat{Y}=XW Y^=XW

其中，W= （w_0,w_1,w_2,···,w_{m-1},w_m)^T，为(m+1)×1(m+1)\times 1(m+1)×1的矩阵，XXX为n×(m+1)n\times (m+1)n×(m+1)的矩阵

X=[111⋯1x1x2x3⋯xn⋮⋮⋮⋮⋮x1mx2mx3m⋯xnm]TX=\begin{bmatrix} 1 & 1 & 1 & \cdots & 1\\ x_1 & x_2 & x_3 & \cdots & x_n \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ x_1^m & x_2^m & x_3^m & \cdots & x_n^m \end{bmatrix}^T X=⎣⎢⎢⎡​1x1​⋮x1m​​1x2​⋮x2m​​1x3​⋮x3m​​⋯⋯⋮⋯​1xn​⋮xnm​​⎦⎥⎥⎤​T

自然，我们可以看到随着mmm也就是degreedegreedegree的增大，多项式曲线可以拟合的数据就可以更加复杂。

实际上，我们可以发现多项式曲线拟合所使用的多项式模型，是一个针对非线性函数数据的线性模型。

这样，多项式曲线拟合即可表示为，给定数据集，求近似曲线f(x)f(x)f(x)，使得近似曲线和yyy的误差最小。

有了模型，这下我们使用最小二乘法来求解WWW。

对于矩阵方程：Ax=bAx=bAx=b, 根据b∈Rm×1b\in R^{m\times 1}b∈Rm×1, A∈Rm×nA\in R^{m\times n}A∈Rm×n的不同，有以下三种形式：

假定bbb存在加性观测误差或噪声，即b=b0+eb=b_0+eb=b0​+e，其中b0b_0b0​为无误差数据向量，eee为误差向量。

为了抵消误差对矩阵方程的求解的影响，我们引入一校正向量Δb\Delta bΔb，使得b+Δb=b0+e+Δb→b0b+\Delta b=b_0+e+\Delta b\rightarrow b_0b+Δb=b0​+e+Δb→b0​，从而实现

Ax=b+Δb⇒Ax=b0Ax=b+\Delta b\Rightarrow Ax=b_0 Ax=b+Δb⇒Ax=b0​

的转换。也就是说，选择校正向量Δb=Ax−b\Delta b=Ax-bΔb=Ax−b，并使校正向量“尽可能小”，则可以实现无误差的矩阵方程Ax=b0Ax=b_0Ax=b0​的求解。

矩阵方程的这一求解思想可以用下面的优化问题描述

minx∣∣Δb∣∣2=∣∣Ax−b∣∣22=(Ax−b)T(Ax−b)\mathop{min}_x ||\Delta b||^2=||Ax-b||^2_2=(Ax-b)^T(Ax-b) minx​∣∣Δb∣∣2=∣∣Ax−b∣∣22​=(Ax−b)T(Ax−b)

这一方法被称为普通最小二乘（Ordinary least squares, OLS）法，一般称为最小二乘法。

于是，矩阵方程的Ax=bAx=bAx=b的最小二乘解为

x^LS=argminx∣∣Ax−b∣∣22\hat{x}_{LS}=arg\mathop{min}_x||Ax-b||^2_2 x^LS​=argminx​∣∣Ax−b∣∣22​

展开ϕ=(Ax−b)T(Ax−b)\phi =(Ax-b)^T(Ax-b)ϕ=(Ax−b)T(Ax−b)得

ϕ=xTATAx−xTATb−bTAx+bTb\phi = x^TA^TAx-x^TA^Tb-b^TAx+b^Tb ϕ=xTATAx−xTATb−bTAx+bTb

求ϕ\phiϕ相对于xxx的导数，并令结果等于零，则有

dϕdx=2ATAx−2ATb=0\frac{d\phi}{dx}=2A^TAx-2A^Tb=0 dxdϕ​=2ATAx−2ATb=0

也就是说，xxx必然满足

ATAx=ATbA^TAx=A^Tb ATAx=ATb

当矩阵Am×nA_{m\times n}Am×n​具有不同的秩时，上述方程的解不同：

超定方程(m>nm>nm>n)列满秩时，即rank(A)=nrank(A)=nrank(A)=n

由于ATAA^TAATA非奇异，所以方程有唯一解

xLS=(ATA)−1ATbx_{LS}=(A^TA)^{-1}A^Tb xLS​=(ATA)−1ATb

对于不满秩（rank(A) print(np.polyfit(x, y, 3))>>> [ 0.00624491 -0.20371114 2.18193147 2.57208791]

最后，我们使用多项式曲线拟合我们的数据，阶数越高，模型参数更多就可以表示更加复杂的数据：

2阶

3阶

4阶

作者: Sikasjc

链接: http://sikasjc.github.io/2018/10/24/curvefitting/

知识共享署名-非商业性使用 4.0 国际许可协议