图论 |
您所在的位置:网站首页 › 多起点最短路径 › 图论 |
图论
|
图论-多源最短路路径算法:弗洛伊德算法
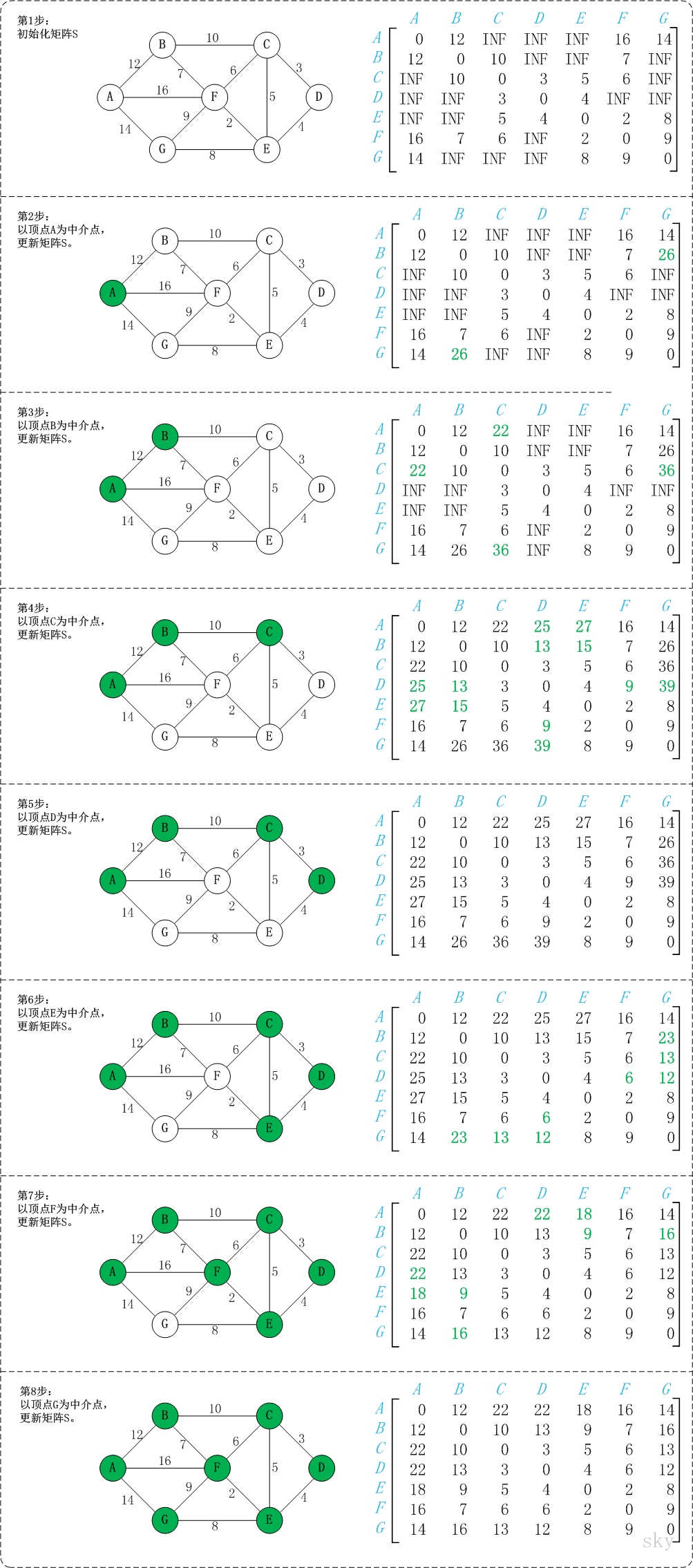
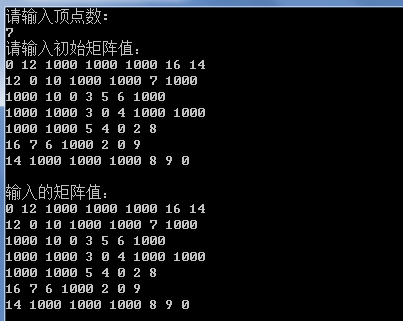
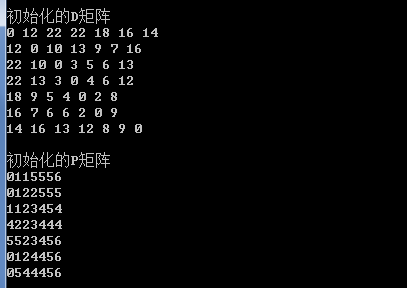
多源最短路指的是执行一次该算法之后,我们能得到任意点之间的最短路径,而不是像dijkstra算法那样只能得到两个点之间的。虽然我们可以直接对每个顶点通过迪杰斯特拉算法求得所有的顶点到所有顶点的时间复杂度,时间复杂度为O(n*3),但是弗洛伊德算法更加简洁优雅 因为使用了三重循环,所以时间复杂度是O(n^3)的 Floyd算法适用于APSP(All Pairs Shortest Paths,多源最短路径),是一种动态规划算法,稠密图效果最佳,边权可正可负。 此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法,也要高于执行|V|次SPFA算法。 优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。 缺点:时间复杂度比较高O(n*3),不适合计算大量数据。补充: 求最短路径的几种情况和对应的算法 有向无环图(DAG, Directed Acyclic Graph):拓扑排序,O(n)的 有向有环图和无向图:迪杰斯特拉算法(单源,O(n^2)的)、弗洛伊德算法(多源,O(n^3)的) 弗洛伊德基本思想弗洛伊德算法作为求最短路径的经典算法,其算法实现相比迪杰斯特拉等算法是非常优雅的,可读性和理解都非常好。 基本思想: 弗洛伊德算法定义了两个二维矩阵: 矩阵 D 记录顶点间的最小路径 例如 D[0][3]= 10,说明顶点 0 到 3 的最短路径为 10; 矩阵 P 记录顶点间最小路径中的中转点 例如 P[0][3]= 1 说明,0 到 3 的最短路径轨迹为:0 -> 1 -> 3。它通过 3 重循环,k 为中转点,v 为起点,w 为终点,循环比较 D[v][w] 和 D[v][k] + D[k][w] 最小值,如果 D[v][k] + D[k][w] 为更小值,则把 D[v][k] + D[k][w] 覆盖保存在 D[v][w] 中。 概念是比较难理解的,我们来看图: 顶点名称和下标的对应 A B C D E F G 0 1 2 3 4 5 6 第 2 步: 以 A 为中间点,原 D 矩阵中,D[B][G] 的值为 INF,即不存在 B->G 的最小路径,但是通过 A 为中间点,D[B][A] + D[A][G] = 12 + 14 = 26 小于 D[B][G] = INF, 所以 D[B][A] + D[A][G] 为 B -> G 的最小值,因此覆盖 D[B][G] 为 26。 第 3 步: 以 B 为中间点,第 2 步后的 D 矩阵中,D[A][C] 的值为 INF, 但是通过 B,D[A][B] + D[B][C] = 12 + 10 = 22 小于 D[A][C] = INF,所以 D[A][B] + D[B][C] 为 A->C 的最小路径,覆盖 D[A][C] 的值为 22, 以此类推。 第 4 步…. 代码实现我们就对上面的图进行弗洛伊德算法求最短路径,并且我们求 A 到 D 的最小路径,即 v = 0, w = 3; 结构定义 typedef struct struct_graph{ char vexs[MAXN]; int vexnum;//顶点数 int edgnum;//边数 int matirx[MAXN][MAXN];//邻接矩阵 } Graph; 弗洛伊德算法 //这里是弗洛伊德算法的核心部分 //k为中间点 for(k = 0; k < G.vexnum; k++){ //v为起点 for(v = 0 ; v < G.vexnum; v++){ //w为终点 for(w =0; w < G.vexnum; w++){ if(D[v][w] > (D[v][k] + D[k][w])){ D[v][w] = D[v][k] + D[k][w];//更新最小路径 P[v][w] = P[v][k];//更新最小路径中间顶点 } } } } 求 A 到 D 的最短路径 v = 0; w = 3; //求 0 到 3的最小路径 printf("\n%d -> %d 的最小路径为:%d\n", v, w, D[v][w]); k = P[v][w]; printf("path: %d", v);//打印起点 while(k != w){ printf("-> %d", k);//打印中间点 k = P[k][w]; } printf("-> %d\n", w); 完整代码 #include #include #define MAXN 10 #define INF = 1000 typedef struct struct_graph{ char vexs[MAXN]; int vexnum;//顶点数 int edgnum;//边数 int matirx[MAXN][MAXN];//邻接矩阵 } Graph; int pathmatirx[MAXN][MAXN];//记录对应点的最小路径的前驱点,例如p(1,3) = 2 说明顶点1到顶点3的最小路径要经过2 int shortPath[MAXN][MAXN];//记录顶点间的最小路径值 void short_path_floyd(Graph G, int P[MAXN][MAXN], int D[MAXN][MAXN]){ int v, w, k; //初始化floyd算法的两个矩阵 for(v = 0; v < G.vexnum; v++){ for(w = 0; w < G.vexnum; w++){ D[v][w] = G.matirx[v][w]; P[v][w] = w; } } //这里是弗洛伊德算法的核心部分 //k为中间点 for(k = 0; k < G.vexnum; k++){ //v为起点 for(v = 0 ; v < G.vexnum; v++){ //w为终点 for(w =0; w < G.vexnum; w++){ if(D[v][w] > (D[v][k] + D[k][w])){ D[v][w] = D[v][k] + D[k][w];//更新最小路径 P[v][w] = P[v][k];//更新最小路径中间顶点 } } } } printf("\n初始化的D矩阵\n"); for(v = 0; v < G.vexnum; v++){ for(w = 0; w < G.vexnum; w++){ printf("%d ", D[v][w]); } printf("\n"); } printf("\n初始化的P矩阵\n"); for(v = 0; v < G.vexnum; v++){ for(w = 0; w < G.vexnum; w++){ printf("%d", P[v][w]); } printf("\n"); } v = 0; w = 3; //求 0 到 3的最小路径 printf("\n%d -> %d 的最小路径为:%d\n", v, w, D[v][w]); k = P[v][w]; printf("path: %d", v);//打印起点 while(k != w){ printf("-> %d", k);//打印中间点 k = P[k][w]; } printf("-> %d\n", w); } int main(){ int v, w; Graph G; printf("请输入顶点数:\n"); scanf("%d", &G.vexnum); printf("请输入初始矩阵值:\n"); for(v = 0; v < G.vexnum; v++){ for(w = 0; w < G.vexnum; w++){ scanf("%d", &G.matirx[v][w]); } } printf("\n输入的矩阵值:\n"); for(v = 0; v < G.vexnum; v++){ for(w = 0; w < G.vexnum; w++){ printf("%d ", G.matirx[v][w]); } printf("\n"); } short_path_floyd(G, pathmatirx, shortPath); } 操作结果 初始化操作下面是Java版本的算法: package com.jiading; import java.util.Scanner; public class Floyd { public static int MaxValue = 100000; public static int[][] path; public static void main(String[] args) { Scanner input = new Scanner(System.in); System.out.println("请输入顶点数和边数:"); //顶点数 int vertex = input.nextInt(); //边数 int edge = input.nextInt(); int[][] matrix = new int[vertex][vertex]; //初始化邻接矩阵 for (int i = 0; i < vertex; i++) { for (int j = 0; j < vertex; j++) { matrix[i][j] = MaxValue; } } //初始化路径数组 path = new int[matrix.length][matrix.length]; //初始化边权值 for (int i = 0; i < edge; i++) { System.out.println("请输入第" + (i + 1) + "条边与其权值:"); int source = input.nextInt(); int target = input.nextInt(); int weight = input.nextInt(); matrix[source][target] = weight; /* 加上下面这一句就表示无向图,否则就是有向图 */ matrix[target][source]=weight; } //调用算法计算最短路径 floyd(matrix); } //非递归实现 public static void floyd(int[][] matrix) { for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix.length; j++) { /** * path的初始化是-1 */ path[i][j] = -1; } } for (int m = 0; m < matrix.length; m++) { for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix.length; j++) { if (matrix[i][m] + matrix[m][j] < matrix[i][j]) { matrix[i][j] = matrix[i][m] + matrix[m][j]; //记录经由哪个点到达 path[i][j] = m; } } } } for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix.length; j++) { if (i != j) { if (matrix[i][j] == MaxValue) { System.out.println(i + "到" + j + "不可达"); } else { System.out.print(i + "到" + j + "的最短路径长度是:" + matrix[i][j]); System.out.print("最短路径为:" + i + "->"); findPath(i, j); System.out.println(j); } } } } } //递归寻找路径 public static void findPath(int i, int j) { int m = path[i][j]; if (m == -1) { return; } /* path[i][j]中保存的点是一定会经过的,但是不一定是第一个经过的,所以从i到m之间也需要再求中间点,直到没有中间点 */ findPath(i, m); System.out.print(m + "->"); findPath(m, j); } } |
【本文地址】
今日新闻 |
推荐新闻 |