【统计学笔记】第十二章 多元线性回归 |
您所在的位置：网站首页 › 多元线性回归的检验方法是 › 【统计学笔记】第十二章 多元线性回归 |
【统计学笔记】第十二章 多元线性回归
|
方差分析表和回归分析表的解读 各种统计量检验的决策准则 各种假设检验的假设的建立 第十二章 多元线性回归 12.1 多元线性回归模型 多元回归：一个因变量与两个及两个以上自变量的回归 12.1.1 多元回归模型与回归方程 多元回归模型：描述因变量 y 如何依赖于自变量 x 1 ， x 2 ， … ， x k x_1 ， x_2 ，…， x_k x1，x2，…，xk 和误差项 ε ε ε 的方程，其一般形式可表示为： y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β k x k + ε （ 其 中 β 0 + β 1 β 2 + . . . + β k 是 模 型 的 参 数 ； ε 为 误 差 项 ） y = β_0 + β_1x_1 + β_2x_2 + ... + β_kx_k + ε \\ （其中 β_0+β_1β_2+...+β_k 是模型的参数；ε为误差项） y=β0+β1x1+β2x2+...+βkxk+ε（其中β0+β1β2+...+βk是模型的参数；ε为误差项） 误差项 ε ε ε 有三个基本假定 正态性：误差项 ε ε ε 是一个服从正态分布的随机变量，且期望值为0，即 ε ∼ N ( 0 , σ 2 ) ε \sim N(0,\sigma^2) ε∼N(0,σ2)方差齐性：对于自变量 x 1 , x 2 , … , x k x_1,x_2,…,x_k x1,x2,…,xk 的所有值， ε ε ε 的方差 σ 2 \sigma^2 σ2 都相同独立性：对于自变量 x 1 , x 2 , … , x k x_1, x_2,…,x_k x1,x2,…,xk 的一组特定值，它所对应的 ε ε ε 与任意一组其他值所对应的不相关 多元回归方程：描述因变量y的期望 E ( y ) E(y) E(y) 与自变量 x 1 , x 2 , … , x k x_1,x_2,…,x_k x1,x2,…,xk 关系的方程，根据回归模型的假定有： E ( y ) = β 0 + β 1 x 1 + β 2 x 2 + . . . + β k x k E(y) = β_0 + β_1x_1 + β_2x_2 + ... + β_kx_k E(y)=β0+β1x1+β2x2+...+βkxk 特殊的对于有两个自变量的多元回归方程，其形式为： E ( y ) = β 0 + β 1 x 1 + β 2 x 2 E(y) = β_0 + β_1x_1 + β_2x_2 E(y)=β0+β1x1+β2x2
12.1.2 估计的多元回归方程
估计的多元回归方程：用样本统计量
β
^
1
,
β
^
2
,
.
.
.
.
,
β
^
k
\hatβ_1,\hatβ_2,....,\hat β_k
β^1,β^2,....,β^k 估计回归方程中的参数
β
0
+
β
1
x
1
+
β
2
x
2
+
.
.
.
+
β
k
x
k
β_0 + β_1x_1 + β_2x_2 + ... + β_kx_k
β0+β1x1+β2x2+...+βkxk 时得到的方程
y
=
β
^
0
+
β
^
1
x
1
+
β
^
2
x
2
+
.
.
.
+
β
^
k
x
k
（
其
中
β
^
1
,
β
^
2
,
.
.
.
.
,
β
^
k
称
为
偏
回
归
系
数
；
β
^
i
表
示
当
x
1
.
.
.
x
i
−
1
和
x
i
+
1
.
.
.
x
k
不
变
时
，
x
i
每
变
动
一
个
单
位
因
变
量
y
的
平
均
变
动
量
）
y = \hatβ_0 + \hatβ_1x_1 + \hatβ_2x_2 + ... + \hatβ_kx_k\\ （其中 \hatβ_1,\hatβ_2,....,\hat β_k称为偏回归系数；\\ \hat β_i表示当x_1...x_{i-1}和x_{i+1}...x_k不变时，x_i每变动一个单位因变量y的平均变动量）
y=β^0+β^1x1+β^2x2+...+β^kxk（其中β^1,β^2,....,β^k称为偏回归系数；β^i表示当x1...xi−1和xi+1...xk不变时，xi每变动一个单位因变量y的平均变动量）
12.1.3 参数的最小二乘估计
这都要计算机算了考试谁会出这个来计算啊，所以pass S S T （ 总 平 方 和 ） = S S E （ 残 差 平 方 和 ） + S S R （ 回 归 平 方 和 ） SST（总平方和） = SSE（残差平方和） + SSR（回归平方和） SST（总平方和）=SSE（残差平方和）+SSR（回归平方和） 多重判定系数：是回归平方和占总平方和的比例，是度量多元回归方程拟合程度的一个统计量，反映了因变量y取值的变差中，能被估计的多元回归方程所解释的比例。 R 2 = S S R S S T = 1 − S S E S S T R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST} R2=SSTSSR=1−SSTSSE调整的多重判定系数：为避免增加自变量而高估 R 2 R^2 R2，用样本量n和自变量的个数 k k k 去修正 R 2 R^2 R2 得到，其数值永远小于 R 2 R^2 R2 ，意义和 R 2 R^2 R2 类似 R a 2 = 1 − ( 1 − R 2 ) ( n − 1 n − k − 1 ) R_a^2 = 1 - (1 - R^2)(\frac{n-1}{n-k-1}) Ra2=1−(1−R2)(n−k−1n−1) 12.2.2 估计标准误差 估计标准误差（ s e s_e se）：是误差项 ε ε ε的方差 σ \sigma σ的一个估计值，它在衡量多元回归方程的拟合优度方面起着重要作用：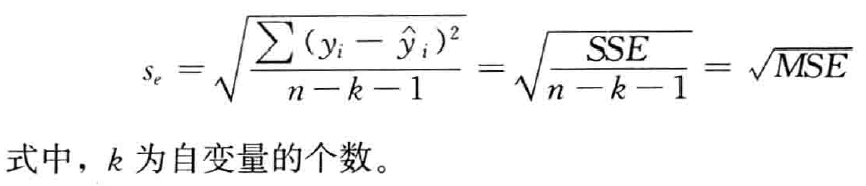
12.3 显著性检验
12.3.1 线性关系检验
线性关系检验是检验因变量y与所有k个自变量之间的线性关系是否显著,也被称为总体的显著性检验。 1）提出假设： H 0 : β 1 = β 2 = . . . = β k = 0 ； H 1 : β 1 , β 2 , . . . , β k 至 少 有 一 个 不 等 于 0 ； H_0:β_1 = β_2 = ... = β_k = 0 ；\\ \qquad\qquad H_1:β_1,β_2 ,...,β_k \;至少有一个不等于0； H0:β1=β2=...=βk=0；H1:β1,β2,...,βk至少有一个不等于0；2）计算检验的统计量 F F F： F = S S R / k S S E / ( n − k − 1 ) = M S R M S E = ∼ F ( k , n − k − 1 ) F = \frac{SSR/k}{SSE/(n-k-1)} = \frac{MSR}{MSE} = \sim F(k,n-k-1) F=SSE/(n−k−1)SSR/k=MSEMSR=∼F(k,n−k−1)3）做出统计决策： 给定显著性水平 α \alpha α在 F F F分布表中寻找 F α ( k , n − k − 1 ) F_\alpha(k,n-k-1) Fα(k,n−k−1)比较 F F F和 F α F_\alpha Fα （或者比较 P P P值和 α \alpha α） F > F α （ 或 P < α ） F > F_\alpha（或PFα（或P α ） F < F_\alpha（或P>\alpha） Fα）：不拒绝原假设 H 0 H_0 H0 12.3.2 回归系数检验与推断 1）提出假设： 对 任 意 参 数 β i ( i = 1 , 2 , . . . , k ) ： H 0 : β i = 0 ； H 1 : β i ≠ 0 ； 对任意参数\beta_i(i = 1,2,...,k)：\\ H_0:β_i = 0 ；\\ H_1:β_i \ne 0； 对任意参数βi(i=1,2,...,k)：H0:βi=0；H1:βi=0；2）计算检验的统计量 t t t： 3）做出统计决策：
给定显著性水平
α
\alpha
α在
t
t
t分布表中寻找
t
α
/
2
(
n
−
k
−
1
)
t_{\alpha/2}(n-k-1)
tα/2(n−k−1)比较
t
t
t和
t
α
t_\alpha
tα （或者比较
P
P
P值和
α
\alpha
α）
∣
t
∣
>
t
α
/
2
|t| > t_{\alpha/2}
∣t∣>tα/2：拒绝原假设
H
0
H_0
H0
∣
t
∣
<
t
α
/
2
|t| < t_{\alpha/2}
∣t∣ |
【本文地址】
今日新闻 |
推荐新闻 |