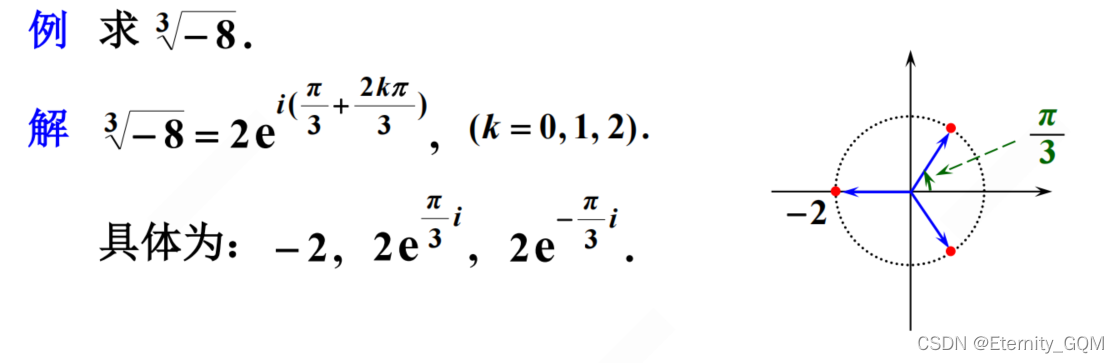【复变函数与积分变换】【第一章 复数与复变函数】 |
您所在的位置:网站首页 › 复数里的模 › 【复变函数与积分变换】【第一章 复数与复变函数】 |
【复变函数与积分变换】【第一章 复数与复变函数】
|
2021-1-3
文章目录
2021-1-3第一章 复数与复变函数§1.1 复数一、复数及其运算定义:复数的基本概念相等
四则运算
二、共轭复数定义性质
§1.2 复数的几种表示复平面一、复数的模与辐角主辐角相互转换关系三减二加,一四不变
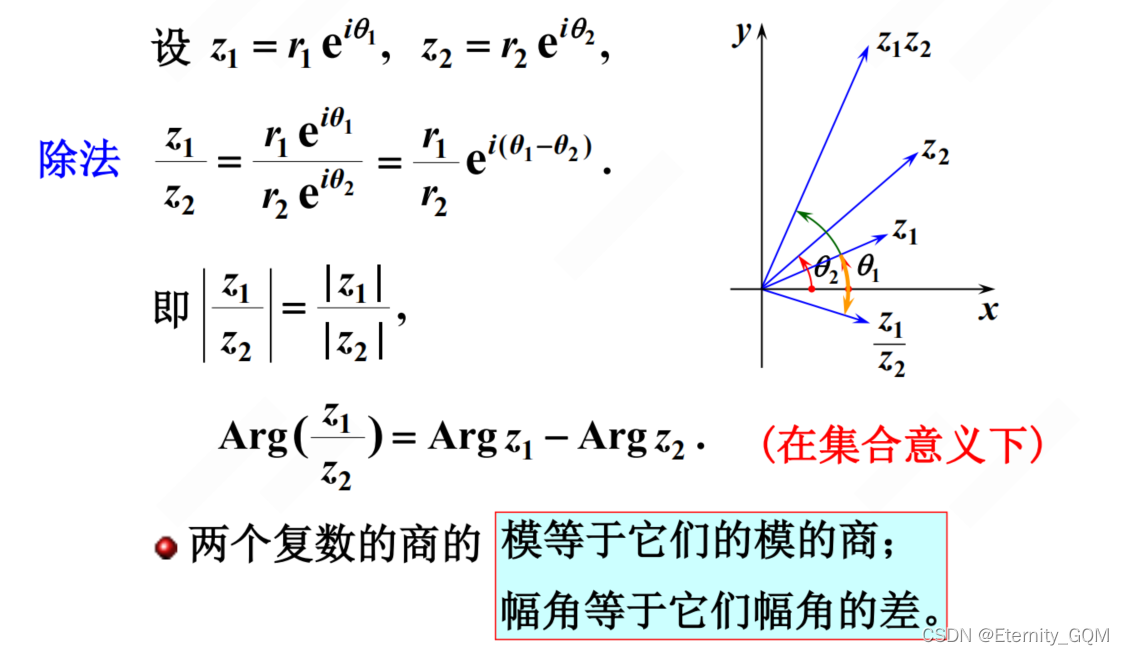
二、复数的三角表示和指数表示三角表示式指数表示式利用指数表示进行复数的乘除法运算简单复数的指数表示形式
三、复数的乘幂与方根复数的乘幂棣莫弗(De Moivre)公式
复数的方根定义:利用复数的指数表示式可以很快得到**开方法则**:方根公式
几个关系
知识拓展——欧拉公式
§1.3 平面点集的一般概念§1.4 无穷大与复球面§1.5 复变函数
❤ 持续更新 ❤!!!!
第一章 复数与复变函数
代数基本定理: 任何多项式在复数域里必有根,而且 n 次多项式恰好有 n 个根 §1.1 复数 一、复数及其运算 定义:(1) 设 x 和 y 是任意两个实数, z = x + i y z=x+iy z=x+iy ( 或者 z = x + y i z=x+yi z=x+yi ) 的数称为复数。其中 i i i 称为虚数单位,即 i = − 1 i = \sqrt{-1} i=−1 (2) x 和 y 分别称为复数 z 的实部与虚部,并分别表示为: x = R e ( z ) x = Re(z) x=Re(z) , y = I m ( z ) y = Im(z) y=Im(z) (3) 当 x = 0 时,z = 0 + iy = iy 称为纯虚数 当 y = 0 时,z = x + i0 = x 就是实数。因此,实数可以看作是复数的特殊情形。 复数的基本概念 相等设 z 1 = x 1 + i y 1 z_1 = x_1 + i y_1 z1=x1+iy1 与 z 2 = x 2 + i y 2 z_2 = x_2 + i y_2 z2=x2+iy2 是两个复数 如果 x 1 = x 2 x_1 = x_2 x1=x2 与 y 1 = y 2 y_1 = y_2 y1=y2 相等, 则称 z 1 z_1 z1与 z 2 z_2 z2 相等 它们之间只有相等与不相等的关系。 特别地, z = x + i y = 0 z = x + i y = 0 z=x+iy=0 当且仅当 x = y = 0 x = y = 0 x=y=0. 注:复数与实数不同,两个复数(虚部不为零)不能比较大小,它们之间只有相等与不相等的关系。 四则运算加法: z 1 + z 2 = x 1 + x 2 + i ( y 1 + y 2 ) z_1 + z_2 = x_1 + x_2 + i( y_1 + y_2 ) z1+z2=x1+x2+i(y1+y2); 减法: z 1 − z 2 = x 1 − x 2 + i ( y 1 − y 2 ) z_1 − z_2 = x_1 − x_2 + i( y_1 − y_2 ) z1−z2=x1−x2+i(y1−y2); 乘法: z 1 ⋅ z 2 = ( x 1 x 2 − y 1 y 2 ) + i ( x 1 y 2 + x 2 y 1 ) z_1· z_2 = (x_1 x_2 − y_1 y_2 ) + i(x_1 y_2 + x_2 y_1 ) z1⋅z2=(x1x2−y1y2)+i(x1y2+x2y1); 除法 :如果存在复数 z z z,使得 z 1 = z 2 ⋅ z z_1 = z_2 ·z z1=z2⋅z,则 z = z 1 z 2 z=\frac{z_1}{z_2} z=z2z1。 加法、乘法满足交换律与结合律,乘法对加法满足分配律.由此可知,在实数域里由这些规律推得的恒等式在复数里仍然有效.另外,还可以验证:复数集关于四则运算是封闭的,其代数结构是域。 交换律、结合律、分配率 二、共轭复数 定义设 z = x + i y z = x + i y z=x+iy 是一个复数, 称 z = x − i y z = x - i y z=x−iy 为 z z z 的共轭复数,记作 z ‾ \overline{z} z。 称
x
2
+
y
2
\sqrt{x^2+y^2}
x2+y2
(算术根)为复数
z
z
z 的模,记作
∣
z
∣
|z|
∣z∣ =
x
2
+
y
2
\sqrt{x^2+y^2}
x2+y2
.
用建立了笛卡儿直角坐标系的平面来表示复数的平面称为复平面.复平面赋予了复数以直观的几何意义,复数的数对表示式也可以看作是直角坐标系中的坐标.它建立了“数”与“点”之间的一一对应关系.此时,x 轴称为实轴,y 轴称为虚轴 把复数
1
+
2
i
1+ 2i
1+2i 称为点
1
+
2
i
1+ 2i
1+2i ,把点
4
+
i
4+ i
4+i 称为复数
4
+
i
4+ i
4+i . 称 x 2 + y 2 \sqrt{x^2+y^2} x2+y2 (算术根)为复数 z z z 的模,记作 ∣ z ∣ |z| ∣z∣ = x 2 + y 2 \sqrt{x^2+y^2} x2+y2 .
(1) 辐角是多值的,相互之间可相差 2kπ ,其中 k 为整数。 (2) 辐角的符号约定为:逆时针取正号,顺时针取负号。 复数 0 的模为 0,辐角无意义。
复数求方根是复数乘幂的逆运算
【复变函数与积分变换】【平面点集的一般概念】 §1.4 无穷大与复球面【复变函数与积分变换】【平面点集的一般概念】 §1.5 复变函数 ❤ 持续更新 ❤!!!! |
【本文地址】
今日新闻 |
推荐新闻 |
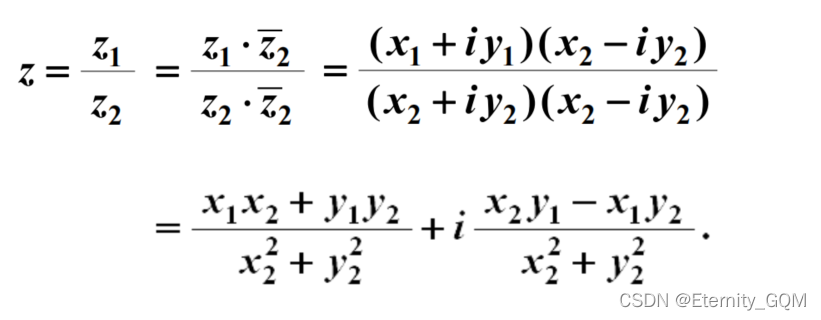
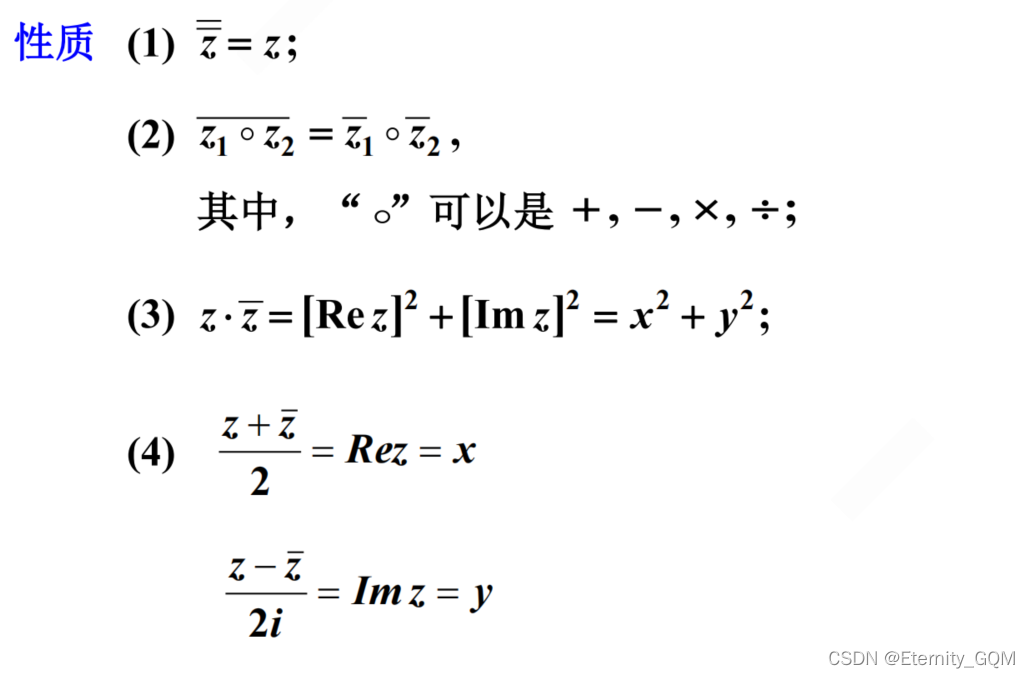
 在复平面上,从原点到点
z
=
x
+
i
y
z = x + i y
z=x+iy 所引的向量与该复数 z 也构成一一对应关系(复数零对应零向量)。
在复平面上,从原点到点
z
=
x
+
i
y
z = x + i y
z=x+iy 所引的向量与该复数 z 也构成一一对应关系(复数零对应零向量)。  引进复平面后,复数 z 与点 z 以及向量 z 视为同一个概念。
引进复平面后,复数 z 与点 z 以及向量 z 视为同一个概念。
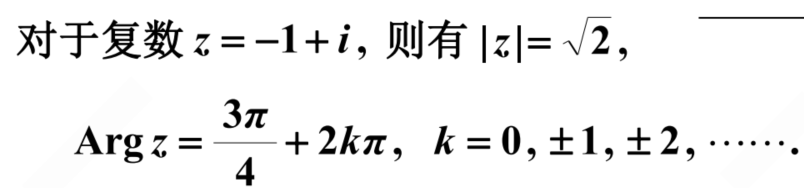
 Arg z = arg z + 2kπ , k = 0, ± 1, ± 2,……
Arg z = arg z + 2kπ , k = 0, ± 1, ± 2,……

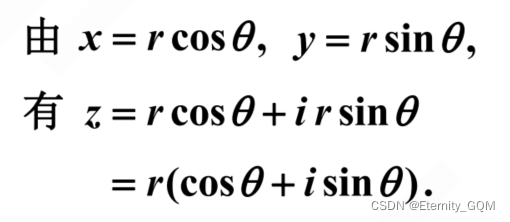




 利用复数的指数表示式可以很快得到乘幂法则:
利用复数的指数表示式可以很快得到乘幂法则: 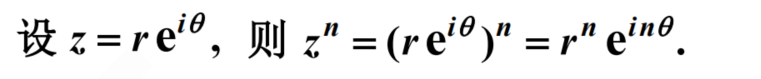

 复数的 n 次方根一般是多值的
复数的 n 次方根一般是多值的
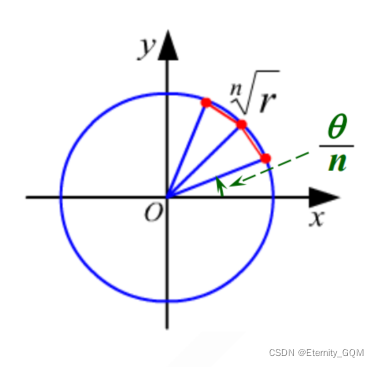
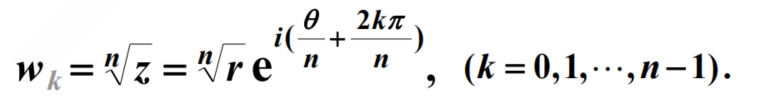 在复平面上, 这 n 个根均匀地分布在一个以原点为中心、以
r
n
\sqrt[n]{r}
nr
为半径的圆周上。其中一个根的辐角是
(
θ
/
n
)
(θ/n)
(θ/n).
在复平面上, 这 n 个根均匀地分布在一个以原点为中心、以
r
n
\sqrt[n]{r}
nr
为半径的圆周上。其中一个根的辐角是
(
θ
/
n
)
(θ/n)
(θ/n).