概率论:假设检验、显著性检验 |
您所在的位置:网站首页 › 备择假设是假设检验的对象吗 › 概率论:假设检验、显著性检验 |
概率论:假设检验、显著性检验
|
一、什么是假设检验?——以双边检验为例
用大白话来讲,假设检验就是检验(判断)某个假设是否正确,并且说出这个判断出错的概率,(判断出错包括了这个假设原本是对的,你判断它是错的;或者这个假设是错的,你判断它是对的)。 这里我引用书本上的一个例子作为说明。 例1 某车间用一台包装机包装葡萄糖.袋装糖的净重是一个随机变量,它服从正态分布.当机器正常时,其均值为0.5kg,标准差为0.015kg.某日开工后为检验包装机是否正常,随机地抽取它所包装的糖9袋,称得净重(kg) 0.497 0.506 0,518 0.524 0.498 0.511 0.520 0.515 0.512 问机器是否正常? 以 μ \mu μ, σ \sigma σ分别表示这一天袋装糖的净重总体X的均值和标准差.由于长期实践表明标准差比较稳定,我们就设 σ \sigma σ=0.015.于是 X N ( μ , 0.01 5 2 ) X~N(\mu,0.015^2) X N(μ,0.0152),这里a未知,问题是根据样本值来判断 μ \mu μ=0.5还是 μ \mu μ≠0.5.为此,我们提出两个相互对立的假设 H 0 : μ = μ 0 = 0.5 H 1 : μ ≠ μ 0 \begin{aligned} &H_{0}: \mu=\mu_{0}=0.5 \\ &H_{1}: \mu \neq \mu_{0} \end{aligned} H0:μ=μ0=0.5H1:μ=μ0 既然假设是说总体均值等于某个值(0.5),一个很自然的想法就是抽一组样本,看样本均值和假设的总体均值相差多少。如果 ∣ x ˉ − μ 0 ∣ |\bar{x}-\mu _0| ∣xˉ−μ0∣相差很多,我们就考虑拒绝这个假设。 现在就面临了两个问题,一个是当两者相差多少时我们拒绝这个假设 H 0 H_0 H0, 当拒绝这个假设时我们所作的判断错误概率是多少(也就是假设为真我们反而拒绝了的概率是多少?,因为在检验时要给出出错的概率,别人才会相信你的检验结果) 之前我们介绍了中心极限定理 中心极限定理是说: 样本的平均值约等于总体的平均值。 不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布。 这里我们可以用上,考虑到 H 0 H_0 H0为真时,由中心极限定理得, X ‾ − μ σ / n = X ‾ − μ 0 σ / n ∼ N ( 0 , 1 ) \frac{\overline{X}-\mu}{\sigma / \sqrt{n}}=\frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}} \sim N(0,1) σ/n X−μ=σ/n X−μ0∼N(0,1)。可以看到这条式子给出了与 ∣ x ˉ − μ 0 ∣ |\bar{x}-\mu _0| ∣xˉ−μ0∣有关的一个概率分布,因此我们可以知道当 ∣ x ˉ − μ 0 ∣ |\bar{x}-\mu _0| ∣xˉ−μ0∣相差为某个数时所作判断出错的概率——我们不妨设 X ‾ − μ σ / n ≥ k \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \geq k σ/n X−μ≥k时拒绝假设 H 0 H_0 H0,也就是 ∣ X ‾ − μ ∣ ≥ k σ / n |\overline{X}-\mu|\geq k\sigma/ \sqrt{n} ∣X−μ∣≥kσ/n 拒绝假设 H 0 H_0 H0, 否则就接受 H 0 H_0 H0。 那么此时实际上 H 0 H_0 H0为真却被拒绝的决策的概率为:
P
{
当
H
0
为
真
拒
绝
H
0
}
=
P
μ
0
{
∣
X
‾
−
μ
0
σ
/
n
∣
⩾
k
}
≤
α
P\{当H_0为真拒绝H_0\}=P_{\mu_{0}}\left\{\left|\frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant k\right\} \leq \alpha
P{当H0为真拒绝H0}=Pμ0{∣∣∣∣σ/n
X−μ0∣∣∣∣⩾k}≤α (同样可以固定出错的概率求相差的数,因为它的概率分布已知),这就能够回答我们上述提出的两个问题了。 并且我们希望这个误判的概率不大于
α
\alpha
α,此时我们就可以确定我们应该设定的k为多大(如下所示)。 统计量 Z = X ˉ − μ 0 σ / n Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} Z=σ/n Xˉ−μ0称为检验统计量。
由于检验法则是根据样本作出的,总有可能作出错误的决策.如上面所说的那样,在假设 H 0 H_0 H0实际上为真时,我们可能犯拒绝 H 0 H_0 H0的错误,称这类“弃真”的错误为第Ⅰ类错误.又当 H 0 H_0 H0实际上不真时,我们也有可能接受 H 0 H_0 H0, 称这类“取伪”的错误为第Ⅱ类错误. 为此,在确定检验法则时,我们应尽可能使犯两类错误的概率都较小.但是,进一步讨论可知,一般来说,当样本容量固定时,若减少犯一类错误的概率,则犯另一类错误的概率往往增大.若要使犯两类错误的概率都减小,除非增加样本容量.在给定样本容量的情况下,一般来说,我们总是控制犯第I类错误的概率,使它不大于 α \alpha α. α \alpha α的大小视具体情况而定,通常 α \alpha α取0.1,0.05,0.01,0.005等值.这种只对犯第I类错误的概率加以控制,而不考虑犯第Ⅱ类错误的概率的检验,称为显著性检验。 三、单边检验设总体 X ∼ N ( μ , σ 2 ) X \sim N\left(\mu, \sigma^{2}\right) X∼N(μ,σ2), μ \mu μ未知, σ \sigma σ已知, X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn是来自X的样本,给定显著性水平 α \alpha α,我们来求检验问题: H 0 : μ ≤ μ 0 , H 1 : μ ≥ μ 0 H_0:\mu \leq \mu _0,H_1: \mu \geq \mu _0 H0:μ≤μ0,H1:μ≥μ0 的拒绝域。 从严格的标准来讲,如果我们取样的样本均值大于 μ 0 \mu _0 μ0,我们就会拒绝 H 0 H_0 H0,但是这是不符合实际情况的,因为样本均值是围绕总体均值波动的,如果一次采样恰好采集到样本值都是比较大的,我们就拒绝这个假设,这是不合适的。 因此,就像前面的双边检验一样,我们允许样本均值 X ‾ \overline X X有在 μ \mu μ周围一定的波动。这里单边检验和双边检验所不同的是,双边检验的 X ‾ \overline X X在概率密度曲线的两边都不能波动得太多,因为双边检验的假设是一个点。相反,单边检测可以在 μ \mu μ左边任意地波动,而在右边不能波动地太多,因为单边检验地假设是小于等于号(如下图所示)。 通过下面的图可以更直观的看到
μ
\mu
μ所允许的波动范围(白色区域)以及拒绝域(黑色区域),其中左侧为双边检验,右侧为单边检验。如果
X
‾
\overline X
X没有经过标准化,那么它服从
N
(
μ
,
σ
)
N(\mu,\sigma)
N(μ,σ);如果经过标准化后变成
X
ˉ
−
μ
σ
/
n
\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}
σ/n
Xˉ−μ,它服从
N
(
0
,
1
)
N(0,1)
N(0,1) 时拒绝假设 H 0 H_0 H0. 但是这里有一个问题,我们并不知道 μ \mu μ的具体值,但是在假设 H 0 H_0 H0成立的情况下,我们有以下推导 X ˉ − μ σ / n ≥ X ˉ − μ 0 σ / n \frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \geq \frac{\bar{X}-\mu _0}{\sigma / \sqrt{n}} σ/n Xˉ−μ≥σ/n Xˉ−μ0 此时如果 X ˉ − μ 0 σ / n ≥ z α \frac{\bar{X}-\mu _0}{\sigma / \sqrt{n}} \geq z_{\alpha} σ/n Xˉ−μ0≥zα,则必有 X ˉ − μ σ / n ≥ z α \frac{\bar{X}-\mu}{\sigma / \sqrt{n}}\geq z_{\alpha} σ/n Xˉ−μ≥zα。因此如果在假设 H 0 H_0 H0成立的情况下,我们仍抽样发现不太支持 H 0 H_0 H0的 X ‾ \overline{X} X出现,我们拒绝 H 0 H_0 H0的理由更充分了(有点类似反证法思维)。当然这里不是完全充分,我们仍有 α \alpha α的概率误判。 至此,我们可以总结道:在误判率不超过 α \alpha α的情况下,单边检测的拒绝域应该为 { X ‾ : X ‾ − μ 0 σ / n ≥ z α } \{\overline X : \frac{\overline{X}-\mu _{0}}{\sigma / \sqrt{n}}\geq z_{\alpha}\} {X:σ/n X−μ0≥zα} 笔者认为这样的讲解思路更容易懂(在不需要应试的情况下完全可以这样理解),但在需要应试的情况下,可以参考下下面的东西:
上面所讨论的正态总体 N ( μ , σ 2 ) N(\mu, \sigma ^2) N(μ,σ2)当标准差 σ \sigma σ已知的情况,使用统计量 Z = X ‾ − μ 0 σ / n Z=\frac{\overline X - \mu _0}{\sigma/\sqrt{n}} Z=σ/n X−μ0来确定拒绝域的检验方法称为Z检验。 2. t检验正态总体 N ( μ , σ 2 ) N(\mu, \sigma ^2) N(μ,σ2)当标准差 σ \sigma σ未知时,使用样本标准差 s s s替代总体标准差 σ \sigma σ并使用统计量 Z = X ‾ − μ 0 s / n Z=\frac{\overline X - \mu _0}{s/\sqrt{n}} Z=s/n X−μ0来确定拒绝域的检验方法称为t检验。 |
【本文地址】
今日新闻 |
推荐新闻 |
 一般来说,我们希望我们对假设做出的判断发生错误的概率越小越好,一般取为0.01,0.05。.数
α
\alpha
α称为显著性水平,上面
x
ˉ
与
μ
0
\bar{x}与\mu _0
xˉ与μ0有无显著差的判断是在显著性水平
α
\alpha
α之下作出的。
一般来说,我们希望我们对假设做出的判断发生错误的概率越小越好,一般取为0.01,0.05。.数
α
\alpha
α称为显著性水平,上面
x
ˉ
与
μ
0
\bar{x}与\mu _0
xˉ与μ0有无显著差的判断是在显著性水平
α
\alpha
α之下作出的。
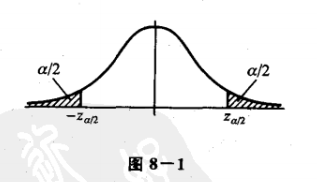
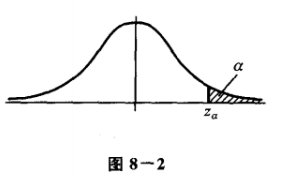 从图中可以很清楚地看到,对于单边检测来说,如果我们希望发生误判的错误率不高于
α
\alpha
α, 那么我们应该在统计检验量z满足:
z
=
X
‾
−
μ
σ
/
n
≥
z
α
z = \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \geq z_{\alpha}
z=σ/n
X−μ≥zα
从图中可以很清楚地看到,对于单边检测来说,如果我们希望发生误判的错误率不高于
α
\alpha
α, 那么我们应该在统计检验量z满足:
z
=
X
‾
−
μ
σ
/
n
≥
z
α
z = \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \geq z_{\alpha}
z=σ/n
X−μ≥zα
