什么是哈密尔顿回路/路径? |
您所在的位置:网站首页 › 基本路径是什么路径啊 › 什么是哈密尔顿回路/路径? |
什么是哈密尔顿回路/路径?
|
一:哈密尔顿回路与哈密尔顿路径
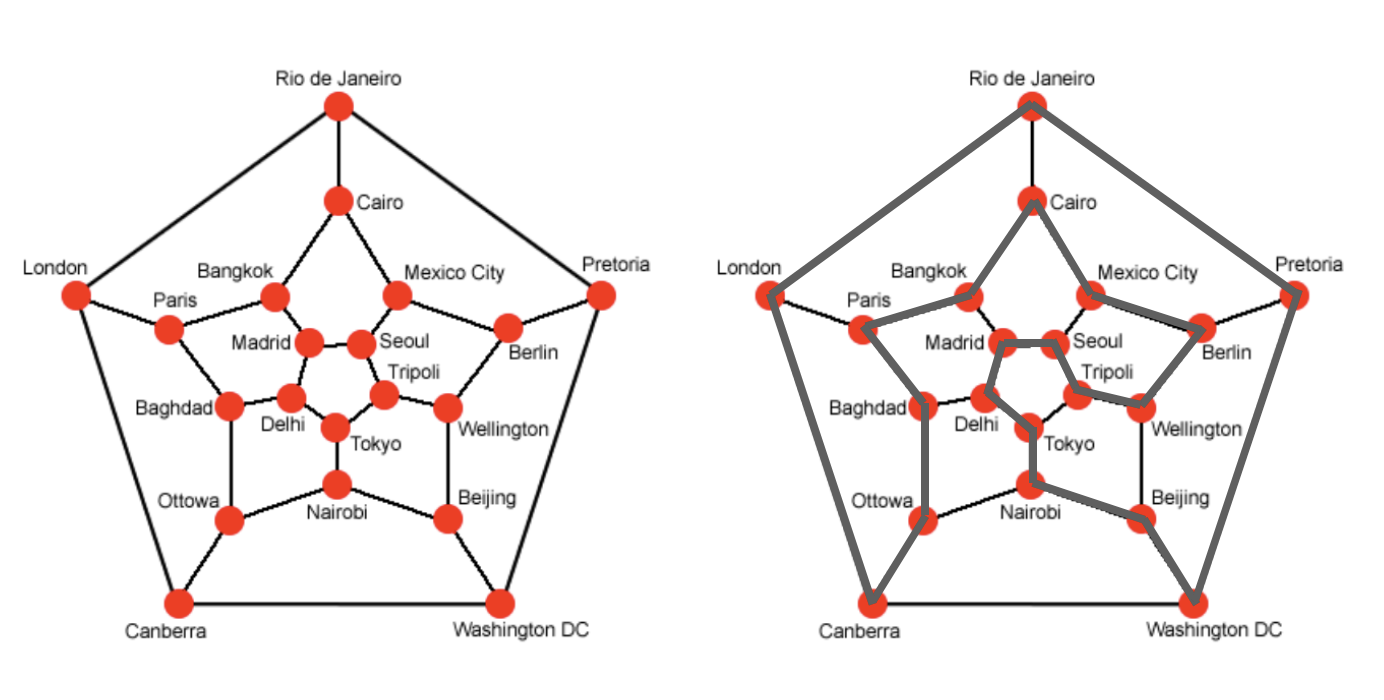
1859 年,爱尔兰数学家哈密尔顿(Hamilton)提出了一个“周游世界”的游戏: 在一个正十二面体的二十个顶点上,标注了伦敦,巴黎,莫斯科等世界著名大城市,正十二面体的棱表示连接着这些城市的路线。要求游戏参与者从某个城市出发,把所有的城市都走过一次,且仅走过一次,然后回到出发点。
简而言之,哈密尔顿回路是指,从图中的一个顶点出发,沿着边行走,经过图的每个顶点,且每个顶点仅访问一次,之后再回到起始点的一条路径。如上图所示,我们的起始点选定为 Washington DC,灰色实线构成的一条路径就是一条哈密尔顿回路。 在图论算法的领域中,哈密尔顿回路(Hamilton Loop)和路径(Hamilton Path)在定义上是有所区分的: 哈密尔顿回路(Hamilton Loop)要求从起始点出发并能回到起始点,其路径是一个环。 哈密尔顿路径(Hamilton Path)并不要求从起始点出发能够回到起始点,也就是说:起始顶点和终止顶点之间不要求有一条边。
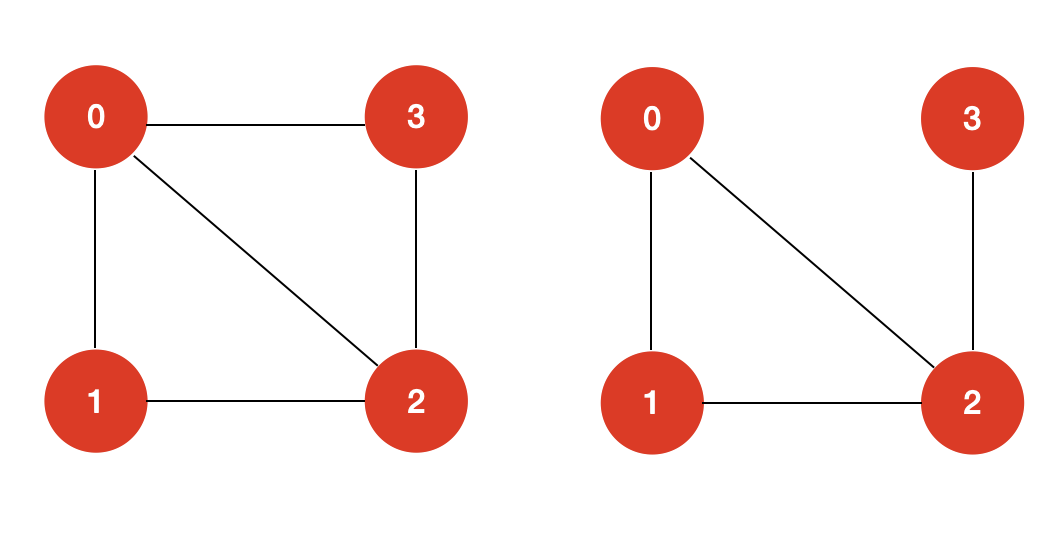
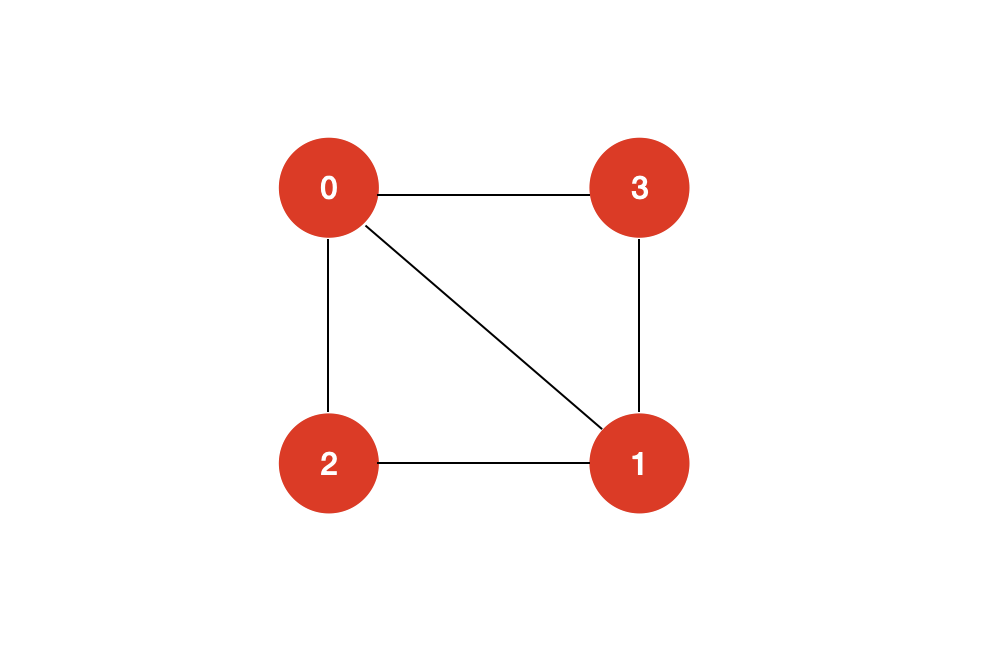
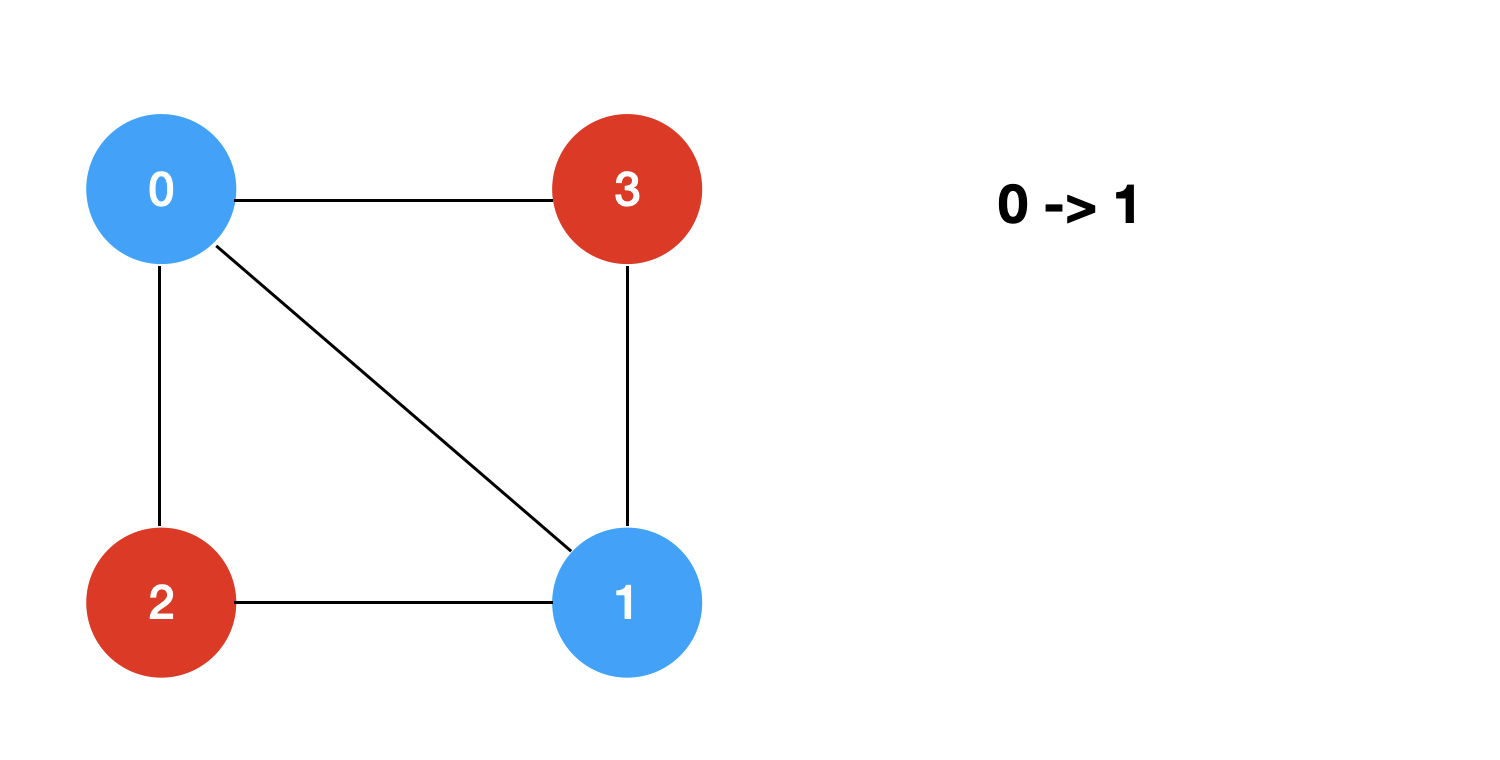
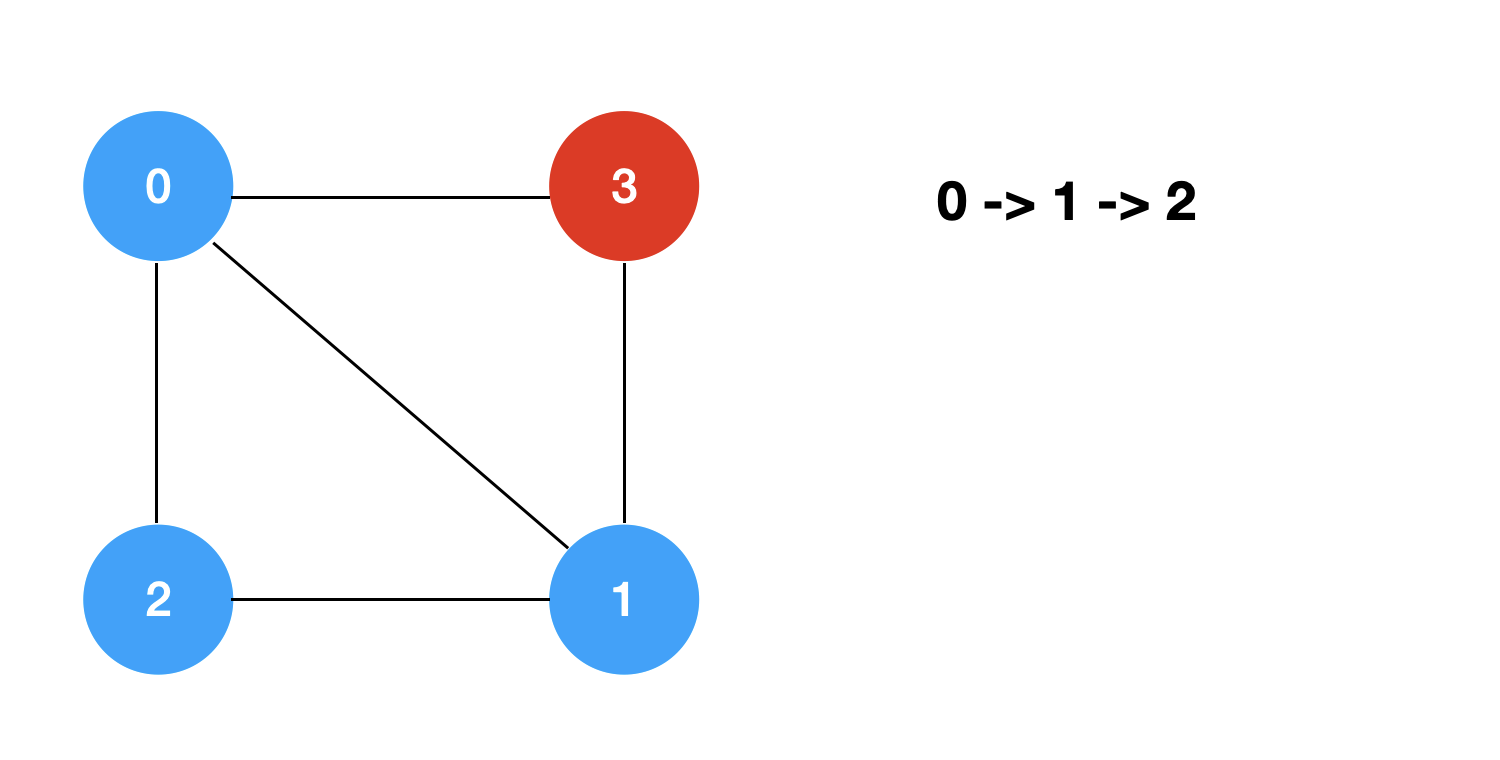
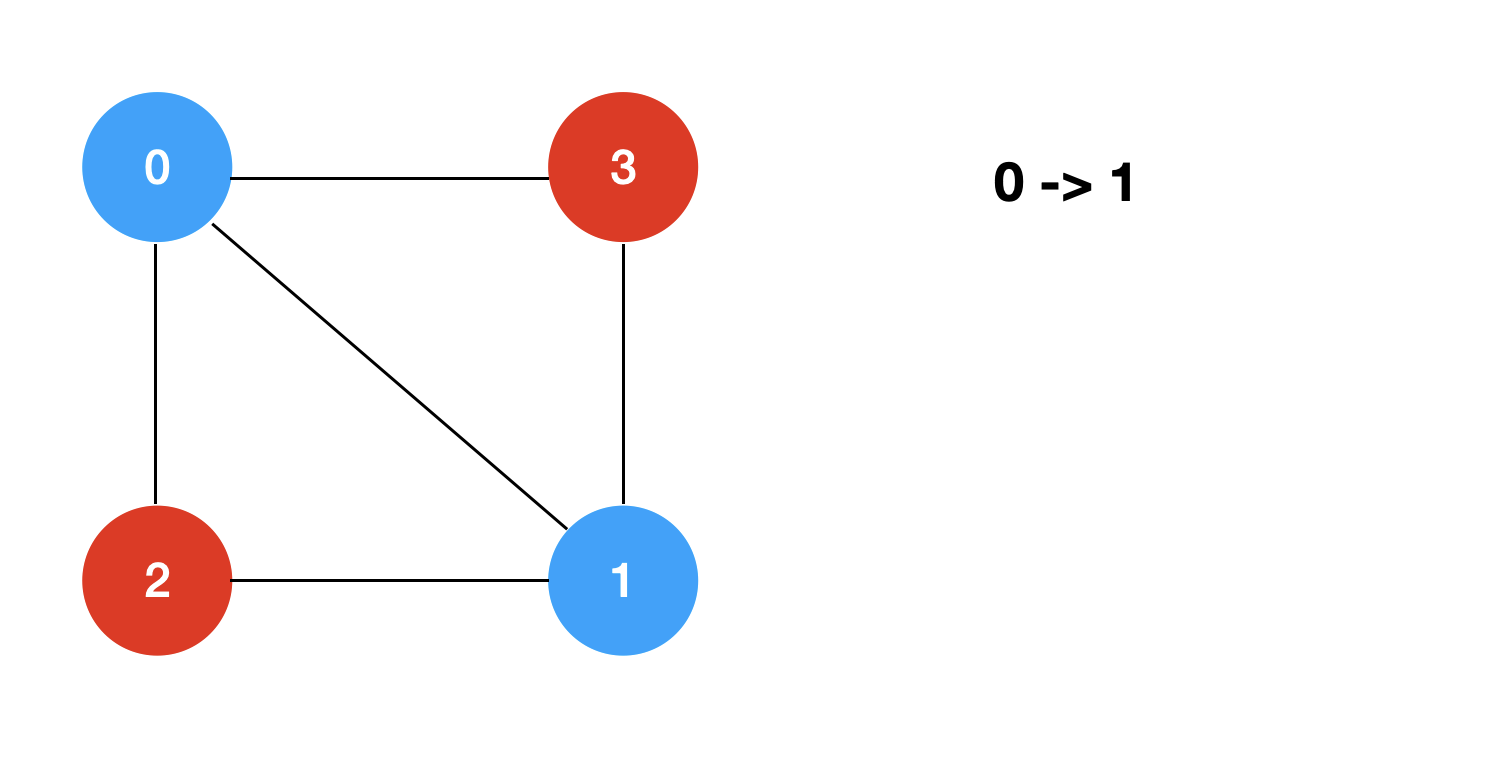
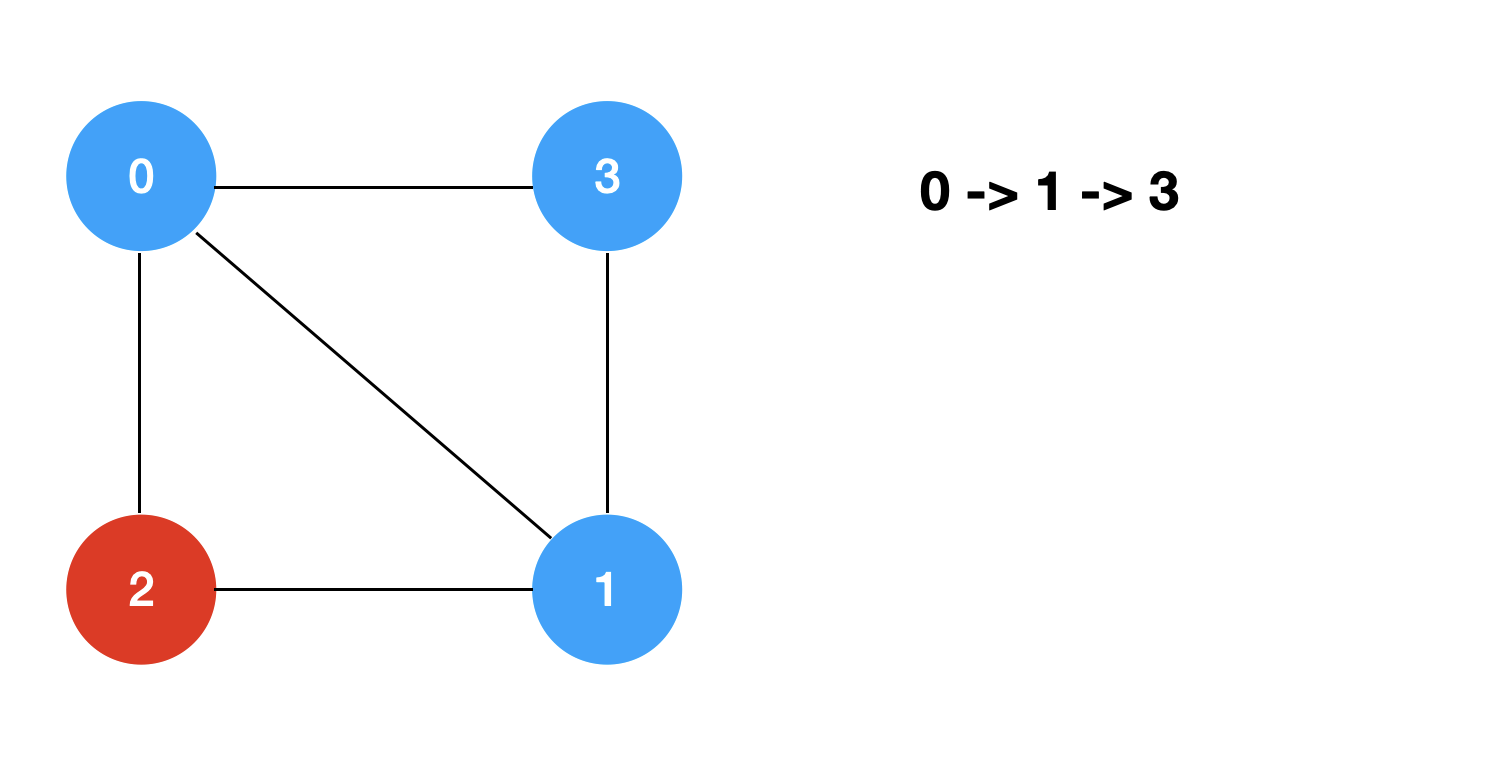
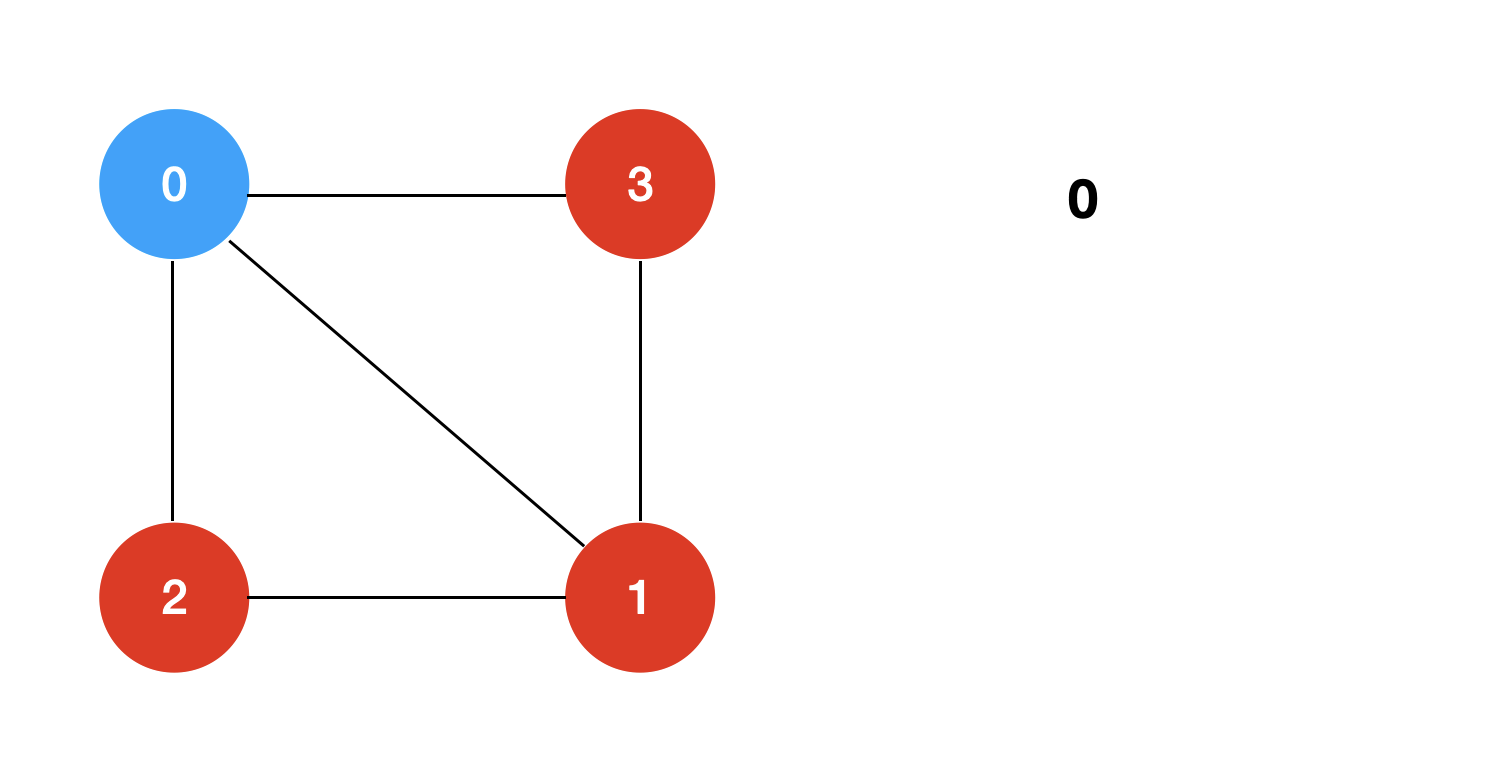
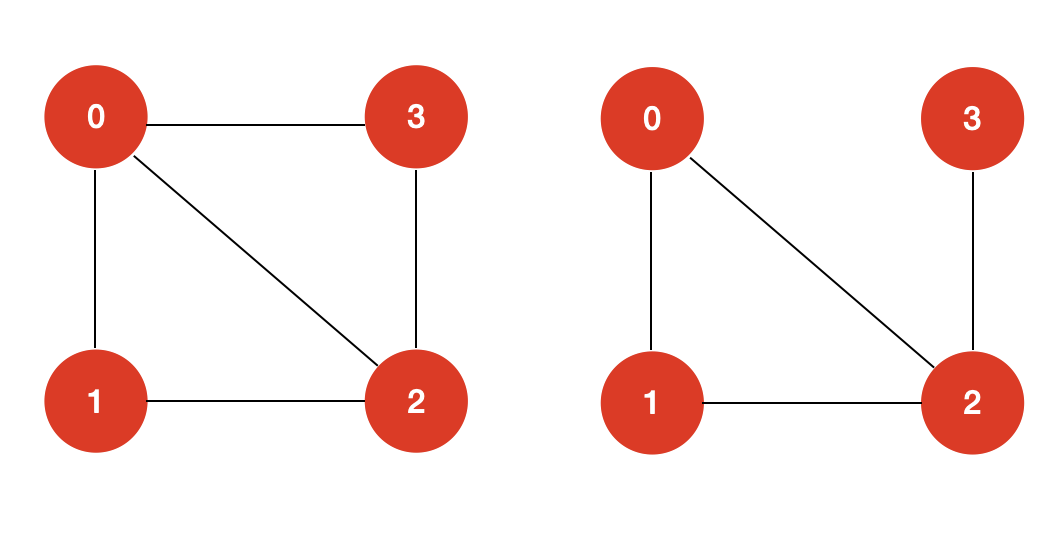
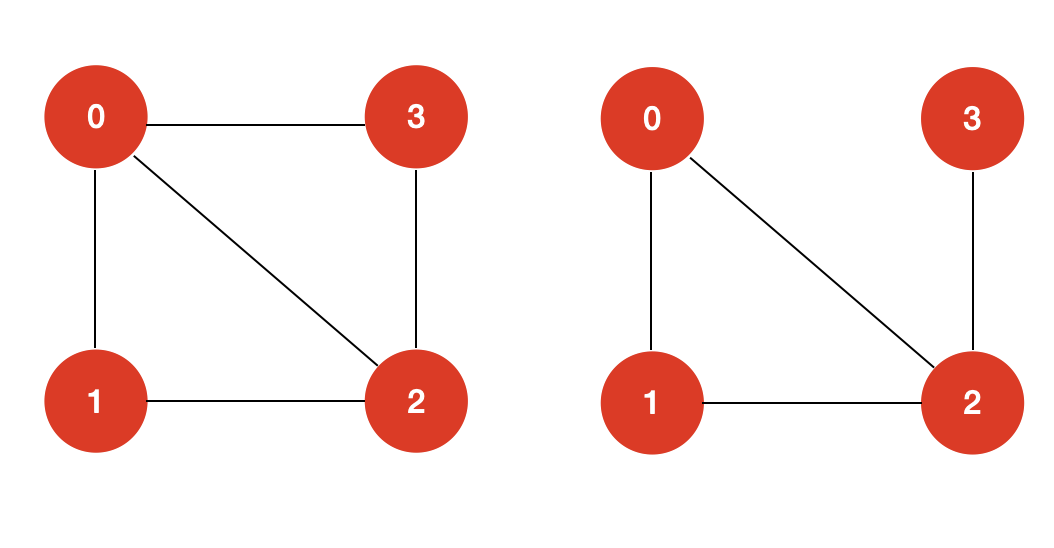
譬如上面这两个图,左图既存在哈密尔顿回路,也存在哈密尔顿路径。而右图只存在哈密尔顿路径,并不存在哈密尔顿回路。 二:求解哈密尔顿回路如何求解一个图是否存在哈密尔顿回路呢? 一个最直观的想法就是暴力求解。暴力求解的思路也很简单:我们遍历图的每一个顶点 v,然后从顶点 v 出发,看是否能够找到一条哈密尔顿回路。 暴力求解的代价同求解全排列问题是等价的,其时间复杂度为 O ( N ! ) O(N!) O(N!),N 为图的顶点的个数。 O ( N ! ) O(N!) O(N!) 是一个非常高的复杂度,它并不是一个多项式级别的复杂度。像 O ( 1 ) O(1) O(1), O ( N l o g N ) O(NlogN) O(NlogN), O ( N 2 ) O(N^2) O(N2) 这些我们常见的复杂度都是多项式级的复杂度,而 O ( a N ) O(a^N) O(aN), O ( N ! ) O(N!) O(N!) 这些复杂度是非多项式级的,也就是说,在数据量 N 极大的情况下,我们的现代计算机是不能承受的。 那么除了暴力求解哈密尔顿回路问题,是否存在更好的算法? 很遗憾的是,对于哈密尔顿问题,目前并没有多项式级别的算法。我们只能在暴力破解的基础上,尽量去做到更多的优化,譬如回溯剪枝,记忆化搜索等,但是,还没有找到一种多项式级别的算法来解决哈密尔顿问题。 通常,这类问题也被称为 NP(Non-deterministic Polynomial)难问题。 综上所述,求解哈密尔顿回路,我们可以采用回溯+剪枝的思想来进行求解。 对于这样一个图:
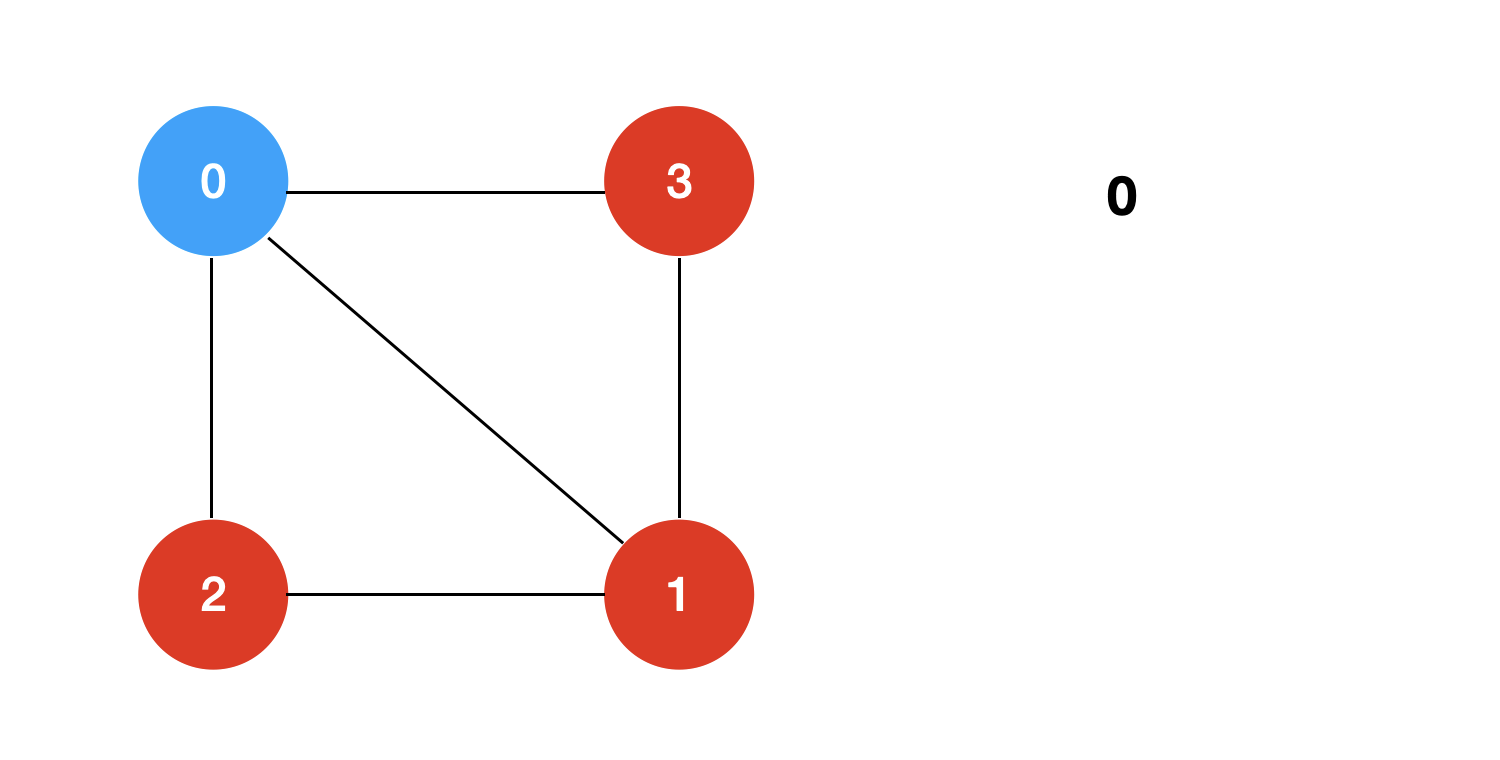
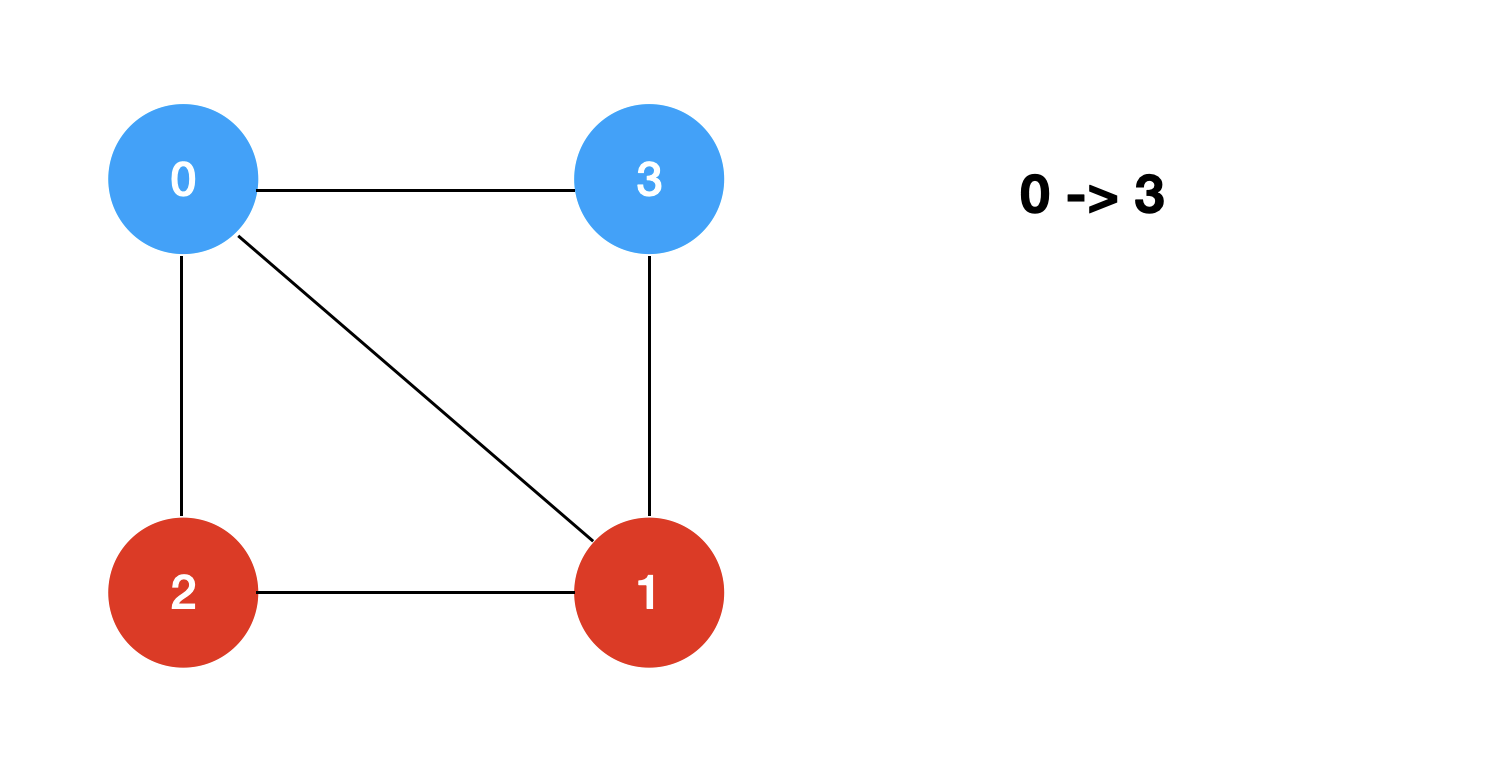
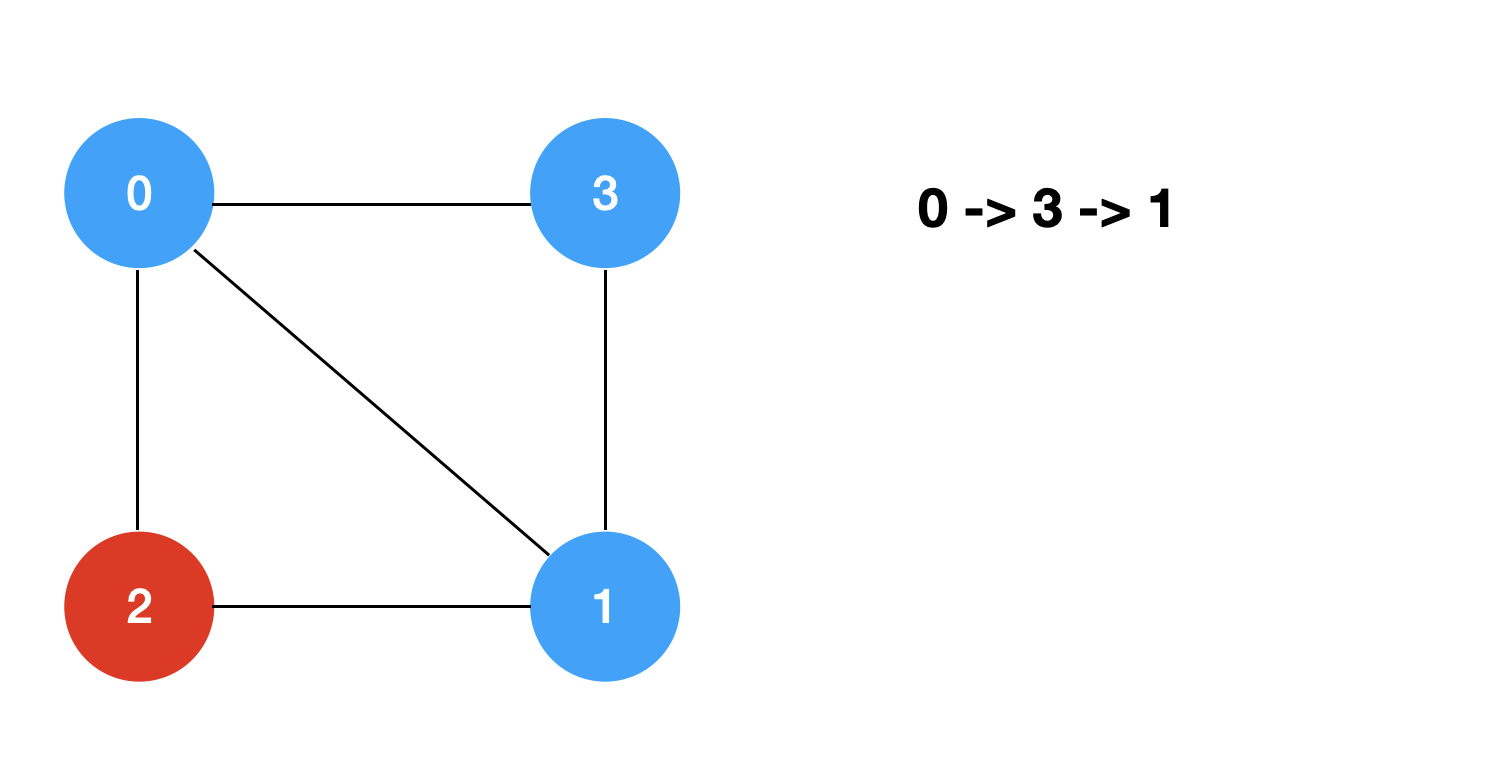
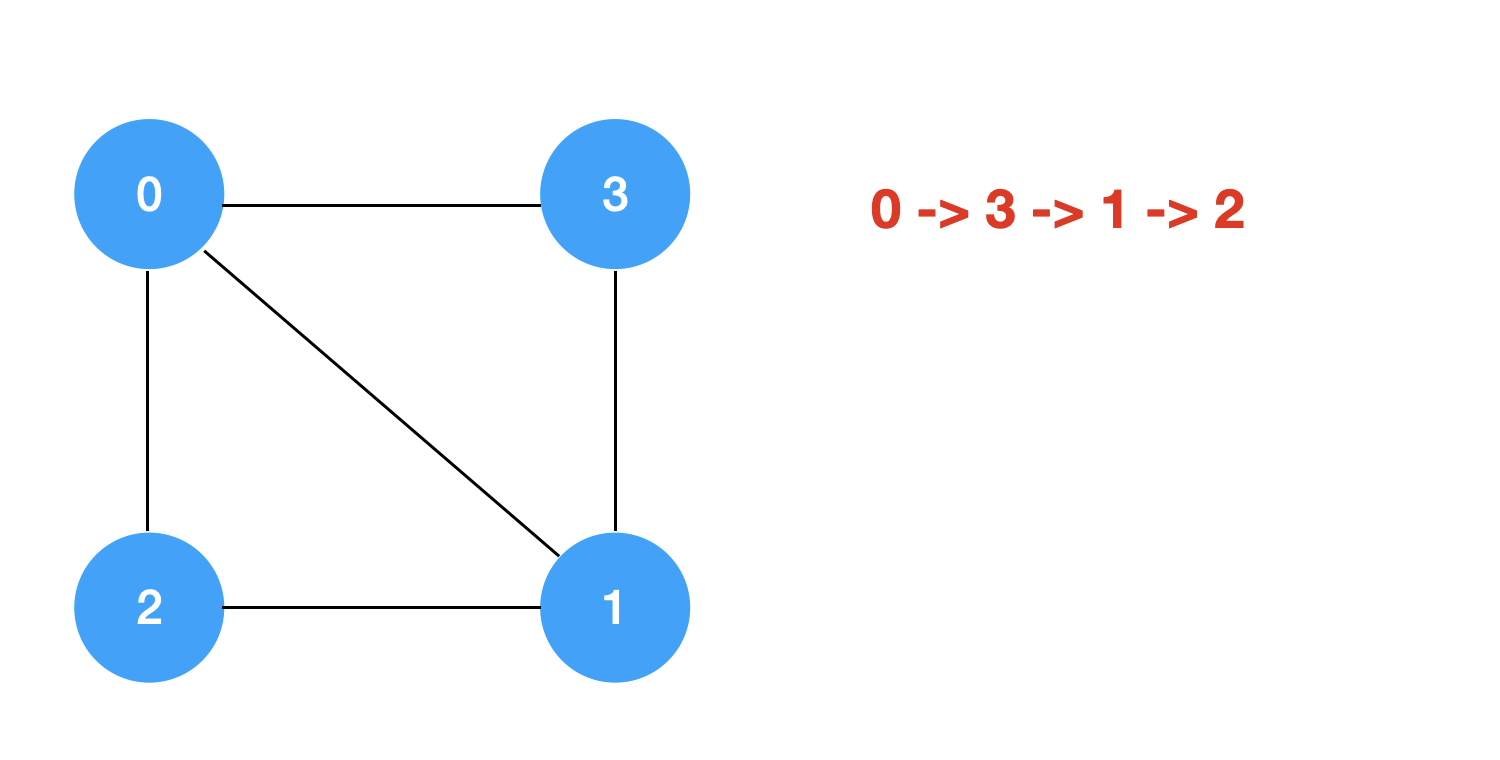
回溯+剪枝的过程模拟如下:
Java 代码: import java.util.ArrayList; import java.util.Collections; import java.util.List; public class HamiltonLoop { private Graph G; private boolean[] visited; private int[] pre; private int end; // 用来表示最后一个被遍历的顶点 public HamiltonLoop(Graph G) { this.G = G; visited = new boolean[G.V()]; pre = new int[G.V()]; end = -1; dfs(0, 0, G.V()); } /** * 对图进行深度优先遍历 * * @param v * @param parent * @param left 表示还有多少个点没有遍历 * @return */ private boolean dfs(int v, int parent, int left) { visited[v] = true; pre[v] = parent; left--; // 如果所有的点遍历完毕,并且起始点和终止点存在一条边 if (left == 0 && G.hasEdge(0, v)) { end = v; return true; } // G.adj(v) 为寻找 v 的相邻顶点 for (int w : G.adj(v)) if (!visited[w]) { if (dfs(w, v, left)) return true; } visited[v] = false; return false; } /** * 获取哈密尔顿回路 * * @return */ public List result() { List res = new ArrayList(); if (end == -1) return res; int cur = end; while (cur != 0) { res.add(cur); cur = pre[cur]; } res.add(0); Collections.reverse(res); return res; } }
对于这两个图进行测试,我的 HamiltonLoop 算法类输出的结果如下: 图1 [0, 1, 2, 3]图2 []因为图2 本身就不构成一个哈密尔顿回路,所以,其结果输出为空也符合我们的意料之中。 三:求解哈密尔顿路径求解哈密尔顿路径和求解哈密尔顿回路的算法整体框架是基本一致的。 对于求解哈密尔顿路径来说,起始点是谁很重要,同一个图,从有的起始点出发就存在哈密尔顿路径,从有的起始点出发就不存在哈密尔顿路径。所以,我们在算法设计中,构造函数需要用户显示地传入起始点。 我的求解哈密尔顿路径的算法类 HamiltonPath 的构造函数是这样的: // 用户需要在构造器中传入图 G 以及起始点 s public HamiltonPath(Graph G,int s){ // ... }除了这一点外,求解哈密尔顿路径只需要保证,从起始点开始,所有的点均被遍历到且仅被遍历一次,并不需要起始点和终止点之间有边。所以,在 dfs 的逻辑中,我们只需要改变递归的终止条件即可: // 不需要保证终止点 v 和 起始点 s 存在一条边,即: G.hasEdge(v, s) if(left == 0 /*&& G.hasEdge(v, s)*/){ end = v; return true; }整体的 Java 代码如下: import java.util.ArrayList; import java.util.Collections; import java.util.List; public class HamiltonPath { private Graph G; private int s; private boolean[] visited; private int[] pre; private int end; private int left; public HamiltonPath(Graph G, int s) { this.G = G; this.s = s; visited = new boolean[G.V()]; pre = new int[G.V()]; end = -1; this.left = G.V(); dfs(s, s); } private boolean dfs(int v, int parent) { visited[v] = true; pre[v] = parent; left--; if (left == 0) { end = v; return true; } for (int w : G.adj(v)) { if (!visited[w]) { if (dfs(w, v)) return true; } } visited[v] = false; left++; return false; } /** * 返回哈密尔顿路径 * * @return */ public List result() { List res = new ArrayList(); if (end == -1) return res; int cur = end; while (cur != s) { res.add(cur); cur = pre[cur]; } res.add(s); Collections.reverse(res); return res; } }
依旧是对这两个图进行测试,首先,我们传入构造器的顶点设置为 0。我的 HamiltonPath 算法类输出的结果如下: 图一 [0, 1, 2, 3]图二 [0, 1, 2, 3]从顶点 0 出发,左右两个图均存在哈密尔顿路径。 然后,我们将传入的顶点设置为 2。我的 HamiltonPath 算法类输出的结果如下: 图一 [2, 1, 0, 3]图二 []左图从顶点 2 出发存在哈密尔顿路径;右图如果从顶点 2 出发,则不存在哈密尔顿路径,我们的算法结果输出为空,这与我们的预期结果是保持一致的。 四:状态压缩在我们的代码中,一直都使用布尔型的 visited 数组来记录图中的每一个顶点是否有被遍历过。在算法面试中,对于像哈密尔顿回路/路径这样的 NP 难问题,通常都会有输入限制,一般情况下,求解问题中给定的图不会超过 30 个顶点。 这样,在算法笔试/面试中,我们就可以对 visited 数组进行状态压缩来优化算法类执行的效率。我们知道一个 int 型的数字有 32 位,每一位不是 1 就是 0,这正好对应了布尔型的 true 和 false。 所以,我们可以将 visited 数组简化成一个数字,该数字的每一个比特位用来表示 visited 数组的每一个 true 或 false 值。 来看一下我们的 HamiltonLoop 中 dfs 的代码: private boolean dfs(int v,int parent,int left) { visited[v] = true; // 待优化... pre[v] = parent; left--; if(left == 0 && G.hasEdge(0,v)) { end = v; return true; } for(int w : G.adj(v)) if(!visited[w]) // 待优化... if(dfs(w,v,left)) return true; visited[v] = false; return false; // 待优化... }我们的 dfs 中,涉及到 visited 数组的操作共三处,这三处我已经使用注释标注出来了。 现在,我们的目标就是使用一个数字来代替 visited 数组,如果 visited 是一个 int 型整数,那么这三处操作应该如何用位运算来表示呢? visited[v] = true; 如果我们使用整型数字来表示 visited,那么这处的操作就是将数字的第 v 个位置从 0 设置为 1,其位运算操作表示为: visited + (1 |
【本文地址】