数学思考：我们是怎样得出向量内积的坐标公式的？

您所在的位置：网站首页 › 向量中的夹角公式是什么 › 数学思考：我们是怎样得出向量内积的坐标公式的？

数学思考：我们是怎样得出向量内积的坐标公式的？

2024-07-09 16:47| 来源: 网络整理| 查看: 265

今天在做高数中关于三角函数的题，偶然用到三角函数的一个公式：

$\sin \left ( x+y \right )=\sin x\cos y+\cos x\sin y$

不禁让我想起当年高中时候痴迷于证明这个公式的各种方法（记性不好，导致现在都忘得差不多了哈哈），记得课本上给出了这样一种方法：

在xOy坐标系上画一个原点为圆心的单位圆，从原点出发伸出两个方向不同的向量 $\overrightarrow{a},\overrightarrow{b}$

保证两终点落在圆上（这样a,b模为一，这样做是为了推算方便，本身不是必要）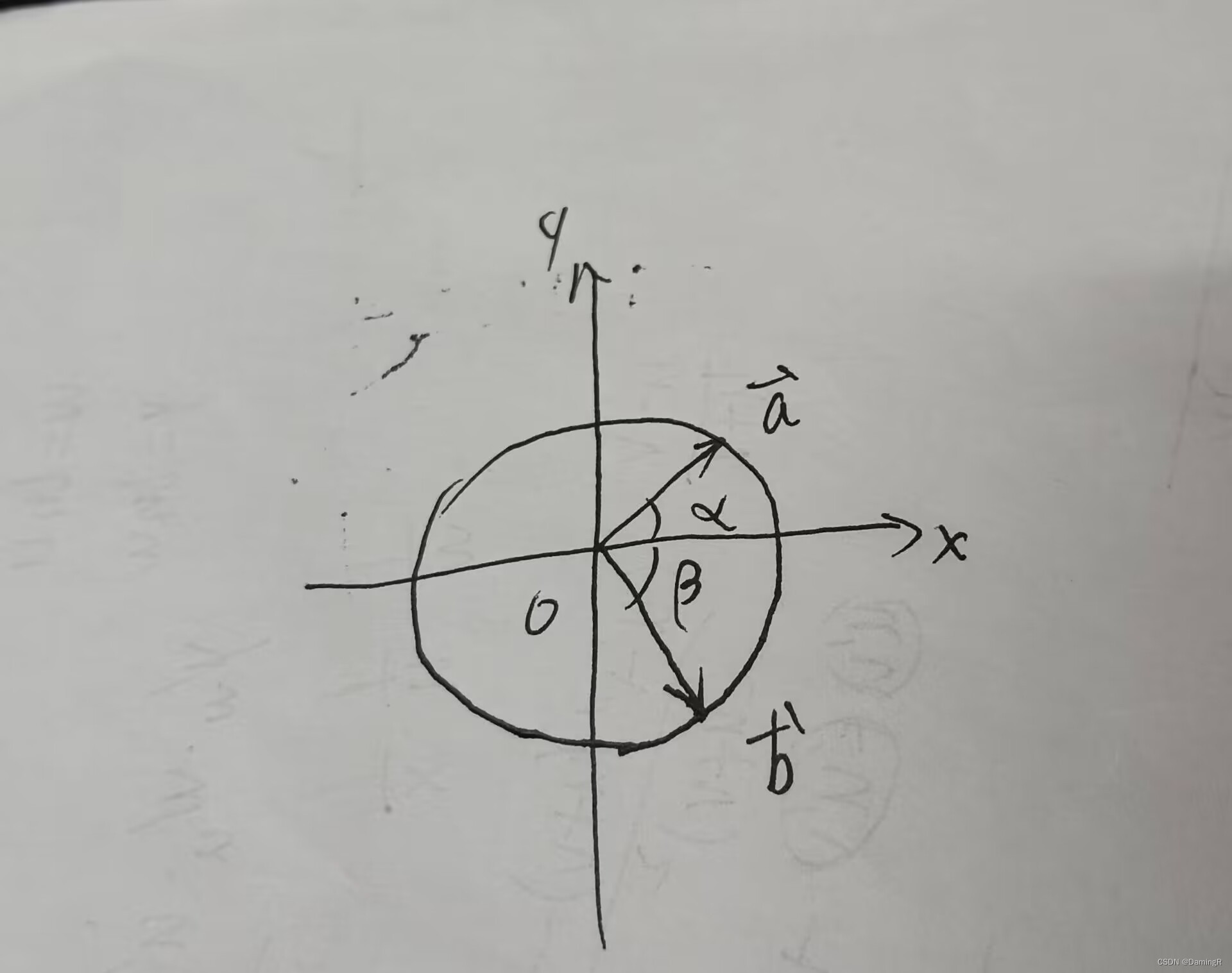

徒手画的圆，不得不说比我当年高考时候画的丑多了

我们知道两个向量的内积（或者叫数量积）有两个公式：其一便是经典的定义式

$\overrightarrow{x}\cdot \overrightarrow{y}= \left \| \overrightarrow{x} \right \|\left \| \overrightarrow{y} \right \|\cos \overrightarrow{x},\overrightarrow{y}$

cos里面那个就是向量x与y的夹角。

而后面（我指的是刚学向量那时候）我们知道向量可以用坐标表示，于是就有了内积的坐标写法：

$\overrightarrow{x}\cdot \overrightarrow{y}= X_{x}X_{y}+Y_{x}Y_{y}$

X和Y就是相应的横坐标和纵坐标。

回到上面的图，向量a和向量b长度都是1，这意味着对上面两个公式有：

$\left \| \overrightarrow{x} \right \|=\left \| \overrightarrow{y} \right \|=1$

以及

$\begin{pmatrix} X_{x} & X_{y}\\ Y_{x}& Y_{y} \end{pmatrix} = \begin{pmatrix} \cos \alpha & \cos \beta \\ \sin \alpha & \sin \beta \end{pmatrix}$ （别问，问就是方便）

于是，当我们把这两个式子联系起来的时候，会出现

$\cos \overrightarrow{x},\overrightarrow{y} = \cos \alpha \cos \beta + \sin \alpha \sin \beta$

因为向量x与y的夹角就是

$\alpha -\beta$ （这里beta是负数，规定逆时针角为正）

因此 $\cos \left ( \alpha -\beta \right ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$

一个震惊世界（大概不会，但当时确实震惊到我）的公式诞生了！

等等。。。

扯了这么多，到底要说明什么呢？

数学的奥妙之一在于一个简洁的公式背后包含着海量的信息。回顾前面的推导，最开始的时候我们只用到了两个等式：

$\overrightarrow{x}\cdot \overrightarrow{y}= \left \| \overrightarrow{x} \right \|\left \| \overrightarrow{y} \right \|\cos \overrightarrow{x},\overrightarrow{y}$

$\overrightarrow{x}\cdot \overrightarrow{y}= X_{x}X_{y}+Y_{x}Y_{y}$

定义式自不必说，关键第二个式子，似乎我们在学的时候从来没有关注过它是怎么得出的（印象中书上给出了推导过程？？）而正是通过他得出上面三角函数公式，换言之，他是式子中最关键的一环。那么到底他是怎么来的呢？

学过高数的都知道（），向量的坐标表示源于正交基分解。所谓正交基，就是在坐标轴选取三个（当然xOy平面是两个）两两垂直且长度为1向量，称为基底。这样坐标系中任何一个向量都可以用基底来线性表示（问线性表示是什么的，我保你高数必挂）也就是

$\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$

当在平面中，只需要两个基底（多了没用）

$\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$

因为点的坐标跟向量坐标一一对应，这才使得点的坐标形式与向量联系起来

$x\overrightarrow{i}+y\overrightarrow{j}= \left ( x,y \right )$

好的，相信对向量掌握足够的已经跳过这些内容了，但回顾一下还是很有必要的。接下来用这个坐标分解，也就是基向量来推出向量的内积表达：

$\overrightarrow{a}=x_{1}\overrightarrow{i}+y_{1}\overrightarrow{j}$

$\overrightarrow{b}=x_{2}\overrightarrow{i}+y_{2}\overrightarrow{j}$

$\overrightarrow{a}\cdot \overrightarrow{b}=(x_{1}\overrightarrow{i}+y_{1}\overrightarrow{j})(x_{2}\overrightarrow{i}+y_{2}\overrightarrow{j})$

$=(x_{1}\overrightarrow{i}x_{2}\overrightarrow{i}+x_{1}\overrightarrow{i}y_{2}\overrightarrow{j}+y_{1}\overrightarrow{j}x_{2}\overrightarrow{i}+y_{1}\overrightarrow{j}y_{2}\overrightarrow{j})$

而向量与他自身的乘积等于模平方，基底模为1，相垂直的向量因夹角 $90^{\circ}$ 乘积为0

这样原式子只留下x1x2和y1y2,于是得出

$\overrightarrow{a}\cdot \overrightarrow{b}=x_{1}x_{2}+y_{1}y_{2}$

这是从“数”的角度理解 $\cos \left ( \alpha -\beta \right )$ 的本质。那么从“形”呢？

这就不得不又双叒叕。。拖出上面的草图

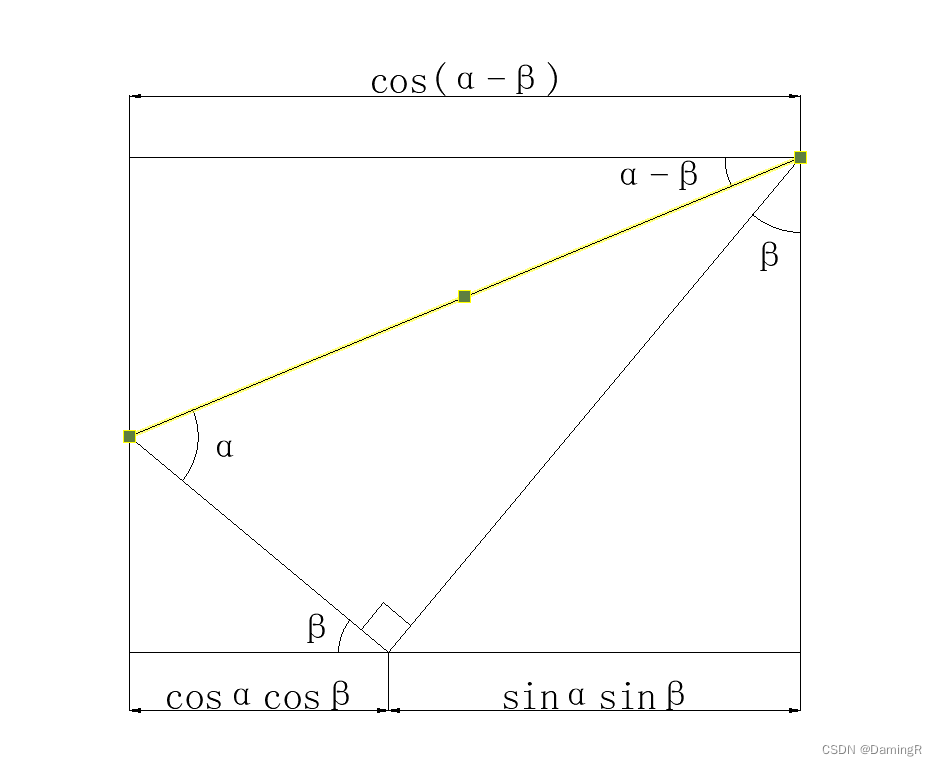
错了，其实是下面这个图：

简明扼要，一目了然（喜）

今天的分享就到这里，本来只是有感而发，回头一看都写了这么多了。。。大佬们就点个赞，加个关注再走吧。。。

【本文地址】

数学思考：我们是怎样得出向量内积的坐标公式的？

数学思考：我们是怎样得出向量内积的坐标公式的？

今日新闻

推荐新闻