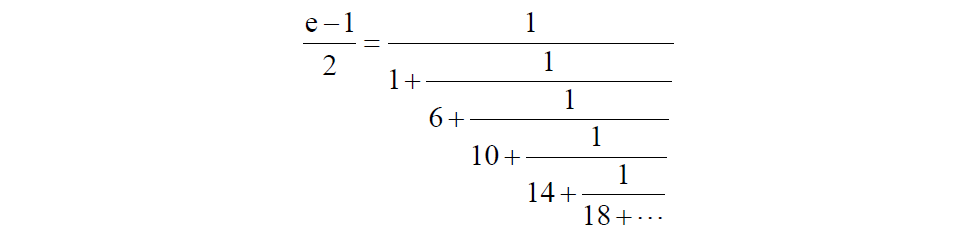欧拉数的推导史(自然对数底e)

(The History of the Derivation of Euler’s Number)

摘要

本文按时间顺序(chronological)总结了许多鼓舞人心的(inspiring)辛勤工作的数学家的作品，他们在数学领域辛勤耕耘，带来了欧拉数的收获，也被称为Napier数或更“臭名昭著”地称为e(自然对数底)。

关键字

欧拉数，Napier数，数学史

目录

1. 引言

2. 数e首次出现在数学中是得益于John Napier在他的对数工作中的努力——1618 年

3. 伦敦Gresham学院教授Henry Briggs开始研究Napier的工作，并确定了以10为底的e的对数的数值运算——1624年

4. Saint Vincent计算等轴双曲线(Rectangular Hyperbola)下的面积——1647年

5. 惠更斯(Huygens)理解了Saint-Vincent发现的矩形双曲线与对数之间的关系——1661年

6.  Nicolaus Mercator出版了Logarithmotechnia(对数法)，这是一部出色的作品，其中包含 log(1 + x) 的级数展开——1668年

7.  雅各布·伯努利(Jacob Bernoulli)最终“发现”了数 e，不过不是通过对数，而是通过复利发现——1683年

8.  莱布尼茨(Leibniz)写给惠更斯(Huygens)的一封信，正式陈述数 e 的值，但使用字母 b 代替——1690年

9.  约翰·伯努利 (Johann Bernoulli) 着手研究涉及指数函数的微积分——1697年

10.  Leonhard Euler 继续指定用字母e 来表示这个数——1731年

11.  Leonhard Euler 继续就 e 做出各种发现——1748年

12.  Hermite 正式证明e是一个非比率数(Irrational Number)——1873年

13.  Boorman 计算e到 346 位小数——1884年

14.  总结

数 e，众所周知的欧拉数，是非比率数(无理数)之一，类似于“臭名昭著(infamous)”的π。 与π 相比，它是一个相对年轻的非比率数，在 16 世纪中期首次出现在计算中 [1]。

在随后的岁月里，这个非常有趣的(intriguing)数e 仍然隐藏在早期数学家的复杂计算中，它的存在和重要性质像被什么东西笼罩着(shrouded)，因为当时的数学家们更紧迫的问题是找到其他不那么抽象但更实用的物理和数学解决方法，以解决诸如导航等问题[2]。

18 世纪初，Leonhard Euler在他的一封信中首次提到了数e。这是数学人所知的第一次用e 称呼这个数，在此致谢Leonhard Euler，他确定了e的独特属性，这个独特属性使其成为了一个非比率数 [3]。

在接下来的几年时间里，e得到了进一步研究，但没有像数学家对π那样热情。欧拉数，以及其他非比率数，是大自然展现人类的好奇心和人类探索未知的力量的无限性的一种独特方式 [4]。

多年以来，宇宙的奥秘一直隐藏在奇怪而有趣的数学“结构(fabric)”中。在这个世界上，除了少数极具数学天赋的人之外，数学似乎更像是一种抽象现象，但它比人们想象的更深入地融入每个人的日常生活中。

毫无疑问，非比率数可能是数学中最迷人的(fascinating)奇迹(wonder)。作为一个简单的定义，可以说非比率数永远不能用数字表示其有限，它们的有效数字会扩展到无穷大。 换句话说，它们会永远持续下去 [5]。 一些例子包括著名的π、黄金比例(Φ)甚至一些数字的简单平方根，例如2的平方根()

。 然而，本文将主要讨论的非比率数是一个与商业、计算和几乎所有其他源自数学的学科交织在一起的数——欧拉数e。

Merchiston 的 John Napier(见图 1)是一位苏格兰地主。他还以数学家、敏锐的物理学家(keen physicist)和天文学家(astronomer)而闻名。 John Napier 最著名的发现是发现了对数并进行了对数计算工作 [6]。 在他的时代里，他看到涉及非常大的数字和非常小的数字的计算是一项艰巨的任务。作为一个坚信数学总是必须应用于现实生活的务实的人，他首先开发了一种对数系统，这成为已知最早的对数。

今天，从本质上讲，对数通过将巨量的(extensive)乘法任务简化为仅靠将两个数字相加即可获得与用乘法计算得出的结果相同的值，从而简化了海量的计算。换句话说，对数是计算指数的捷径。John Napier的目标基本上就是这个，所以他在发现对数后继续开发，做出了世上第一个对数系统，该系统遵循下面简要描述的过程。

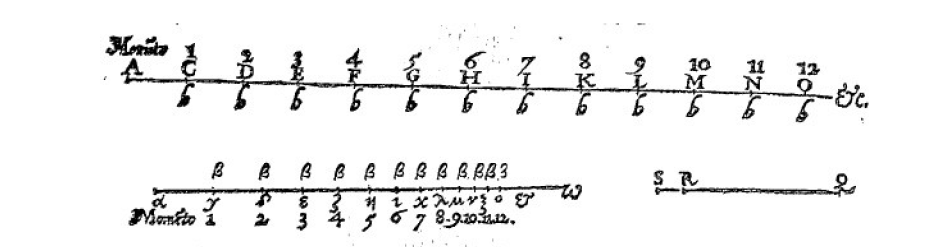
--------------------------------------------图1 John Napier (1550-1670)----------------------------------------------

将每个数与一个代表数关联。Napier最初将这个代表的数称为“人造数(artificial number)”(一段时间后他将其称为“对数(logarithm)”,与真数对应的数，两个数成对出现)。其主要思想是，当这两个代表数“相加”(或相减)时，其结果将等同于两个原始数相乘或相除时的结果(见图2)。

---------图2 John Napier用于移动质点(particles)的两条原始平行线---------------

Napier在1614年出版的(奇妙对数法则说明书)中展示了他关于对数的原创作品。数e首次在这部作品中隆重亮相，但没有正式识别出其独特特性的原本。Napier最初的对数与今天使用的对数不太相似。这些旧对数以() 为底，计算还涉及一个常数()。Napier将他发现的对数定义为几何形式的两个距离之比(注：用几何来展示对数的这种特性)。然而，今天使用的对数是基于指数的概念。 Napier 的计算在今天可能没有被广泛使用，但对Napier的工作有清晰的认识有助人们掌握 e 与 Napier 的工作和对数的早期关系的概念(见图 3)。

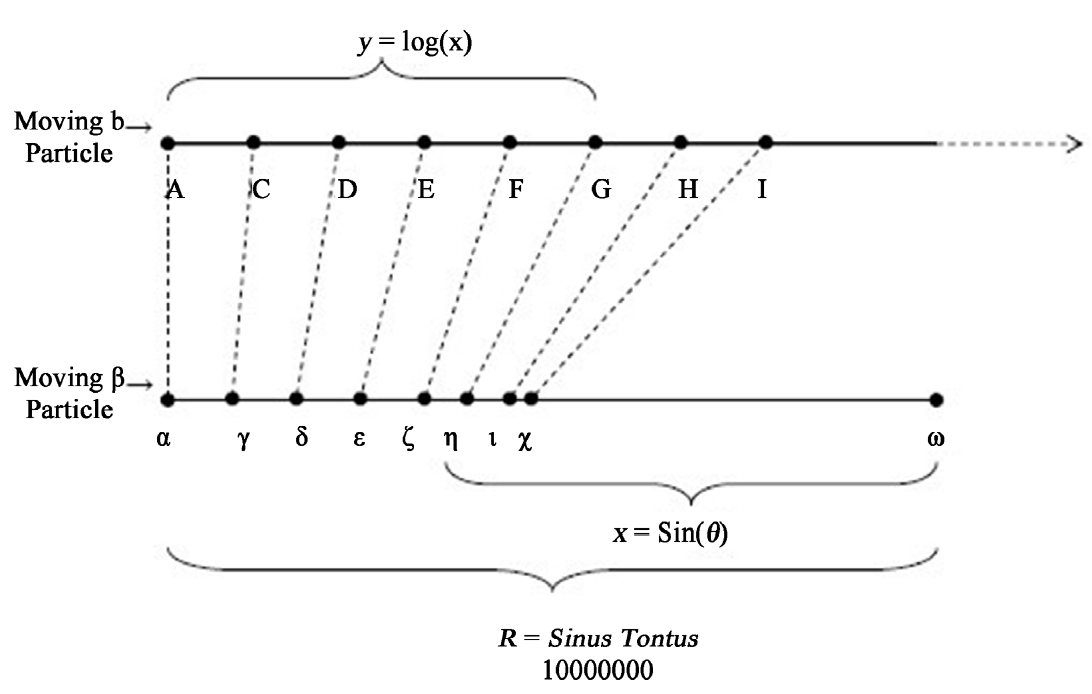
---------图3 两条线与对数和正弦函数之间的关系。可以清楚地看到这两个质子及其行进路线。---------------

Napier将他的对数思想建立在一个以运动学为主的(kinematic)框架中。他首先想象两个质子，他将其中一个质子设置为在一条无限直线上以恒定速度运动，以固定的时间间隔移动相同的距离。他设置的另一个质子以与第一个相同的时间和速度移动，但是这个粒子必须移动的线的长度是有限的。它在特定点的速度与其路径中剩余的距离成正比 [7]。

Henry Briggs(见图 4)是伦敦Gresham学院的教授。Napier发表了他的对数著作后，Briggs开始研究它，并发现了一种关系，从而导致以 10 为底的对数的发现。Briggs对对数在航海中的应用非常感兴趣，这在当时对英国来说是一个非常重要的领域。他的主要工作是计算以10为底的e对数的数值运算。 然而，Briggs 从未对任何诸如e这样的数进行任何具体引用 [8]。

----------------------图4 英国数学家Henry Briggs(1561-1630)---------------------------------------------------

Grgoire de Saint-Vincent(见图 5)是一位著名的佛兰芒(Flemish)(佛兰芒是指比利时西北部一部分)数学家。他的研究和工作，主要是关于双曲线的求积，这是他在数学史上被铭记的原因。矩形双曲线是按下面表达式在笛卡儿坐标轴上给出的任何曲线

xy = k 。

Saint-Vincent发现，矩形双曲线与区间[p, q]围成的区域的面积与曲线与另一个区间[r, s]围成的面积相等，只要满足条件  。

他是否认识到与对数的联系仍然不确定，因为没有提供他的任何计算的直接证据。 即使他确实包括了广泛的计算，他清楚地遇到数字 e 的可能性也很低 [9]。

----------------------图5 Gregoire Saint Vincent (1584-1667)-----------------

著名的荷兰人克里斯蒂安·惠更斯(Christian Huygens)(见图 7)是他那个时代备受尊敬的数学家、发明家和天文学家。许多人认为他是有史以来最伟大的科学家之一，也是科学革命中的重要人物。令人着迷的是，他还是Saint-Vincent的学生。Huygens在他对等轴双曲线(rectangular hyperbola)的研究中，建立了Napier发现的对数与Saint-Vincent发现的等轴双曲线之间的关系。

前面提到过，等轴双曲线是在笛卡尔轴上由xy = k给出的任何曲线。Huygens注意到一个有用的性质，从双曲线来看，等轴双曲线下的面积在区间[p, q]和区间[r, s]围成的面积相等，只要满足条件  。Huygens明确地考察了等轴双曲线 xy = 1下面积与本质上是以e为底的自然对数之间的关系(见图6)。

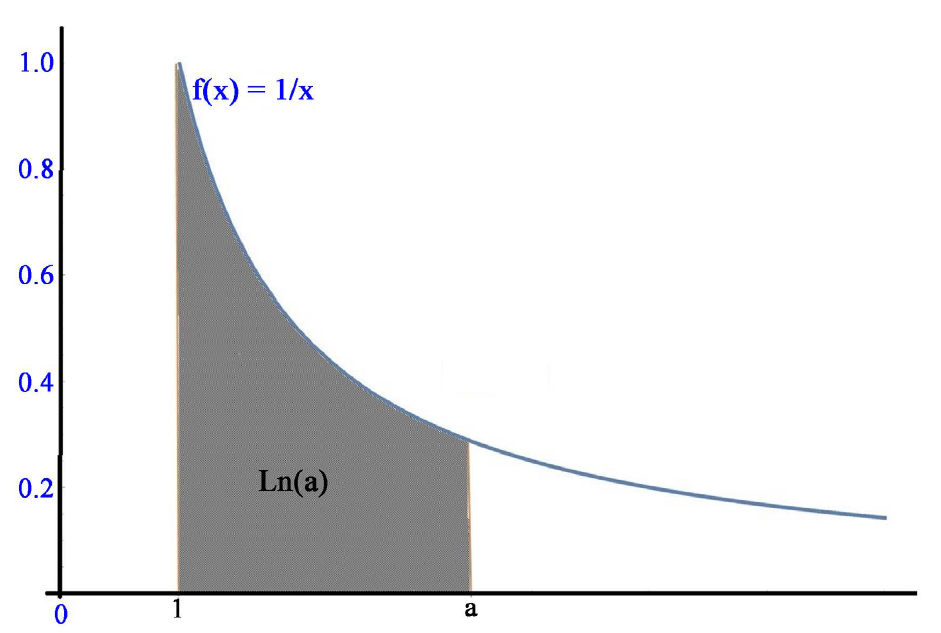
----------------------图6 这里显示的是一个等轴双曲线。以灰色突出显示的是从1到 a 的曲线 下方的区域。如果a小于1，则a到1的面积算负数。-------------

A(xy) = A(x) + A(y)

这种函数属性使对数独一无二，通常将此类函数A(x) 称为对数。值得注意的是，当选择等轴双曲线xy = 1时，就获得了以为e为底的对数——也称为自然对数。

同样，从这里可以清楚地识别出e的以10为底的对数，它由Huygens计算到小数点后 17位。最后，e在历史上出现了第一次重大现身。但是，它在Huygens的工作中只是被认为是另一个数，作为一个非比率数并没有太大的意义。唯一的原因是e的独特性质尚未被发现。再一次，这离找到非比率数很近，但e仍然未被识别，并被其他思想所掩盖 [5]。

---------------图7 Christiaan Huygens (1629-1695) -------------------------

Nikolaus Mercator (参见图8)是一位德国数学家，因其发表的(对数法)的著作而闻名(参见图9)。在Mercator的著作 “对数法”中，Mercator首次将所有以 e 为底的对数标为“自然对数(natural logarithm)”。 同样，遗憾的是，奇特的数字 e 仍然只是另一个非比率数，并没有因其独特性而受到重视。 它在拐角处难以捉摸地等待着另一个聪明的头脑将它带入光明。他使用了 log(x + 1)的级数展开。

--------------------------------------图8 Nicolaus Mercator (1620-1687) ----------------------------------------

--------------------------------------图9 墨卡托的原著——对数法 -------------------------------------------------

著名的Bernoulli(见图 10)家族有许多成功的数学家，但Jacob Bernoulli是其中最成功的一位。他对微积分的多项贡献使他在数学界广为人知。事实表明，他也是第一个确定非比率数 e 的基本性质的数学家。

e的发现令人着迷的地方在于，尽管对数进行了大量的工作和研究，但以前的数学家并没有在这些对数计算过程中识别出数e。 事实上，这是两个完全不同的领域；通过Jacob Bernoulli 关于复利的研究，e最终被“发现”了。

Jacob Bernoulli于1683年在研究有关复利的问题时偶然发现了数e。

他的主要研究基于复利的问题，并探索连续复利的性质。他在寻找极限  

的答案。根据他使用二项式定理(binomial theorem)[10] 的计算，极限一定介于 2 和 3 之间。下面将解释类似于他的复利计算的扩展。

想象一下，一个银行账户的初始存款总额为 1.00 美元，每年支付 100% 的利息。在第一笔利息记入帐户后，该帐户的余额将在年底时计算为 2.00 美元。Bernoulli心中的问题是，如果银行提供的利息在下一个财政年度更频繁地记入帐户，会发生什么情况？

Bernoulli计算出，如果利息在任何特定年份记入两次，则利率为 50%，为期 6 个月。 结果，开户时的 1 美元每年乘以 1.5 两次，使银行账户的余额为：

 (美元)

如果采用类似的方法，但现在利息按季度计复利，它将产生

 (美元)

假设利息每月计复利会产生

  (美元)

如果采用 n 个复利时间范围和间隔，则可以通过将 100% 除以n个时间范围来计算每个间隔的利息，这会在财政年度结束时产生余额为 (1 + 1/n) 的总账户自乘以n次，即得到   。

 Bernoulli发现，当n 接近一个非常高的值时，序列达到一个特定的数。当每周计算复利间隔时，年末账户的余额为 2.692597 美元。 当时间范围进一步缩短至每日间隔时，它在本财年末的收益率为 2.714567 美元。

在采取非常小的时间间隔后，伯努利发现序列极限接近 2.7182818美元的值 [7]。 这在数学史上可以作为e的一阶近似。另外，这也可以说是数学史上第一次用极限过程来定义一个数，并且用这个极限过程定义了e。当时Bernoulli并没有意识到他的工作与对数的工作有关。

------------------------------------------图10 Jacob Bernoulli (1655-1705)------------------------------------

Gottfried Wilhelm Leibniz(见图 11)是他那个时代著名的德国数学家、逻辑学家和哲学家。他也是Christiaan Huygens的物理系学生。

     Leibniz 1690 年写了一封信给另一位数学家Huygens。在这封特别的信中，Leibniz用字母 b 表示现在称为 e 的数。 这可以看作是 e 第一次单独作为一个奇特的数出现。 最后，经过无数数学家几十年的计算，数e终于被赋予了属于它自己的标识或名称。尽管不是今天使用的现名，但至少，它是公认的。

Leibniz在他的微积分和积分过程中遇到了e。他的工作是在艾萨克·牛顿(Isaac Newton)的同一时期完成的，关于哪位数学家是微积分之父的争论仍在继续。

---------------图11 Gottfried Wilhelm Leibniz (1646-1716)----------------------

Johann Bernoulli(见图 12)是瑞士著名的伯努利家族的数学家。他的主要工作包括将微积分应用于机械问题。

早些时候，有人指出，由于数学界不将对数视为函数，因此存在一些问题。Johann Bernoulli于1697年开始研究指数函数的微积分，该微积分发表在他的著作《指数计算原理》(Principia calculi exponentialium seu percurrentium)中。这项工作使用逐项积分的冗长过程来计算许多指数级数。 这个微积分涉及数e和对数。在数学史上不同寻常的是，伯努利家族在 17 世纪末和 18 世纪初的几代人中共产生了6位杰出的数学家(见图 13)。

Johann Bernoulli是一位名副其实的重要数学家，不仅在与指数函数相关的微积分方面，而且在其他领域都有许多发现，例如解决最短时间问题(brachystochrone problem)，在该问题中，无法确定在引力场中的两个质子在两个函数之间下降的最快路径；以及其他数学贡献 [10]。

 ----------------------------------------图12 Johann Bernoulli (1667-1748)-----------------------------------

----------------------------------图13 Johann Bernoulli和Jacob Bernoulli在一讨论数学问题------------------

Leonhard Euler (见图14)仍然是瑞士最受尊敬的数学家、地理学家、工程师和天文学家之一，为科学和数学做出了无数发现。

Leonhard Euler对数学界做出了大量的数学贡献，这并没有让人们感到那么惊讶，因为发现今天使用的表示法——e——表示非比率数的符号是欧拉的贡献。然而，使用字母e 可能并不完全正确，因为它是他名字的第一个字母。 e甚至可能不是从单词“exponential”的第一个字母派生出来的。当时欧拉在他的研究中已经将符号a赋给了另一个数，他用字母e，即a后面的元音来表示和表示欧拉的数e。不管是什么原因，正如欧拉在 1731 年写给哥德巴赫的一封信中所使用的那样, 最终将e分配给这个数[2]。

---------------------------------------图14 Leonhard Euler (1707-1783)--------------------------------------------

Leonhard Euler在随后的几年中针对e 的性质做出了多项发现，并于1748年在 (无穷小分析导论)中发表了他的研究成果，并对与 e相关的独特性质和想法进行了正式的详细解释。特别地，欧拉证明了

同时也证明了Jacob Bernoulli的著作中表明 e 的第一个主要的近似值

 。

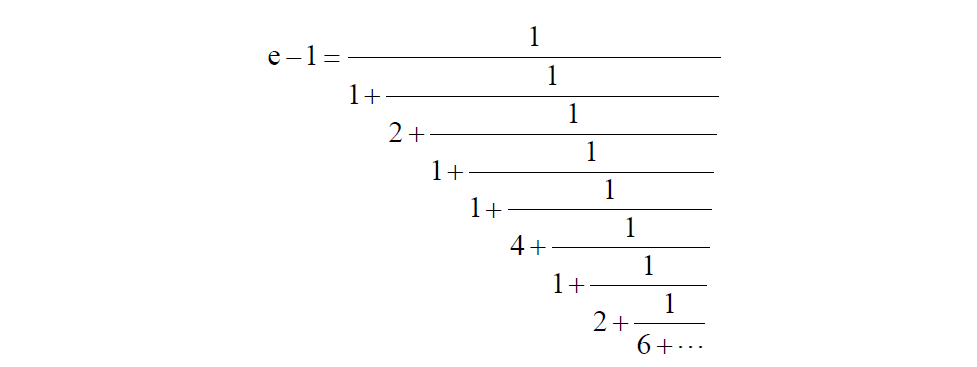
在这部著作中，Euler给出了数 e 到小数点后 18 位的近似值

e  = 2.718281828459045235 。

他是如何将 e 推导到小数点后18位的，这仍然是一个谜。他列出了它，但没有显示任何关于它是如何完成的计算。 最适用的解释是大约是采用等式

中的前20项进行计算。这给出了e的答案，其准确度与Euler所说的相同。

Euler发现的 e 的另一个迷人特征是复指数函数与正弦和余弦函数之间的联系。 Euler使用 De Moivre 的公式成功地推导出了这一点。

有趣的是，Euler还给出了e的连分数展开式，并表明随着计算的传导(propagated)存在一种模式。 特别地，他表明

在其中可以观察到

Euler在他的工作中提供了他发掘的(spotted)模式继续存在的证据。 尽管如此，他知道，如果发现某种形式的计算表明他展示的计算是无限的，这将作为 e 是非比率数的证据。

这很清楚，因为分数  

的传导计算遵循所观察到的这个模式，例如，6，10，14，......。很显然，e不可能是一个比率数。这个简单的计算得出的结论是，这可能是数学家首次尝试证明e的非比率性 [9]。

Shanks和 Glaisher 的工作是将e的值计算到小数点后 205 位——1854 年，数学家对计算e的小数位数的兴趣和动力并不像他们当时对 π 的热情那样强大和鼓舞人心[2]。

有几个人确实计算了它的十进制展开。 1854年，Shanks给出了e的大十进制展开式。 有趣的是，Shanks更热衷于将 π 计算到大量小数位。 Glaisher 在他的计算中表明，Shanks 计算的前 137 位 e 是正确的，但发现第 138 个值有错误，经过 Shanks 更正后，e为小数点后205位。当时试图解决该问题的数学家需要大约 120 项的

并需要付出巨大的耐心才能达到这种程度的准确性[1]。Benjamin Peirce 将数 e、π 和虚数 i——1864 Benjamin Peirce(参见图 15)在他的一次演讲中对他的学生说：

Gentlemen, that is surely true , it is absolutely paradoxical ; we cannot understand it , and we don’t know what it means . But we have proved it , and therefore we know it must be the truth (先生们，这是千真万确的，这绝对是自相矛盾的；我们无法理解它，也不知道它意味着什么。但是我们已经证明了，因此我们知道这一定是这样)。

关于Euler恒等式，

Euler恒等式可以看作是代表深刻数学美的一个方程。有五个数学量由三个基本算术运算——加法、求幂和乘法——联系起来。 更令人着迷的是它们都只发生一次。以下是使用的五个数学量：

    •  数0：在恒等式中用作加；

------------------- ---------------图15 Benjamin Peirce (1809-1880)-----------------------------------

Charles Hermite(见图 16)是一位法国数学家，他从事数的定理(number theorems)、二次型(quadratic forms)和复数几何(complex geometry)方面的研究。

 Leonhard Euler被广泛地认为是第一个证明数 e 的非比率性的数学家(如前所示)。 然而，在 1873 年，Hermite 通过证明它不是代数数(algebraic number)(即，能满足整系数代数方程的数)，成功地证明了数 e 的非比率性(irrationality)。对于任何数学家来说，笃信 e 是代数数都是荒谬的 [3]。

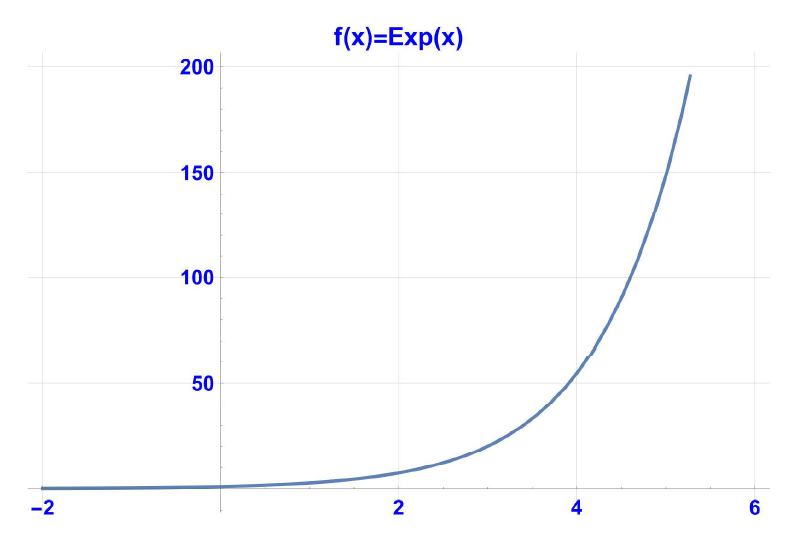
--------------------------------图16 Charles Hermite circa (1822-1901)-------------------------------------

在接下来的几年里，其他数学家致力于 e 的十进制展开。1884 年，Boorman 成功地将 e 计算到小数点后 346 位。在他的计算中，他证明了Shanks 的计算精确到小数点后 187位。

迄今为止，使用计算机程序可以将 e 的值精确到十亿位小数。就像π一样，非比率数 e 仍然让全世界的数学家着迷。它用于商业、工程和地理。非比率数确实是一个奇迹。

在这里清晰地描绘了e的美。如果方程  是图形化的，则可以求得：

(1) 曲线上任何给定点的斜率也等于 e 自乘 x ；

(2) 从负无穷大到 x 的曲线下形成的面积也从 e 自乘 x 。

函数  仅仅是迄今为止所研究的所有科学和数学领域中唯一满足上述两点的以 e 为底的函数。它使人们认识到 e 与指数增长的概念有多么密切相关(见图17)。

-------------------------------------------------图17  的草图-----------------------------------------------------

宇宙包罗万象，人类所能感知和理解的是无限的。不知道还有什么其他神秘而美丽的非比率数在哪里等待被发现。人类精神的意志是不屈不挠的，因此，如果寻求更好地理解宇宙和所有在结构上是关键的数如 e 是所期望的，那么它可以而且将会被发现和理解。

参考文献：

[1] Maor, E. (2011) e: The Story of a Number. Princeton University Press, Princeton.

[2] Agarwal, R.P., Agarwal, H. and Sen, S.K. (2013) Birth, Growth and Computation of

Pi to Ten Trillion Digits. Advances in Difference Equations , 2013, Article No. 100.

https://doi.org/10.1186/1687-1847-2013-100 [3] Breckon, M. (2016) MacTutor History of Mathematics Archive, Reference Reviews.

https://mathshistory.st-andrews.ac.uk/

[4] Arana, A. (2016) Imagination in Mathematics. Routledge, Milton Park.

[5] Reichert, S. (2019) e Is Everywhere. Nature Physics , 15, 982.

https://doi.org/10.1038/s41567-019-0655-9

[6] Müller, H. (2019) On the Cosmological Significance of Eulers Number. Progress in

Physics , 15, 17-21.

[7] Pellis, S. (2021) Unification Archimedes Constant π, Golden Ratio φ, Euler’s Number

e and Imaginary Number i, Golden Ratio φ, Euler’s Number e and Imaginary

Number i (October 10, 2021). https://doi.org/10.2139/ssrn.3975869

[8] Hollings, C.D. (2016) The History of Number Theory Birkbeck. Journal of the British

Society for the History of Mathematics , 31, 250-252.

[9] Perfileev, M.S. (2019) Combinatorial Meaning of Euler’s Number. International Research

Journal , 86, 25-28.

[10] Stojkovic, N., Grezova, K., Zlatanovska, B., Kocaleva, M., Stojanova, A. and Golubovski,

R. (2018) Eulers Number and Calculation of Compound Interest. IX International

Conference of Information Technology and Development of Education ITRO,

Zrenjanin, June 29 2018, 63-68.

内容来源：网络整理