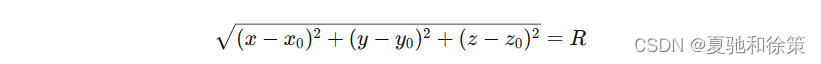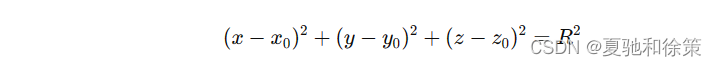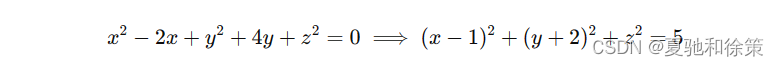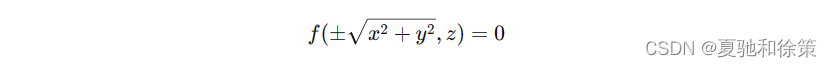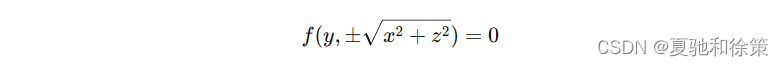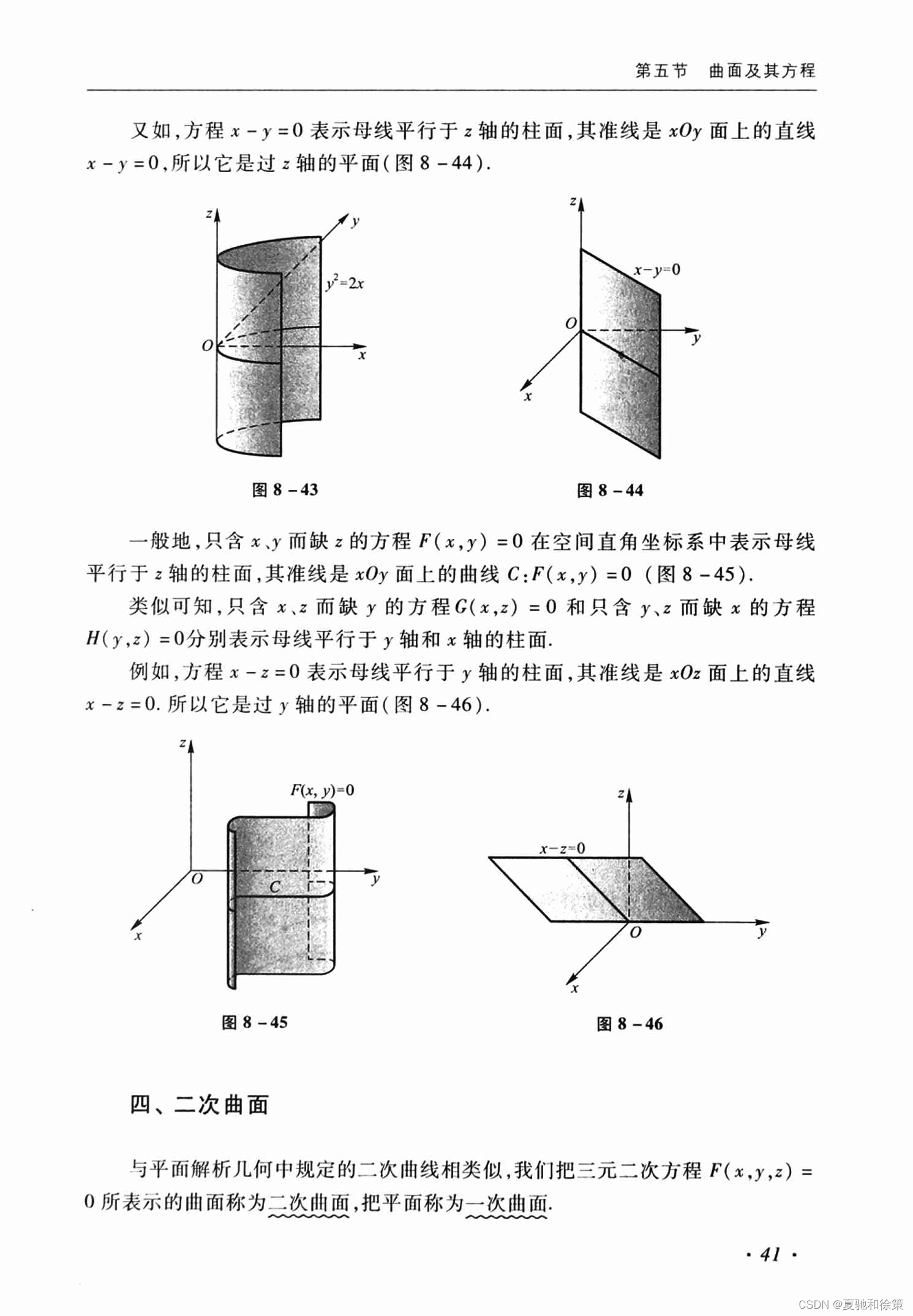
在空间解析几何中，对曲面的研究主要涉及以下两个基本问题：

已知曲面作为点的几何轨迹时，建立这曲面的方程：例如，已知一个平面的定义，可以建立相应的平面方程。这种问题通常涉及将几何知识转化为数学表达。

已知坐标 𝑥x、𝑦y 和 𝑧z 间的一个方程时，研究这方程所表示的曲面的形状：这涉及识别和描述由方程确定的几何形状。

考虑球心在点 𝑀0(𝑥0,𝑦0,𝑧0)M0​(x0​,y0​,z0​)、半径为 𝑅R 的球面。设 𝑀(𝑥,𝑦,𝑧)M(x,y,z) 是球面上的任一点，则点 𝑀M 到 𝑀0M0​ 的距离等于 𝑅R。由距离公式得：

平方后，我们得到球面的方程：

这个方程定义了一个以 𝑀0M0​ 为中心，半径为 𝑅R 的球面。

首先通过配方技巧改写原方程：

与标准球面方程 (𝑥−𝑥0)2+(𝑦−𝑦0)2+(𝑧−𝑧0)2=𝑅2(x−x0​)2+(y−y0​)2+(z−z0​)2=R2 比较，可知方程表示球心在 𝑀0(1,−2,0)M0​(1,−2,0)，半径为 55​ 的球面。

旋转曲面是由一条固定平面上的曲线（母线）绕该平面上的一条直线（轴）旋转一周生成的。

设有曲线 𝐶C 在 𝑦𝑂𝑧yOz 平面上，方程为 𝑓(𝑦,𝑧)=0f(y,z)=0。若将 𝐶C 绕 𝑧z 轴旋转，可生成一个旋转曲面。设 𝑀1(0,𝑦1,𝑧)M1​(0,y1​,z) 为曲线 𝐶C 上的一点，满足 𝑓(𝑦1,𝑧)=0f(y1​,z)=0。

当 𝑀1M1​ 绕 𝑧z 轴旋转时，𝑧z 坐标保持不变，点 𝑀1M1​ 的新位置 𝑀(𝑥,𝑦,𝑧)M(x,y,z) 满足 𝑦2+𝑥2=𝑦12y2+x2=y12​。因此，代入 𝑦1=±𝑥2+𝑦2y1​=±x2+y2​ 到 𝑓f 中，得到旋转曲面的方程：

如果曲线 𝐶C 绕 𝑦y 轴旋转，类似的方法可以得到旋转曲面的方程为：

通过这种方式，我们可以探讨各种旋转曲面的性质，从而更全面地理解它们在空间中的行为和结构。

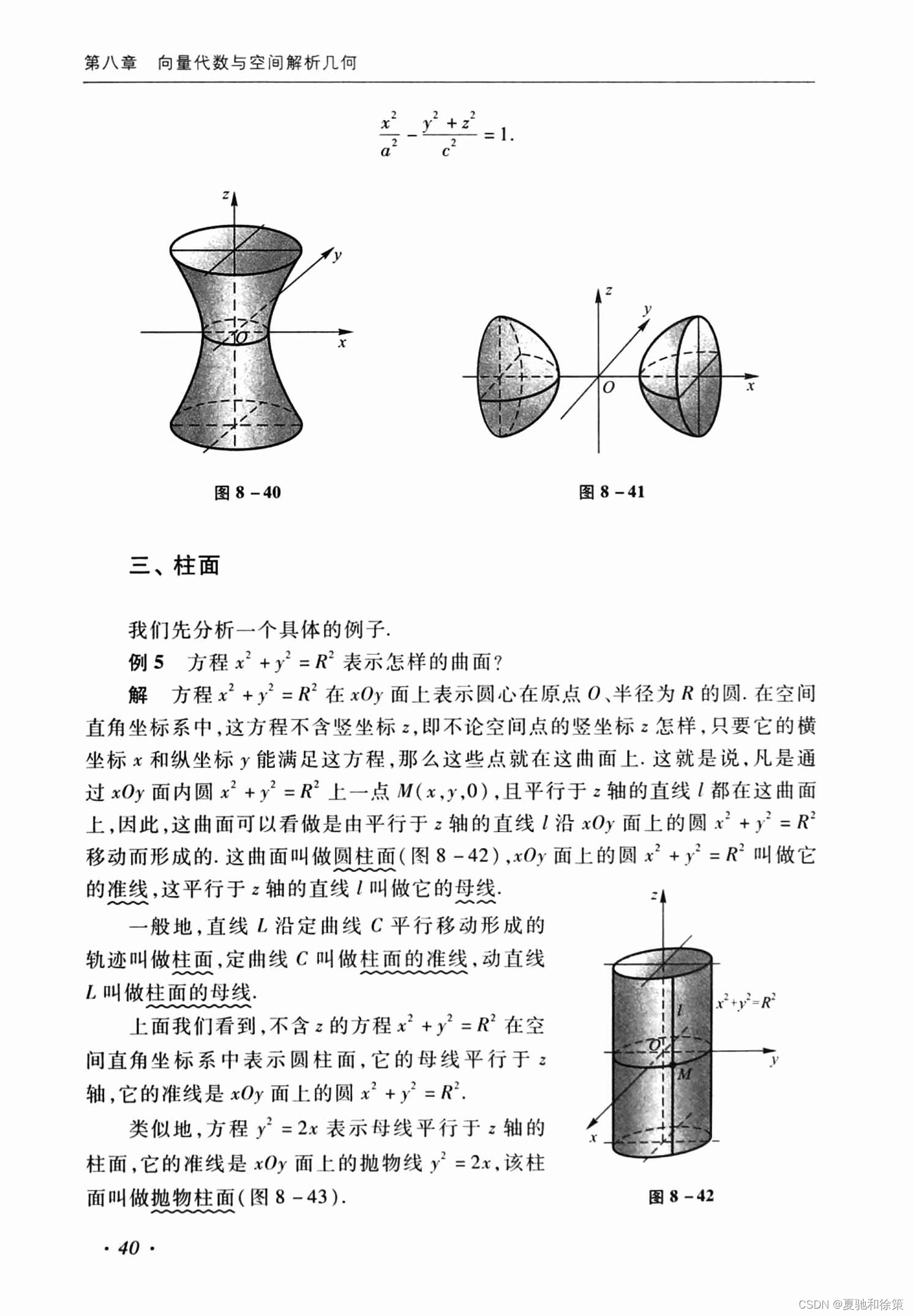
考虑在 𝑦𝑂𝑧yOz 坐标面上，直线 𝐿L 的方程为 𝑧=𝑦cot⁡𝛼z=ycotα。这是因为直线 𝐿L 与 𝑧z 轴的夹角为 𝛼α，且 cot⁡𝛼cotα 是该夹角的余切，表示 𝑧z 坐标与 𝑦y 坐标的比率。

当直线 𝐿L 绕 𝑧z 轴旋转一周时，生成的曲面是一个圆锥面。因为旋转过程中，任一点 𝑀(𝑥,𝑦,𝑧)M(x,y,z) 在 𝑧z 轴的投影保持不变，而 𝑀M 到 𝑧z 轴的距离 𝑑=𝑥2+𝑦2d=x2+y2​ 是常数。因此，将方程 𝑧=𝑦cot⁡𝛼z=ycotα 中的 𝑦y 替换为 𝑥2+𝑦2x2+y2​，得到： 𝑧=𝑥2+𝑦2cot⁡𝛼z=x2+y2​cotα

整理上述方程，得到圆锥面的标准方程： 𝑧=𝑥2+𝑦2cot⁡𝛼或𝑧2=(𝑥2+𝑦2)cot⁡2𝛼z=x2+y2​cotα或z2=(x2+y2)cot2α 这表明，圆锥面上任一点 𝑀M 的坐标满足此方程。如果点 𝑀M 不在圆锥面上，则直线 𝑂𝑀OM 与 𝑧z 轴的夹角不等于 𝛼α，从而 𝑀M 的坐标不满足上述方程。

绕 𝑧z 轴旋转： 给定双曲线 𝑦2−𝑥2=1y2−x2=1。当它绕 𝑧z 轴旋转时，生成的是一个旋转单叶双曲面。这是因为旋转过程中，任何点 (𝑥,𝑦,𝑧)(x,y,z) 到 𝑧z 轴的水平距离 𝑑=𝑥2+𝑦2d=x2+y2​ 替换 𝑦y 的值，得到： 𝑥2+𝑦2−𝑧2=1x2+y2−z2=1 这是旋转单叶双曲面的标准方程。

绕 𝑥x 轴旋转： 同样的双曲线 𝑦2−𝑧2=1y2−z2=1 绕 𝑥x 轴旋转生成的是旋转双叶双曲面。此时，任何点 (𝑥,𝑦,𝑧)(x,y,z) 到 𝑥x 轴的垂直距离 𝑑=𝑦2+𝑧2d=y2+z2​ 替换 𝑦y 的值，得到： 𝑦2+𝑧2−𝑥2=1y2+z2−x2=1 这是旋转双叶双曲面的标准方程。

这两种旋转曲面是三维空间中非常重要的几何形状，它们不仅在数学领域，也在物理和工程学中有广泛的应用。

二次曲面是通过三元二次方程 𝐹(𝑥,𝑦,𝑧)=0F(x,y,z)=0 定义的空间曲面，类似于平面解析几何中的二次曲线。它们由于方程中包含 𝑥,𝑦,𝑧x,y,z 的二次项以及可能的交叉乘积项，表现出丰富的几何形状。以下是九种基本二次曲面的讨论：

椭圆锥面的方程可以由椭圆旋转得出。若以垂直于 𝑧z 轴的平面 𝑧=𝑡z=t 截此曲面，截面为椭圆，随 𝑡t 的变化，椭圆逐渐收缩至顶点（0,0,0）。椭圆锥面的标准方程为： 𝑥2/𝑎2+𝑦2/𝑏2=𝑧2x2/a2+y2/b2=z2

椭球面是空间中一个封闭的曲面，形似拉伸或压缩的球。它可以由旋转椭圆通过沿 𝑦y 轴伸缩得到。椭球面的标准方程为： 𝑥2/𝑎2+𝑦2/𝑏2+𝑧2/𝑐2=1x2/a2+y2/b2+z2/c2=1 当 𝑎=𝑏=𝑐a=b=c 时，椭球面退化为球面。

单叶双曲面可以通过旋转双曲线 𝑦2−𝑧2=𝑎2y2−z2=a2 绕 𝑧z 轴得到，并可通过沿 𝑦y 轴的伸缩变形得到最终形状。单叶双曲面的标准方程为： 𝑥2/𝑎2+𝑦2/𝑏2−𝑧2/𝑐2=1x2/a2+y2/b2−z2/c2=1

双叶双曲面由 𝑦2−𝑧2=−𝑎2y2−z2=−a2 绕 𝑥x 轴旋转生成，具有两个分开的部分。双叶双曲面的标准方程为： 𝑥2/𝑎2−𝑦2/𝑏2−𝑧2/𝑐2=1x2/a2−y2/b2−z2/c2=1

椭圆抛物面由平面上的抛物线 𝑦2=2𝑝𝑥y2=2px 绕 𝑧z 轴旋转生成。椭圆抛物面的标准方程为： 𝑥2+𝑦2=2𝑝𝑧x2+y2=2pz

双曲抛物面，也称为马鞍面，通常由截痕法来分析。例如，平面 𝑥=𝑡x=t 截双曲抛物面可能得到一系列抛物线，其顶点在 𝑦=0y=0 平面上形成另一抛物线。双曲抛物面的标准方程为： 𝑥2/𝑎2−𝑦2/𝑏2=𝑧x2/a2−y2/b2=z

由二次曲线的直线平行移动形成，包括椭圆柱面、双曲柱面、抛物柱面等。柱面方程通常不涉及 𝑧z 坐标，例如 𝑥2/𝑎2+𝑦2/𝑏2=1x2/a2+y2/b2=1 （椭圆柱面）， 𝑥2/𝑎2−𝑦2/𝑏2=1x2/a2−y2/b2=1 （双曲柱面）， 𝑦2=4𝑝𝑥y2=4px （抛物柱面）。

二次曲面的形状和性质极大地丰富了三维空间中的几何结构，它们在物理、工程和其他科学领域中有广泛的应用，例如在光学和力学系统的设计中。