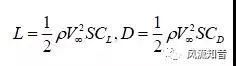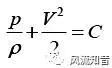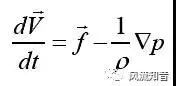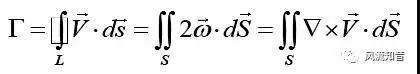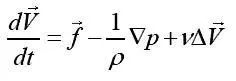飞行器的升力和阻力

众所周知，空气动力学是研究物体与空气之间存在相对运动时（物体在静止空气中的运动，或者静止物体被运动的空气绕过），物体所受的空气动力及其空气运动的规律。空气对物体的作用力在垂直于来流方向的分力体现为升力，其是使物体离开地面的作用力。而在平行于来流方向的分力体现为阻力，其对物体在空气中运动起阻力作用。

长期以来人类渴望像小鸟一样在空中自由飞翔，有许多美丽而玄妙的神话与传说都与飞行有关，譬如古希腊与古罗马的架战车飞行、羽衣飞行、丘比特飞行射箭等，中国的飞车、嫦娥奔月等。这些美妙的传说，无一不表现出人类对翱翔天空、凌云御风的遐想。但作为科学记载，最早对空气流动给出描述的应属古代先哲、古希腊科学家亚里士多德（Aristotle，公元前384年～公元前322年）。公元前350年，亚里士多德首先给出了一种描述空气的连续性模型，发现物体在连续空气中运动时会受到阻力。

亚里士多德（Aristotle，公元前384年～公元前322年）

公元前250年，古希腊科学家阿基米德（Archimedes，公元前287年—公元前212年），提出流体静力学原理（即物体在静止水体中的浮力定理），发现在水体中存在压差时，水体将发生运动。

阿基米德

（Archimedes，公元前287年—公元前212年）

经过黑暗的中世纪进入文艺复兴时期，意大利全才科学家达•芬奇（Leonardo Da Vinci，1452～1519年）通过对鸟飞行的大量观测与研究，发现在鸟翼下翼面存在高密度、高压的空气，从而使鸟翼受到向上的力（升力），认为鸟是一台按照数学法则（力平衡法则）工作的仪器，在飞行时鸟的重心与压力中心不重合，以及对空气流动和流线型物体可以减阻等给出定性描述。

达•芬奇（Leonardo Da Vinci，1452～1519年）

据记载，1673年法国物理学家马略特（Edme Mariotte,1620年～1684年）通过大量水射流对平板冲击力测量试验首次发现，机翼的升力与飞行速度的平方成正比。

马略特（Edme Mariotte,1620年～1684年）

1668年，荷兰物理学家惠更斯（Christiaan Huygens，1629年～1695年，如图5所示）在研究物体降落特性时，发现物体的阻力正比于速度的平方，而非达芬奇的一次方。

惠更斯（Christiaan Huygens，1629年～1695年）

微积分问世后，科学研究进入到定量化的时代，其中创立的连续可微函数与质点力学结合的经典连续介质力学理论，构成力学快速发展的理论基础。在1687年，英国科学家牛顿(Isaac Newton，1642年～1726年) 在其著的《自然哲学之数学原理》中首次定量给出作用于机翼的升力和阻力表达式。即

其中，L和D为升力和阻力，V∞为飞行速度，S为机翼面积，CL和CD为升力系数和阻力系数，ρ为空气的密度。

牛顿(Isaac Newton，1642年～1726年)

英国乔治•凯利（George Cayley，1773～1857年）被称为经典空气动力学之父，对鸟类飞行原理进行了大量的研究，通过对鸟翼面积、鸟的体重和飞行速度的观察，估算出速度、翼面积和升力之间的关系，发现机翼的升力除正比飞行速度的平方和机翼面积外，还随机翼的迎角发生变化。同时建议，人造飞行器应该将推进动力和升力面分开考虑。美国兰利（Langley , SamuelPierpont，1834～1906年）提出了机翼升力计算公式。

英国乔治•凯利（George Cayley，1773～1857年）

兰利（Langley , SamuelPierpont，1834～1906年）

德国工程师和滑翔飞行家李林达尔（Otto Lilienthal，1848～1896年，如图9所示）开始制造滑翔机，他是制造与实践固定翼滑翔机的航空先驱者之一，并在柏林附近试飞2000多次，积累了丰富的资料，为日后美国莱特兄弟实现动力飞行提供了宝贵的经验。

李林达尔（Otto Lilienthal，1848～1896年）

英国空气动力学家兰彻斯特（F. W. Lanchester，1868～1946年），在1891年的论文中指出重于空气飞行器的飞行原理，发现了机翼的翼尖涡（如图11所示），1894年首先解释了机翼产生升力原理，提出了正确的计算方法。

兰彻斯特（F. W. Lanchester，1868～1946年）

兰彻斯特给出的机翼翼梢涡

美国莱特兄弟是两个既有实践经验又有理论知识，且富有想象力和远见的工程师（威尔伯•莱特，Wilbur Wright，1867～1912年；奥维尔•莱特，Orville Wright，1871～1948年），在1903年12月27日，奥维尔•莱特驾驶他们设计制造“飞行者一号”首次试飞成功，这是人类历史上第一架有动力、载人、持续、稳定、可操纵的飞行器。从此开创了动力飞行的新纪元。其后，飞机的发展推动了空气动力学的迅速发展。

左：威尔伯•莱特（Wilbur Wright，1867～1912年）

右：奥维尔•莱特（Orville Wright，1871～1948年）

升力与环量定律

当17世纪后期，英国科学家牛顿和德国科学家莱布尼茨（Gottfried Wilhelm Leibniz，1646～1716年）发明微积分后，数学和力学家们很快将微积分连续可微函数与质点力学理论结合起来，建立了经典连续介质力学，这为流体力学和空气动力学的发展奠定了坚实的理论基础。

莱布尼茨

（Gottfried Wilhelm Leibniz，1646～1716年）

1738 年瑞士科学家伯努利（Daniel Bernoulli，1700年～1782年）将质点的动能定理用于同一理想流体微元流管上，导出了一元流机械能守恒方程，即著名的理想流体定常流动能量方程(后称为伯努利方程)。对于理想不可压缩流体的定常流动，在不计质量力的情况下，伯努利方程表明，沿同一条流线上单位质量流体质点的压强势能和动能之和为常数。

伯努利（Daniel Bernoulli，1700年～1782年）

伯努利方程的发现，正确地回答了机翼上翼面吸力对升力的贡献缘由。后来的风洞试验表明：对于翼型而言，上翼面吸力的贡献约占翼型总升力的60%～70%。1755年瑞士数学家与流体力学家欧拉（Leonhard Euler , 1707年～1783年），提出描述流体运动的欧拉方法，并基于连续介质假设和理想流体模型，利用牛顿第二定理建立了理想流体运动微分方程组，即欧拉方程组。

欧拉（Leonhard Euler , 1707年～1783年）

对于质量力有势、理想不可压缩流体的定常流动，沿着流线积分欧拉方程组，可得到伯努利方程。进一步研究表明，不仅沿着同一条流线满足伯努利方程，沿着同一条涡线、势流流场、螺旋流均满足伯努利方程。

进入19世纪，流体力学重点发展了理想流体无旋运动的求解，建立了理想流体旋涡运动理论和粘性流体运动微分方程组等。 1858年德国流体力学家亥姆霍茲（Hermann Ludwig Ferdinand von Helmholtz，1821～1894年），提出流体质团的速度分解定理，同时研究了理想不可压缩流体在有势力作用下的有旋运动，提出亥姆霍茲旋涡运动的三大定律，即沿涡管的涡强不变定律、涡管保持定律和涡强守恒定律，建立了理想流体旋涡运动理论。在流场中任取一条封闭曲线，速度沿该封闭曲线的线积分称为该封闭曲线的速度环量，速度环量的符号不仅决定于流场的速度方向，而且与封闭曲线的绕行方向有关，规定积分时逆时针绕行方向为正。根据Stokes线积分与面积分公式，在速度矢量场中，沿任意封闭曲线的速度环量等于该封闭曲线所张的任意曲面的涡通量。即

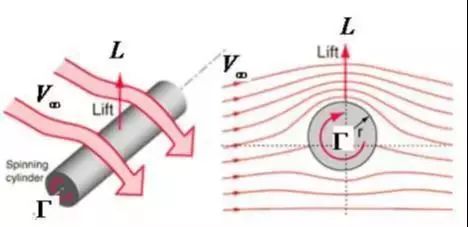
亥姆霍茲（Hermann Ludwig Ferdinand von Helmholtz，1821～1894年）

为了确定翼型的升力，1902年德国数学家库塔（Martin Wihelm Kutta，1867～1944年)和1906年俄国物理学家儒可夫斯基（N. Joukowski，1847～1921年），将有环量圆柱绕流升力计算公式推广到任意形状物体的绕流，提出对于任意形状物体的绕流，只要存在速度环量，就会产生升力，升力方向沿着来流方向按反环量旋转90°，后人称为库塔、儒可夫斯基升力环量定律。即

式中，L为作用在绕流物体上的升力，ρ为来流空气密度，V∞为来流速度，Γ为绕流物体的速度环量。

儒可夫斯基升力环量定律

库塔（Martin Wihelm Kutta，1867～1944年)

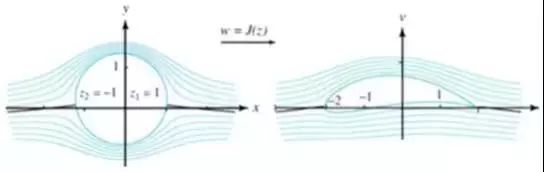
儒可夫斯基（N. Joukowski，1847～1921年）

1909年儒可夫斯基利用复变函数的保角变换法研究了理想流体翼型定常绕流，提出著名的儒可夫斯基翼型理论。

儒可夫斯基翼型

在第一次世界大战期间，交战各国都在实践中摸索出一些性能较好的翼型。如儒可夫斯基翼型、德国Gottingen翼型，英国的RAF 翼型（Royal Air Force英国空军；后改为RAE翼型～Royal Aircraft Estabilishment 皇家飞机研究院）， 美国的Clark～Y等。

20世纪30年代以后，出现美国NACA翼型（NationalAdvisory Committee for Aeronautics，后来为 NASA，NationalAeronautics and Space Administration）和前苏联的ЦА Γ И 翼型（中央空气流体研究院）。美国国家航空咨询委员会（缩写为 NACA，现在NASA）在20世纪30年代后期，对翼型的性能作了系统的研究，提出了NACA四位数翼族和五位数翼族等。

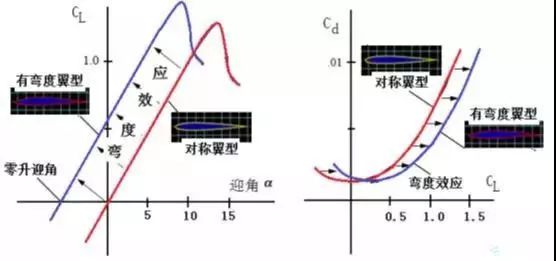
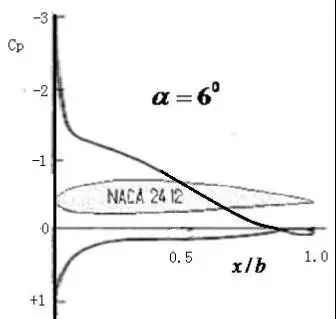
翼型的升力系数与阻力系数

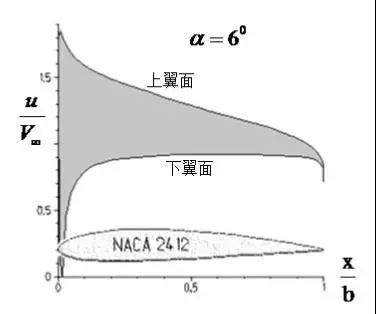
NACA2412翼型上下翼面上的速度和压强分布

与此同时，鉴于理想流体圆柱绕流无阻力结论与实际不符，人们开始研究粘性流体运动，经1822年法国工程师纳维（Claude-Louis Navier，1785〜1836年）开始，最后由1845年英国科学家斯托克斯（GeorgeGabriel Stokes，1819～1903年）在剑桥大学三一学院完成了牛顿流体运动微分方程组，即著名的纳维-斯托克斯（Navier-Stokes）方程组，简称N-S方程组。对于不可压缩粘性流体运动的微分方程组，其矢量形式为

这个方程组说明，导致流体微团加速度变化的是作用于流体微团上的质量力、压强差力（表面法向力）和粘性力。

纳维（Claude-Louis Navier，1785〜1836年）

斯托克斯（GeorgeGabriel Stokes，1819～1903年）

1904 年世界流体力学大师德国力学家普朗特（Ludwig Prandtl，1875～1953年），在德国海德尔堡第三次国际数学年会上发表了一篇论小粘性流体运动的论文，提出著名的边界层概念，深刻阐述了绕流物体在大雷诺数情况下表面受粘性影响的边界层流动特征及其控制方程，巧妙地解决了整体流动和局部流动的关系问题，从而为解决粘性流体绕过物体的阻力问题找到了新的途径，起到划时代的里程碑作用。

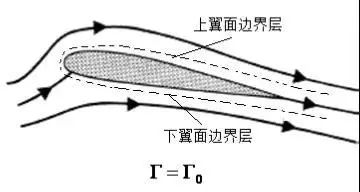
翼型绕流边界层发展

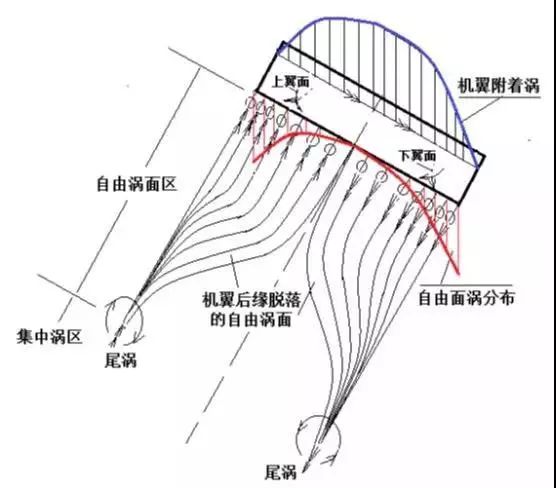
普朗特（Ludwig Prandtl，1875～1953年）

在1911年至1918年，普朗特通过风洞试验发现，大展弦比的直机翼（机翼前缘后掠角小于20度，展弦比大于5）绕流，因受展向流动的影响，绕过机翼的流动可用直匀流叠加附着涡（线）和自由涡面的模型取代，附着涡和自由涡面之间用无数条Π形马蹄涡联系，称为升力面模型。

大展弦比直机翼附着涡与自由涡关系

该气动模型只所以符合实际绕流，原因如下：（1）该模型符合沿一根涡线强度不变，且不能在流体中中断的理想流体涡强不变定理；（2）Π形马蹄涡垂直来流的部分是附着涡，可代替机翼的升力作用，展向各剖面上通过的涡线数目不同，附着涡强也不同。其中，中间剖面通过的涡线最多，环量最大；翼端剖面无涡线通过，环量为零，模拟了环量和升力的展向分布（椭圆分布最佳）。由此可见，附着涡的强度沿展向是变化的，与剖面升力分布相同，在翼梢处为零，在翼根处最大；（3）Π形马蹄涡系平行来流且拖向下游无限远，模拟了自由涡面。由于展向相邻两剖面间拖出的自由涡强度等于这两个剖面上附着涡的环量差，从而建立了展向自由涡线强度与机翼上附着涡强之间的关系；（4）对大展弦比直机翼，由于弦长比展长小得多，因此可以近似将机翼上的附着涡系合并成一条展向变强度的附着涡线，各剖面的升力就作用在该线上，称其升力线假设。因为低速翼型的升力增量在焦点处，约在1/4弦点，因此附着涡线可放在展向各剖面的1/4弦点的连线上，此线即为升力线。升力线理论是求解大展弦比直机翼的近似势流理论。可在知道机翼平面形状和翼型气动数据后，就能够求出环量分布、剖面升力系数分布及整个机翼的升力系数、升力线斜率以及诱导阻力系数。其突出的优点是可以明确地给出机翼平面参数对机翼气动特性的影响。

致谢及声明：

本文转载自“风流知音”公众号，其他公众号转载请联系“风流知音”公众号授权，读者转发朋友圈请随意。诚挚感谢刘沛清教授、杨小权副教授、徐胜金副教授对分会科普工作的支持！

2019汽车空气动力学分会青年精英学术沙龙

启动报名，会员免费参加！

分会 | “2019汽车空气动力学分会青年精英学术沙龙——长春站”欢迎您！

通

知

2019汽车空气动力学分会学术年会征文进行中！

3月20日提交论文摘要！

中国汽车工程学会汽车空气动力学分会将于2019年9月4-6日在重庆举办2019汽车空气动力学分会学术年会。本届年会将围绕汽车空气动力学、汽车热管理、汽车气动噪声等相关技术领域进行研讨，交流形式包括：特邀专家主会场报告、优秀论文专题分会场宣讲、C-STAA技术发布会、创新发展专题论坛、专业技术培训、先进技术成果展示等。

2019汽车空气动力学分会学术年会现面向行业科技工作者征集学术论文（或扩展摘要）。投稿论文经学术委员会专家评审录用后将刊登在会议论文集上；优秀论文将安排专题分会场宣讲并参与论文现场评奖；获奖论文将由中国汽车工程学会颁发相应的证书；部分优秀论文将被核心期刊收录。

分会 | 2019汽车空气动力学分会学术年会征文通知（第一轮）

参加汽车空气动力学分会“原创之星”活动

赢取2019年会免费入场券

“汽车空气动力学分会微信公众号原创之星”等你来摘！

END返回搜狐，查看更多