算法数据结构

#算法数据结构| 来源: 网络整理| 查看: 265

1. 拓扑排序简介

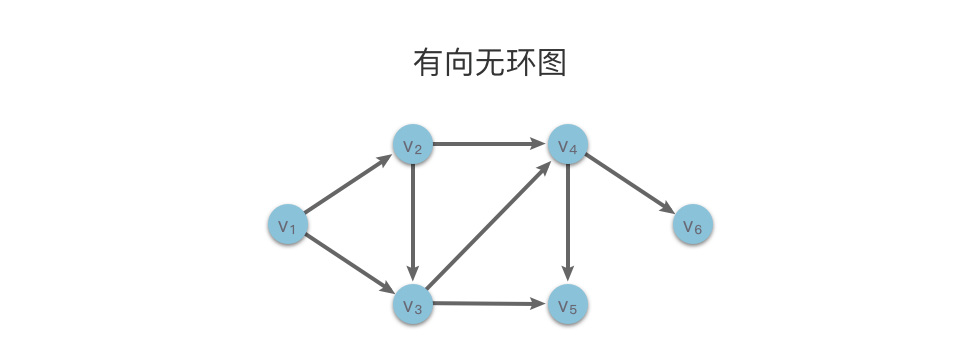
拓扑排序（Topological Sorting）：一种对有向无环图（DAG）的所有顶点进行线性排序的方法，使得图中任意一点 $u$ 和 $v$，如果存在有向边 $$，则 $u$ 必须在 $v$ 之前出现。对有向图进行拓扑排序产生的线性序列称为满足拓扑次序的序列，简称拓扑排序。

图的拓扑排序是针对有向无环图（DAG）来说的，无向图和有向有环图没有拓扑排序，或者说不存在拓扑排序。

如上图中的有向无环图（DAG）所示，$v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4 \rightarrow v_5 \rightarrow v_6$ 是该图的一个拓扑序列。与此同时，$v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4 \rightarrow v_6 \rightarrow v_5$ 也是该图的一个拓扑序列。也就是说，对于一个有向无环图来说，拓扑序列可能不止一个。

2. 拓扑排序的实现方法

拓扑排序有两种实现方法，分别是「Kahn 算法」和「DFS 深度优先搜索算法」。接下来我们依次来看下它们是如何实现的。

2.1 Kahn 算法

Kahn 算法的基本思想：

不断找寻有向图中入度为 $0$ 的顶点，将其输出。

然后删除入度为 $0$ 的顶点和从该顶点出发的有向边。

重复上述操作直到图为空，或者找不到入度为 $0$ 的节点为止。

2.1.1 Kahn 算法的实现步骤

使用数组 $indegrees$ 用于记录图中各个顶点的入度。

维护一个入度为 $0$ 的顶点集合 $S$（可使用栈、队列、优先队列）。

每次从集合中选择任何一个没有前驱（即入度为 $0$）的顶点 $u$，将其输出到拓扑序列 $order$ 中。

从图中删除该顶点 $u$，并且删除从该顶点出发的有向边 $$（也就是把该顶点可达的顶点入度都减 $1$）。如果删除该边后顶点 $v$ 的入度变为 $0$，则将顶点 $v$ 放入集合 $S$ 中。

重复上述过程，直到集合 $S$ 为空，或者图中还有顶点未被访问（说明一定存在环路，无法形成拓扑序列）。

如果不存在环路，则 $order$ 中顶点的顺序就是拓扑排序的结果。

2.1.2 Kahn 算法的实现代码

import collections class Solution: # 拓扑排序，graph 中包含所有顶点的有向边关系（包括无边顶点） def topologicalSortingKahn(self, graph: dict): indegrees = {u: 0 for u in graph} # indegrees 用于记录所有顶点入度 for u in graph: for v in graph[u]: indegrees[v] += 1 # 统计所有顶点入度 # 将入度为 0 的顶点存入集合 S 中 S = collections.deque([u for u in indegrees if indegrees[u] == 0]) order = [] # order 用于存储拓扑序列 while S: u = S.pop() # 从集合中选择一个没有前驱的顶点 0 order.append(u) # 将其输出到拓扑序列 order 中 for v in graph[u]: # 遍历顶点 u 的邻接顶点 v indegrees[v] -= 1 # 删除从顶点 u 出发的有向边 if indegrees[v] == 0: # 如果删除该边后顶点 v 的入度变为 0 S.append(v) # 将其放入集合 S 中 if len(indegrees) != len(order): # 还有顶点未遍历（存在环），无法构成拓扑序列 return [] return order # 返回拓扑序列 def findOrder(self, n: int, edges): # 构建图 graph = dict() for i in range(n): graph[i] = [] for u, v in edges: graph[u].append(v) return self.topologicalSortingKahn(graph) 2.2 基于 DFS 实现拓扑排序算法

基于 DFS 实现拓扑排序算法的基本思想：

对于一个顶点 $u$，深度优先遍历从该顶点出发的有向边 $$。如果从该顶点 $u$ 出发的所有相邻顶点 $v$ 都已经搜索完毕，则回溯到顶点 $u$ 时，该顶点 $u$ 应该位于其所有相邻顶点 $v$ 的前面（拓扑序列中）。

这样一来，当我们对每个顶点进行深度优先搜索，在回溯到该顶点时将其放入栈中，则最终从栈顶到栈底的序列就是一种拓扑排序。

2.2.1 基于 DFS 实现拓扑排序算法实现步骤

使用集合 $visited$ 用于记录当前顶点是否被访问过，避免重复访问。

使用集合 $onStack$ 用于记录同一次深度优先搜索时，当前顶点是否被访问过。如果当前顶点被访问过，则说明图中存在环路，无法构成拓扑序列。

使用布尔变量 $hasCycle$ 用于判断图中是否存在环。

从任意一个未被访问的顶点 $u$ 出发。

如果顶点 $u$ 在同一次深度优先搜索时被访问过，则说明存在环。

如果当前顶点被访问或者有环时，则无需再继续遍历，直接返回。

将顶点 $u$ 标记为被访问过，并在本次深度优先搜索中标记为访问过。然后深度优先遍历从顶点 $u$ 出发的有向边 $$。

当顶点 $u$ 的所有相邻顶点 $v$ 都被访问后，回溯前记录当前节点 $u$（将当前节点 $u$ 输出到拓扑序列 $order$ 中）。

取消本次深度优先搜索时，顶点 $u$ 的访问标记。

对其他未被访问的顶点重复 $4 \sim 7$ 步过程，直到所有节点都遍历完，或者出现环。

如果不存在环路，则将 $order$ 逆序排序后，顶点的顺序就是拓扑排序的结果。

2.2.2 DFS 深度优先搜索算法实现代码

import collections class Solution: # 拓扑排序，graph 中包含所有顶点的有向边关系（包括无边顶点） def topologicalSortingDFS(self, graph: dict): visited = set() # 记录当前顶点是否被访问过 onStack = set() # 记录同一次深搜时，当前顶点是否被访问过 order = [] # 用于存储拓扑序列 hasCycle = False # 用于判断是否存在环 def dfs(u): nonlocal hasCycle if u in onStack: # 同一次深度优先搜索时，当前顶点被访问过，说明存在环 hasCycle = True if u in visited or hasCycle: # 当前节点被访问或者有环时直接返回 return visited.add(u) # 标记节点被访问 onStack.add(u) # 标记本次深搜时，当前顶点被访问 for v in graph[u]: # 遍历顶点 u 的邻接顶点 v dfs(v) # 递归访问节点 v order.append(u) # 后序遍历顺序访问节点 u onStack.remove(u) # 取消本次深搜时的顶点访问标记 for u in graph: if u not in visited: dfs(u) # 递归遍历未访问节点 u if hasCycle: # 判断是否存在环 return [] # 存在环，无法构成拓扑序列 order.reverse() # 将后序遍历转为拓扑排序顺序 return order # 返回拓扑序列 def findOrder(self, n: int, edges): # 构建图 graph = dict() for i in range(n): graph[i] = [] for v, u in edges: graph[u].append(v) return self.topologicalSortingDFS(graph) 3. 拓扑排序的应用

拓扑排序可以用来解决一些依赖关系的问题，比如项目的执行顺序，课程的选修顺序等。

3.1 课程表 II

3.1.1 题目链接

210. 课程表 II - 力扣

3.1.2 题目大意

描述：给定一个整数 $numCourses$，代表这学期必须选修的课程数量，课程编号为 $0 \sim numCourses - 1$。再给定一个数组 $prerequisites$ 表示先修课程关系，其中 $prerequisites[i] = [ai, bi]$ 表示如果要学习课程 $ai$ 则必须要先完成课程 $bi$。

要求：返回学完所有课程所安排的学习顺序。如果有多个正确的顺序，只要返回其中一种即可。如果无法完成所有课程，则返回空数组。

说明：

$1 \le numCourses \le 2000$。

$0 \le prerequisites.length \le numCourses \times (numCourses - 1)$。

$prerequisites[i].length == 2$。

$0 \le ai, bi < numCourses$。

$ai \ne bi$。

所有$[ai, bi]$ 互不相同。

示例：

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]] 输出：[0,1] 解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1]。

示例 2：

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]] 输出：[0,2,1,3] 解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3]。

3.1.3 解题思路

思路 1：拓扑排序

这道题是「0207. 课程表」的升级版，只需要在上一题的基础上增加一个答案数组 $order$ 即可。

使用哈希表 $graph$ 存放课程关系图，并统计每门课程节点的入度，存入入度列表 $indegrees$。

借助队列 $S$，将所有入度为 $0$ 的节点入队。

从队列中选择一个节点 $u$，并将其加入到答案数组 $order$ 中。

从图中删除该顶点 $u$，并且删除从该顶点出发的有向边 $$（也就是把该顶点可达的顶点入度都减 $1$）。如果删除该边后顶点 $v$ 的入度变为 $0$，则将其加入队列 $S$ 中。

重复上述步骤 $3 \sim 4$，直到队列中没有节点。

最后判断总的顶点数和拓扑序列中的顶点数是否相等，如果相等，则返回答案数组 $order$，否则，返回空数组。

思路 1：代码

import collections class Solution: # 拓扑排序，graph 中包含所有顶点的有向边关系（包括无边顶点） def topologicalSortingKahn(self, graph: dict): indegrees = {u: 0 for u in graph} # indegrees 用于记录所有顶点入度 for u in graph: for v in graph[u]: indegrees[v] += 1 # 统计所有顶点入度 # 将入度为 0 的顶点存入集合 S 中 S = collections.deque([u for u in indegrees if indegrees[u] == 0]) order = [] # order 用于存储拓扑序列 while S: u = S.pop() # 从集合中选择一个没有前驱的顶点 0 order.append(u) # 将其输出到拓扑序列 order 中 for v in graph[u]: # 遍历顶点 u 的邻接顶点 v indegrees[v] -= 1 # 删除从顶点 u 出发的有向边 if indegrees[v] == 0: # 如果删除该边后顶点 v 的入度变为 0 S.append(v) # 将其放入集合 S 中 if len(indegrees) != len(order): # 还有顶点未遍历（存在环），无法构成拓扑序列 return [] return order # 返回拓扑序列 def findOrder(self, numCourses: int, prerequisites): graph = dict() for i in range(numCourses): graph[i] = [] for v, u in prerequisites: graph[u].append(v) return self.topologicalSortingKahn(graph)

思路 1：复杂度分析

时间复杂度：$O(n + m)$，其中 $n$ 为课程数，$m$ 为先修课程的要求数。

空间复杂度：$O(n + m)$。

3.2 找到最终的安全状态

3.2.1 题目链接

802. 找到最终的安全状态 - 力扣

3.2.2 题目大意

描述：给定一个有向图 $graph$，其中 $graph[i]$ 是与节点 $i$ 相邻的节点列表，意味着从节点 $i$ 到节点 $graph[i]$ 中的每个节点都有一条有向边。

要求：找出图中所有的安全节点，将其存入数组作为答案返回，答案数组中的元素应当按升序排列。

说明：

终端节点：如果一个节点没有连出的有向边，则它是终端节点。或者说，如果没有出边，则节点为终端节点。

安全节点：如果从该节点开始的所有可能路径都通向终端节点，则该节点为安全节点。

$n == graph.length$。

$1 \le n \le 10^4$。

$0 \le graph[i].length \le n$。

$0 \le graphi \le n - 1$。

$graph[i]$ 按严格递增顺序排列。

图中可能包含自环。

图中边的数目在范围 $[1, 4 \times 10^4]$ 内。

示例：

示例 1：

输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]] 输出：[2,4,5,6] 解释：示意图如上。节点 5 和节点 6 是终端节点，因为它们都没有出边。从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6。

示例 2：

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] 输出：[4] 解释: 只有节点 4 是终端节点，从节点 4 开始的所有路径都通向节点 4。

3.2.3 解题思路

思路 1：拓扑排序

根据题意可知，安全节点所对应的终点，一定是出度为 $0$ 的节点。而安全节点一定能在有限步内到达终点，则说明安全节点一定不在「环」内。

我们可以利用拓扑排序来判断顶点是否在环中。

为了找出安全节点，可以采取逆序建图的方式，将所有边进行反向。这样出度为 $0$ 的终点就变为了入度为 $0$ 的点。

然后通过拓扑排序不断移除入度为 $0$ 的点之后，如果不在「环」中的点，最后入度一定为 $0$，这些点也就是安全节点。而在「环」中的点，最后入度一定不为 $0$。

最后将所有安全的起始节点存入数组作为答案返回。

思路 1：代码

class Solution: # 拓扑排序，graph 中包含所有顶点的有向边关系（包括无边顶点） def topologicalSortingKahn(self, graph: dict): indegrees = {u: 0 for u in graph} # indegrees 用于记录所有节点入度 for u in graph: for v in graph[u]: indegrees[v] += 1 # 统计所有节点入度 # 将入度为 0 的顶点存入集合 S 中 S = collections.deque([u for u in indegrees if indegrees[u] == 0]) while S: u = S.pop() # 从集合中选择一个没有前驱的顶点 0 for v in graph[u]: # 遍历顶点 u 的邻接顶点 v indegrees[v] -= 1 # 删除从顶点 u 出发的有向边 if indegrees[v] == 0: # 如果删除该边后顶点 v 的入度变为 0 S.append(v) # 将其放入集合 S 中 res = [] for u in indegrees: if indegrees[u] == 0: res.append(u) return res def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]: graph_dict = {u: [] for u in range(len(graph))} for u in range(len(graph)): for v in graph[u]: graph_dict[v].append(u) # 逆序建图 return self.topologicalSortingKahn(graph_dict)

思路 1：复杂度分析

时间复杂度：$O(n + m)$，其中 $n$ 是图中节点数目，$m$ 是图中边数目。

空间复杂度：$O(n + m)$。

【本文地址】

算法数据结构

算法数据结构

今日新闻

推荐新闻