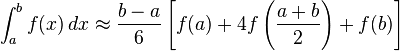辛普森积分入门讲解 |
您所在的位置:网站首页 › 函数近似计算公式是什么 › 辛普森积分入门讲解 |
辛普森积分入门讲解
|
辛普森积分
引用部分
百度一下 文库 定义辛普森积分法就是在积分区间[a,b]上去找三个点a、b和m=(a+b)/2,计算其原函数的在此处的值,然后用抛物线来拟合原函数。 正文 Simpson积分公式
用途:来求一个函数的积分的近似值,用于面积计算等精度要求不是特别苛刻的地方。 其实它就是用一个二次函数曲线不断拟合逼近原函数,然后求得原函数的近似值。 公式说明:前置: g(x) g ( x ) 为一个关于 x x 的二次函数(抛物线),其中g(x)=A×x2+B×x+Cg(x)=A×x2+B×x+C,对于求定积分 ∫x0g(x)dx ∫ 0 x g ( x ) d x ,通过求积得其等于 A×x33+B×x22+C×x+D A × x 3 3 + B × x 2 2 + C × x + D 其中 D D 为常数,可以看做00。令 W(x)=∫x0g(x)dx W ( x ) = ∫ 0 x g ( x ) d x ,所以对于求一段定积分则有 ∫bag(x)=W(b)−W(a) ∫ a b g ( x ) = W ( b ) − W ( a ) 。 在平面直角坐标系里,由 (x1,y1),(x2,y2),(x3,y3) ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (其中 x3=x1+x22 x 3 = x 1 + x 2 2 )确定的抛物线 f(x) f ( x ) 在区间[x1,x2]的定积分为: ∫x2x1f(x)dx=16×(x2−x1)×(y1+y2+4×y3) ∫ x 1 x 2 f ( x ) d x = 1 6 × ( x 2 − x 1 ) × ( y 1 + y 2 + 4 × y 3 )下面给出简单的证明: 令 g(x)=A×x2+B×x+C g ( x ) = A × x 2 + B × x + C 为拟合后的抛物线,则有 ∫x2x1f(x)dx≈∫x2x1g(x)dx ∫ x 1 x 2 f ( x ) d x ≈ ∫ x 1 x 2 g ( x ) d x =W(x2)−W(x1) = W ( x 2 ) − W ( x 1 ) =A3×(x2)3+B2×(x2)2+C×x2−(A3×(x1)3+B2×(x1)2+C×x1) = A 3 × ( x 2 ) 3 + B 2 × ( x 2 ) 2 + C × x 2 − ( A 3 × ( x 1 ) 3 + B 2 × ( x 1 ) 2 + C × x 1 ) =A3×((x2)3−(x1)3)+B2×((x2)2−(x1)2)+C×(x2−x1) = A 3 × ( ( x 2 ) 3 − ( x 1 ) 3 ) + B 2 × ( ( x 2 ) 2 − ( x 1 ) 2 ) + C × ( x 2 − x 1 ) =x2−x16×(2×A×((x2)2+x1×x2+(x1)2)+3×B×(x2+x1)+6×C) = x 2 − x 1 6 × ( 2 × A × ( ( x 2 ) 2 + x 1 × x 2 + ( x 1 ) 2 ) + 3 × B × ( x 2 + x 1 ) + 6 × C ) 展开化简整理得: =x2−x16×(A×(x1)2+B×x1+C+A×(x2)2+B×x2+C+4×A×(x2+x12)2) = x 2 − x 1 6 × ( A × ( x 1 ) 2 + B × x 1 + C + A × ( x 2 ) 2 + B × x 2 + C + 4 × A × ( x 2 + x 1 2 ) 2 ) 将其组合成完全平方式(配方)后 =x2−x16×(g(x1)+g(x2)+4×g(x1+x22)) = x 2 − x 1 6 × ( g ( x 1 ) + g ( x 2 ) + 4 × g ( x 1 + x 2 2 ) ) =x2−x16×(g(x1)+g(x2)+4×g(x3)) = x 2 − x 1 6 × ( g ( x 1 ) + g ( x 2 ) + 4 × g ( x 3 ) ) 于是我们就得到了simpson积分公式 ∫baf(x)dx≈b−a6×[g(a)+4×g(a+b2)+g(b)] ∫ a b f ( x ) d x ≈ b − a 6 × [ g ( a ) + 4 × g ( a + b 2 ) + g ( b ) ]在实际计算中 g(x) g ( x ) 的值可以用原函数 f(x) f ( x ) 的值来代替,于是就是如下公式: ∫baf(x)dx≈b−a6×[f(a)+4×f(a+b2)+f(b)] ∫ a b f ( x ) d x ≈ b − a 6 × [ f ( a ) + 4 × f ( a + b 2 ) + f ( b ) ]代码: double simpson(double l,double r){ return (r-l)*(f(l)+4*f((l+r)/2)+f(r))/6; } 自适应辛普森积分法 那么实际程序该如何实现辛普森积分求积呢?我们如果要求 ∫baf(x)dx ∫ a b f ( x ) d x 的近似值的话,可以用递归二分区间求解来达到要求精度。 用如下公式: ∫baf(x)dx=∫midaf(x)dx+∫bmidf(x)dx ∫ a b f ( x ) d x = ∫ a m i d f ( x ) d x + ∫ m i d b f ( x ) d x 其中 mid=a+b2 m i d = a + b 2 ,证明:显然式证明 :)但是因为是浮点数(小数),那么递归多少层,在什么时候返回值结束递归呢? 我们容易知道如果递归到 b−aa |
【本文地址】