【最优化】最优化理论的基本概念 |
您所在的位置:网站首页 › 函数的定义及定理解释视频讲解 › 【最优化】最优化理论的基本概念 |
【最优化】最优化理论的基本概念
|
最优化理论的基本概念
一. 最优化理论的定义与分类
1. 一般形式
(1)公式定义: m i n f ( x ) , 且 有 x ∈ X min f(x),且有 x∈X minf(x),且有x∈X 其中,对于上式中的字母,含义如下: f(x):代价函数(目标函数)x:决策向量(单值或者是向量)X:约束集合,约束集合一定是从属于n维实数空间(Rn)中的某个子空间(2)简单分类: 当X是Rn空间的真子集时,上文描述的问题就称为约束优化问题 形如下式中的问题就是约束优化问题 m i n ( x 2 ) 【 s . t . x + 1 ≤ 0 】 min (x^2) 【s.t. x+1≤0】 min(x2)【s.t.x+1≤0】 当X就是Rn空间时,上文描述的问题称为无约束优化问题 形如下式中的问题就是无约束优化问题 m i n ( x 2 ) 【 x ∈ R 】 min (x^2) 【x∈R】 min(x2)【x∈R】 (3)说明 虽然在定义中,问题被统一定义成最小化的求解形式;其实最小化和最大化之间是可以相互转化的。 Maximize f(x) ↔ Minimize -f(x) 【例】根据给出的实际题目,写出其相应的最优化形式 前面我们只是根据有没有约束条件,对优化问题进行有约束/无约束的简略分类; 在实际中,最优化问题还有别的分类依据,其中线性规划【Linear Programming】就是一种。 (1)定义 目标函数是线性的+约束条件也是线性的 → 最优化问题是线性规划问题 (2)一般形式 M i n i m i z e f ( x ) ≡ c T ⋅ x , 且 有 x ∈ X Minimize f(x)≡c^T·x,且有x∈X Minimizef(x)≡cT⋅x,且有x∈X 其中对于定义中的相关参数,作出以下规定: 约束集合X = {x∈Rn,Ax = b,x≥0}其中Ax = b,表示该线性约束是等式约束;也可以约束为Ax≤b的形式 因为是线性的表述,上式中的符号统统采用向量和矩阵的形式:c∈Rn,b∈Rm,A∈Rmxn(3)NLP(NonLinear Programming) 当目标函数是非线性的,或者限制条件是非线性的时候该最优化问题就属于非线性规划问题。 我们这门课大部分讨论的都还是非线性规划的问题,因为现实生活中的条件复杂,很难满足线性性。 3. 其他类型的优化问题(1)整数规划(Interger Programming) 也称离散优化(Discrete Optimization),要求问题定义与求解中的所有决策变量或向量都是离散的整数类型。 (2)混合整数规划(Mixed Integer Programming) 决策变量有些是整型,有些是连续型的。 (3)动态规划/最优控制(Dynamic Optimization) 需要考虑系统的动态性,往往会考虑时间的影响。 (4)随机优化(Stochastic Optimization) 需要考虑问题中的不确定性因素,比如涉及到的部分变量是随机变量,而非确定性的。 e.g. 前台接待系统中某一时段的客流量就是随机、不确定的。 (5)多目标最优化(Multi-Objective Optimization) 在进行优化时,有多个目标函数需要同时达到最优。 e.g. 比如建造房子的时候,需要同时考虑“工期短”、“质量优”、“成本低”等目标。 对于多目标优化问题,往往是不能拆解成若干个单独的最优化问题来求解的;因为各个目标之间也存在着制约、矛盾的关系。 (6)博弈论(Game Theory) 往往有多方决策者参与,且信息分布是不对称的(你不知道别人在想什么),也就是说你只能拿到局部信息。 二. 最优化的基础概念 1. 凸集
根据凸集的数学定义,其实质含义为—— 如果一个空间集合为凸集,那么这个集合中的任意两点的连线,也应该在这个空间集合的内部。 凸集举例: X = {x| ||x||2≤5,且x∈R2},表示二维平面上一个以原点为圆心,半径为5的圆面。 非凸集举例: Y = {y| 2≤||y||2≤6,y∈R2},表示二维平面上一个以原点为圆心,内径和外径分别为2和6的圆环。 其中,||·||2该符号表示向量的2范数。 2. 超平面超平面是满足下面约束条件的一个点集 X = { x ∣ c T ⋅ x = z } X = \{x|c^T·x = z\} X={x∣cT⋅x=z} 其中c和z均为向量,且c≠0,z是一个常向量。 二维超平面举例: x∈R2,点集满足[1,1]·[x1,x2]T = 2,该集合对应的超平面就是二维空间中的一条直线x1+x2 = 2。 三维超平面举例: x∈R3,点集满足[1,2,3]·[x1,x2,x3]T = 2,该集合对应的超平面就是三维空间中的一个平面x1+2x2+3x3 = 2。 如果定义出了一个超平面,那么超平面就会将其所在空间划分成两个部分,其中一部分是{x|cT·x ≤z};另外一部分就是{x|cT·x >z}。 3. 凸集某一边界点的支撑超平面给定一个凸集X,且取该集合中的一个边界点w,若称一个超平面cTx = z是该边界点w的支撑超平面,则需要满足: cTw = z(该超平面是经过该边界点的)cTx≥z(或者是cTx≤z) 对于所有的x∈Z(该凸集内的所有点都分布在该支撑超平面的同一侧)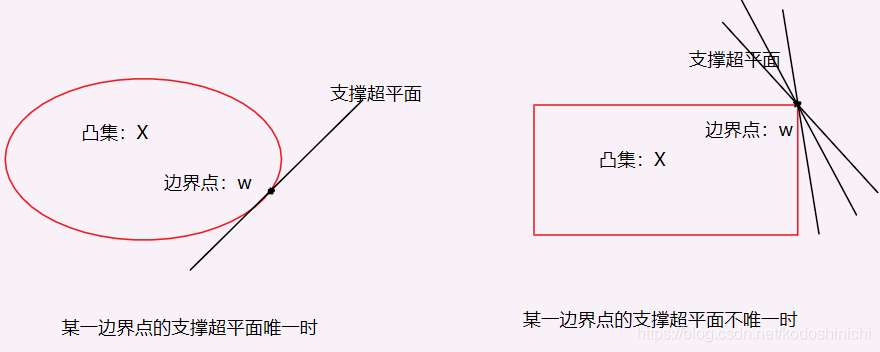 4. 凸函数(与凹函数)
4. 凸函数(与凹函数)
“定义在凸集上,且任意两个自变量的线性组合的函数值不大于该两个自变量函数值的线性组合”,这样的函数就称为凸函数。 (1)定义 【微积分中的知识回顾】 为了后续的理解与计算,现将“微分”、“方向导数”的概念进行回顾。
在定义凸函数的时候我们并不限制函数f(x)一定是可导的,但是这里我们只对于可导的函数进行性质讨论。 (1)定理一 如果f(x)是定义在凸集X上的一个可微函数,则f(x)是凸函数的充要条件是 f(x2)-f(x1)≥▽f(x1)T·(x2-x1) (2)定理二 如果f(x)是定义在凸的开集X上的一个二阶可微的函数,则f(x)是凸函数的充要条件为 f(x)对应的Hessian矩阵H(x),对于任意一个x都是半正定的。 【背景知识补充】 开集:对于集合中的任意一点,都能找到该点的一个邻域,且该邻域一定在集合内部。 可以近似地认为所谓开集就是“没有边界的集合”,e.g. {x|满足||x||2<5}就是开集,如果“ |
【本文地址】
今日新闻 |
推荐新闻 |


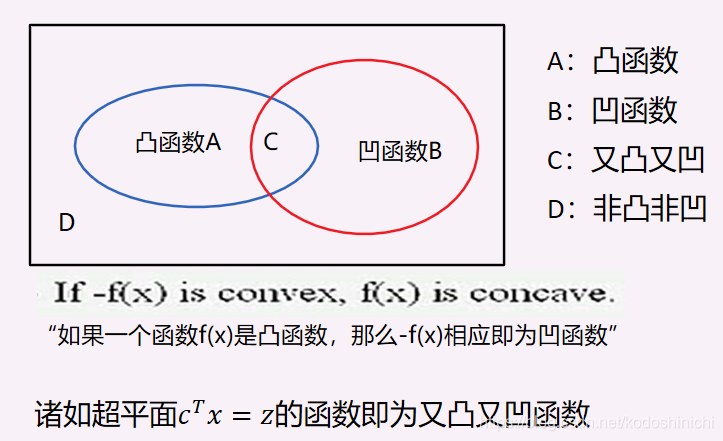
 (2)凸/凹/非凸非凹/又凸又凹函数
(2)凸/凹/非凸非凹/又凸又凹函数