哈密顿算子与梯度、散度、旋度 |
您所在的位置:网站首页 › 公式中的倒v是什么意思 › 哈密顿算子与梯度、散度、旋度 |
哈密顿算子与梯度、散度、旋度
|
哈密顿算子 点乘 叉乘
1、定义与性质
哈密顿算子:(数学符号: ∇ \nabla ∇(又称nabla,奈布拉算子)),读来作Hamilton。 向量微分算子: ∇ = ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ + ∂ ∂ z k ⃗ \nabla=\frac{\partial }{\partial x}\vec{i}+\frac{\partial}{\partial y} \vec{j}+\frac{\partial }{\partial z}\vec{k} ∇=∂x∂i +∂y∂j +∂z∂k 性质: 矢量性微分算子只对算子 ∇ \nabla ∇右边的量发生微分作用麦克斯韦方程的微分形式: ∂ D x ∂ x + ∂ D y ∂ y + ∂ D z ∂ z = ρ \frac{\partial D_{x}}{\partial x}+\frac{\partial D_{y}}{\partial y}+\frac{\partial D_{z}}{\partial z}=\rho ∂x∂Dx+∂y∂Dy+∂z∂Dz=ρ ∂ B x ∂ x + ∂ B y ∂ y + ∂ B z ∂ z = 0 \frac{\partial B_{x}}{\partial x}+\frac{\partial B_{y}}{\partial y}+\frac{\partial B_{z}}{\partial z}=0 ∂x∂Bx+∂y∂By+∂z∂Bz=0 ∂ H z ∂ y − ∂ H y ∂ z = δ x + ∂ D x ∂ t \frac{\partial H_{z}}{\partial y} -\frac{\partial H_y}{\partial z} = \delta_{x}+\frac{\partial D_{x}}{\partial t} ∂y∂Hz−∂z∂Hy=δx+∂t∂Dx ∂ H x ∂ z − ∂ H z ∂ x = δ y + ∂ D y ∂ t \frac{\partial H_{x}}{\partial z}-\frac{\partial H_{z}}{\partial x}=\delta_{y}+\frac{\partial D_{y}}{\partial t} ∂z∂Hx−∂x∂Hz=δy+∂t∂Dy ∂ H y ∂ x − ∂ H x ∂ y = δ z + ∂ D z ∂ t \frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}=\delta_{z}+\frac{\partial D_{z}}{\partial t} ∂x∂Hy−∂y∂Hx=δz+∂t∂Dz ∂ E z ∂ y − ∂ E y ∂ z = − ∂ B x ∂ t \frac{\partial E_{z}}{\partial y}-\frac{\partial E_{y}}{\partial z}=-\frac{\partial B_{x}}{\partial t} ∂y∂Ez−∂z∂Ey=−∂t∂Bx ∂ E x ∂ z − ∂ E z ∂ x = − ∂ B y ∂ t \frac{\partial E_{x}}{\partial z}-\frac{\partial E_{z}}{\partial x}=-\frac{\partial B_{y}}{\partial t} ∂z∂Ex−∂x∂Ez=−∂t∂By ∂ E y ∂ x − ∂ E x ∂ y = − ∂ B z ∂ t \frac{\partial E_{y}}{\partial x}-\frac{\partial E_{x}}{\partial y}=-\frac{\partial B_{z}}{\partial t} ∂x∂Ey−∂y∂Ex=−∂t∂Bz 引进哈密顿算子,上式简化为: { ∇ ⋅ D ⃗ = ρ ∇ ⋅ B ⃗ = 0 ∇ × H ⃗ = δ ⃗ + ∂ D ⃗ ∂ t ∇ × E ⃗ = − ∂ B ⃗ ∂ t \begin{cases} \nabla \cdot \vec{D}=\rho \\ \nabla \cdot \vec{B}=0 \\ \nabla \times \vec{H}=\vec{\delta}+\frac{\partial \vec{D}}{\partial t} \\ \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t} \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧∇⋅D =ρ∇⋅B =0∇×H =δ +∂t∂D ∇×E =−∂t∂B 2、标量场的梯度笛卡尔坐标系下的梯度: ∇ P = ∂ P ∂ x i ⃗ + ∂ P ∂ y j ⃗ + ∂ P ∂ z k ⃗ = g r a d P \nabla{P}=\frac{\partial P}{\partial x} \vec{i}+\frac{\partial P}{\partial y} \vec{j}+\frac{\partial P}{\partial z} \vec{k}=gradP ∇P=∂x∂Pi +∂y∂Pj +∂z∂Pk =gradP (结果为矢量) 3、矢量场的散度∇ ∙ V ⃗ = ∂ V x ∂ x + ∂ V y ∂ y + ∂ V z ∂ z = d i v V ⃗ \nabla \bullet \vec{V}=\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{y}}{\partial y}+\frac{\partial V_{z}}{\partial z}=div \vec{V} ∇∙V =∂x∂Vx+∂y∂Vy+∂z∂Vz=divV (结果为标量) 4、矢量场的旋度笛卡尔坐标系下旋度定义: ∇ × V ⃗ = ∣ i ⃗ j ⃗ k ⃗ ∂ ∂ x ∂ ∂ y ∂ ∂ z V x V y V z ∣ = ( ∂ V z ∂ y − ∂ V y ∂ z ) i ⃗ + ( ∂ V x ∂ z − ∂ V z ∂ x ) j ⃗ + ( ∂ V y ∂ x − ∂ V x ∂ y ) k ⃗ = r o t V ⃗ \nabla \times \vec{V}=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ V_{x} & V_{y} & V_{z} \end{array}\right| = \left(\frac{\partial V_z}{\partial y} -\frac{\partial V_{y}}{\partial z}\right) \vec{i}+\left(\frac{\partial V_{x}}{\partial z}-\frac{\partial V_{z}}{\partial x}\right) \vec{j}+\left(\frac{\partial V_{y}}{\partial x}-\frac{\partial V_{x}}{\partial y}\right) \vec{k} = rot \vec{V} ∇×V =∣∣∣∣∣∣i ∂x∂Vxj ∂y∂Vyk ∂z∂Vz∣∣∣∣∣∣=(∂y∂Vz−∂z∂Vy)i +(∂z∂Vx−∂x∂Vz)j +(∂x∂Vy−∂y∂Vx)k =rotV (结果为矢量) 5、哈密顿算子重要运算性质∇ ⋅ ( A ⃗ × B ⃗ ) = B ⃗ ⋅ ∇ × A ⃗ − A ⃗ ⋅ ∇ × B ⃗ \nabla \cdot(\vec{A} \times \vec{B})=\vec{B} \cdot \nabla \times \vec{A}-\vec{A} \cdot \nabla \times \vec{B} ∇⋅(A ×B )=B ⋅∇×A −A ⋅∇×B 证明 6、向量内积与外积的性质与几何意义向量内积的性质: a^2 ≥ 0;当a^2 = 0时,必有a = 0. (正定性)a·b = b·a. (对称性)(λa + μb)·c = λa·c + μb·c,对任意实数λ, μ成立. (线性)cos∠(a,b) =a·b/(|a||b|).|a·b| ≤ |a||b|,等号只在a与b共线时成立.内积(点乘)的几何意义包括: 表征或计算两个向量之间的夹角b向量在a向量方向上的投影向量外积的性质 a × b = -b × a. (反称性)(λa + μb) × c = λ(a ×c) + μ(b ×c). (线性)向量外积的几何意义 在三维几何中,向量a和向量b的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于a和b向量构成的平面。 在3D图像学中,外积的概念非常有用,可以通过两个向量的外积,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。如下图所示: 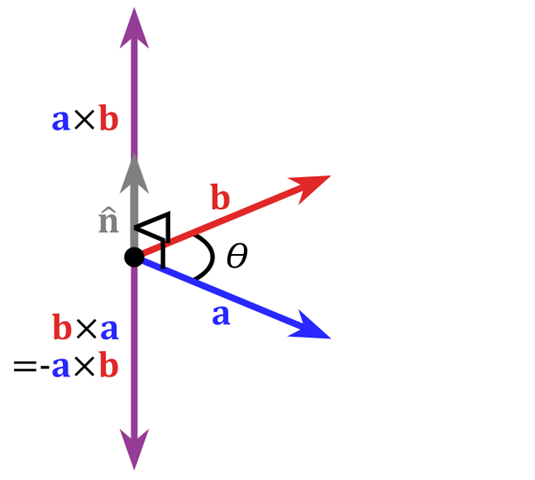 在二维空间中,外积还有另外一个几何意义就是:|a×b|在数值上等于由向量a和向量b构成的平行四边形的面积。
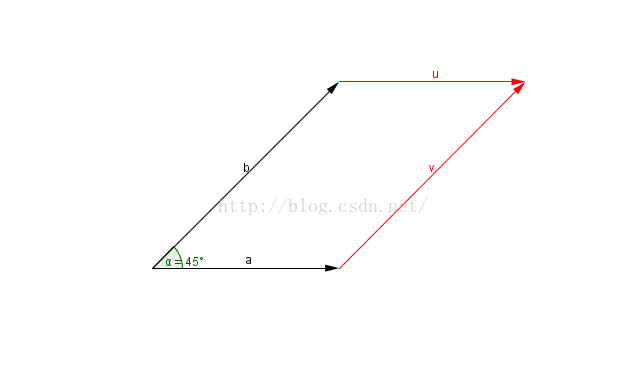
在二维空间中,外积还有另外一个几何意义就是:|a×b|在数值上等于由向量a和向量b构成的平行四边形的面积。
 7、矢量分析中常用恒等式
7、矢量分析中常用恒等式
参考 |
【本文地址】
