终于有机会可以把傅里叶分析推导一遍了。其实我对傅里叶变换一直停留在认识层面，今天就要好好梳理一下，为什么这么多人要用它来处理信号，它到底有什么魔力。

好，那我们就从傅里叶级数开始吧。

傅里叶级数公式： x ( t ) = ∑ k = − ∞ + ∞ a k e j k w 0 t              （ 1 ） x(t) = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}{e^{jk{w_0}t}}} \;\;\;\;\;\; （1） x(t)=k=−∞∑+∞​ak​ejkw0​t（1） 为什么上述公式需要用 e j k w 0 t {e^{jk{w_0}t}} ejkw0​t而不用其他呢？ e j k w 0 t = cos ⁡ ( k w 0 t ) + j sin ⁡ ( k w 0 t ) {e^{jk{w_0}t}}={\cos (k{w_0}t) + j\sin (k{w_0}t)} ejkw0​t=cos(kw0​t)+jsin(kw0​t) 是由不同频率的正弦函数构成的。在自然界中，正弦是最普遍的现象，且易于表达和计算，所以首选是正弦函数。**傅里叶分析的基本思想是想将所有任意复杂的函数，都通用的表示为一组谐波相关的复指数。**对 e j k w 0 t {e^{jk{w_0}t}} ejkw0​t在一个周期内进行积分，可以得到 ∫ T 0 e j k w 0 t d t = ∫ T 0 ( cos ⁡ ( k w 0 t ) + j sin ⁡ ( k w 0 t ) ) d t = { T 0            k = 0 0                k ≠ 0 \int_{{T_0}} {{e^{jk{w_0}t}}dt = \int_{{T_0}} {(\cos (k{w_0}t) + j\sin (k{w_0}t)} )dt = \left\{ \begin{array}{l} {T_0}\;\;\;\;\;k = 0\\ 0\;\;\;\;\;\;\;k \ne 0 \end{array} \right.} ∫T0​​ejkw0​tdt=∫T0​​(cos(kw0​t)+jsin(kw0​t))dt={T0​k=00k​=0​ 积分结果非常的简单。 所以，在傅里叶级数中，只需要求出系数 a k a_k ak​就可以了。 对于周期函数， ∫ T 0 x ( t ) e − j n w 0 t d t = ∫ T 0 e − j n w 0 t ∑ k = − ∞ + ∞ a k e j k w 0 t d t                                                        = ∑ k = − ∞ + ∞ a k ∫ T 0 e j ( k − n ) w 0 t d t                                                           = { a k T 0            k = n 0                k ≠ n \begin{array}{l} \int_{{T_0}} {x(t){e^{ - jn{w_0}t}}dt} = \int_{{T_0}} {{e^{ - jn{w_0}t}}\sum\limits_{k = - \infty }^{ + \infty } {{a_k}{e^{jk{w_0}t}}} } dt \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}\int_{{T_0}} {{e^{j(k - n){w_0}t}}} dt} \; \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \left\{ \begin{array}{l} {a_k}{T_0}\;\;\;\;\;k = n\\ 0\;\;\;\;\;\;\;k \ne n \end{array} \right. \end{array} ∫T0​​x(t)e−jnw0​tdt=∫T0​​e−jnw0​tk=−∞∑+∞​ak​ejkw0​tdt=k=−∞∑+∞​ak​∫T0​​ej(k−n)w0​tdt={ak​T0​k=n0k​=n​​ 即 ⇒ a n = 1 T 0 ∫ T 0 x ( t ) e − j n w 0 t d t \Rightarrow {a_n} = \frac{1}{{{T_0}}}\int_{{T_0}} {x(t){e^{ - jn{w_0}t}}dt} ⇒an​=T0​1​∫T0​​x(t)e−jnw0​tdt

由于计算机无法处理无限长的函数，所以要进行截断。 现要处理非周期函数，利用上面周期函数得到的结论进行进一步的推导。

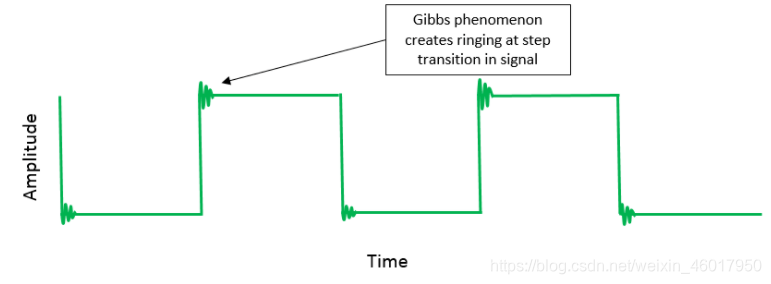
定义部分时间函数： x N ( t ) = ∑ k = − N N a k e j k w 0 t {x_N}(t) = \sum\limits_{k = - N}^N {{a_k}{e^{jk{w_0}t}}} xN​(t)=k=−N∑N​ak​ejkw0​t。 当 N → ∞ N \to \infty N→∞时， x N ( t ) {x_N}(t) xN​(t)是否和 x ( t ) x(t) x(t)一致。这里引出狄利赫里条件，即 ①在一个周期内，间断点数目有限，且为第一类间断点； ②在一个周期内，极大值极小值数目有限； ③在一个周期内，信号能量有限。 所以说，信号在每个连续点上都可以和 x ( t ) x(t) x(t)一致。在不连续点处，会有误差，这是吉布斯效应，如下图所示。

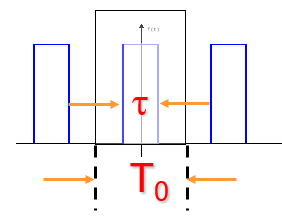以 T 0 T_0 T0​为周期，将它复制成周期信号 x ~ ( t ) \tilde x(t) x~(t)， x ~ ( t ) = x ( t ) , ∣ t ∣ < T 0 2 \tilde{x}(t)=x(t),|t|{a_k}{e^{jk{w_0}t}}}\;\;\;\;\;\;\;\;\;（2） {{T_0}}}\int_{ - {T_0}/2}^{{T_0}/2} {\tilde x(t){e^{ - jk{w_0}t}}dt} {{T_0}}}\int_{ - \infty }^\infty {x(t){e^{ - jk{w_0}t}}dt} {a_k}{e^{jk{w_0}t}}} \\\;\;\;\;\;\;\;\;{\rm{ = }}\sum\limits_{k = - \infty }^{ + \infty } {\frac{1}{{{T_0}}}X(k{w_0}){e^{jk{w_0}t}}} \\\;\;\;\;\;\;\;\; = \sum\limits_{k = - \infty }^{ + \infty }\frac{{w_0}}{{2\pi }} {X(k{w_0}){e^{jk{w_0}t}}} \end{array} {2\pi }}\int_{ - \infty }^{ + \infty } {X(w){e^{jwt}}dw} {{T_0}}}\int_{{T_0}} {x(t){e^{ - jk{w_0}t}}dt} {a_k}{e^{jk{w_0}t}}} {2\pi }}\int_{ - \infty }^{ + \infty } {X(w){e^{jwt}}dw}