超平面,半空间,多面体,单纯形定义与解析 |
您所在的位置:网站首页 › 什么叫做解析法的定义 › 超平面,半空间,多面体,单纯形定义与解析 |
超平面,半空间,多面体,单纯形定义与解析
|
深入理解仿射集,凸集,锥等定义及相关证明,这里列出一些常用的凸集,和一些球,空间,多面体,单纯形之类的正式定义,并讨论他们和凸集的关系。 R n 空 间 与 子 空 间 \color{red}\mathbf{R^n空间与子空间} Rn空间与子空间 他既是凸集,也是仿射集,也是凸锥。那么如果我们任意的选择一个子空间,他是否还满足上述性质? 定义: R n R^n Rn空间的子空间:子空间一定具有原点,子空间中的任意加减和标量乘法操作都落在子空间内部。x,y轴即是二维空间的一维子空间。因此任意的子空间仍然既是凸集,也是仿射集,也是凸锥。 任意直线 \color{red}\textbf{任意直线} 任意直线 过原点的直线是二维空间的一维子空间,因此其一定满足既是凸集,也是仿射集,也是凸锥。但是如果他不过原点,那他不是凸锥,但是是凸集和仿射集。 任意线段 \color{red}\textbf{任意线段} 任意线段 任意线段都是凸集,线段往往不是仿射集,也不是凸锥,当线段缩减为一个点的时候,他是一个仿射集,当线段缩减为一个点而且是原点的时候,他是一个凸锥。 { x 0 + θ V ∣ θ ≥ 0 } x 0 ∈ R n ; θ ∈ R ; V ∈ R n \color{red}\mathbf{\{x_0+\theta V|\theta\geq 0\}x_0\in R^n\;;\theta\in R\;;V\in R^n} {x0+θV∣θ≥0}x0∈Rn;θ∈R;V∈Rn 这是个什么东西呢?这是一个射线,从 x 0 x_0 x0开始沿着 V V V的方向的射线。一般情况他不是仿射集,当他缩减为一个点的时候,它会成为一个仿射集。任意情况下她都是一个凸集。
超平面与半空间
\color{red}\textbf{超平面与半空间}
超平面与半空间
H
y
p
e
r
p
l
a
n
e
:
{
x
∣
a
T
x
=
b
}
x
,
a
∈
R
n
;
b
∈
R
;
a
!
=
0
Hyperplane:\{x|a^Tx=b\}x,a\in R^n;b\in R;a!=0
Hyperplane:{x∣aTx=b}x,a∈Rn;b∈R;a!=0 所谓的超平面是一个集合,超平面不局限于二维的平面,下面的直线就是二维空间的超平面,三维空间的超平面是一个平面,思维空间的超平面则是立体的空间。 球 \color{red}\textbf{球} 球 B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 ≤ r } = { x ∣ ( x − x c ) T ( x − x c ) } ; x c ∈ R n , r ∈ R B(x_c,r)=\{x|||x-x_c||_2\leq r\}=\{x|\sqrt{(x-x_c)^T(x-x_c)}\};x_c\in R^n,r\in R B(xc,r)={x∣∣∣x−xc∣∣2≤r}={x∣(x−xc)T(x−xc) };xc∈Rn,r∈R 球的定义是显而易见的。球一定是一个凸集,一般不是仿射集(除非半径为0),一般不是凸锥(除非半径为0且落在原点上。) 凸集证明 \color{red}\textbf{凸集证明} 凸集证明 为了证明球是一个凸集,我们需要验证以下不等式是成立的 ∣ ∣ θ x 1 + ( 1 − θ ) x 2 − x c ∣ ∣ 2 ≤ r ||\theta x_1+(1-\theta )x_2-x_c||_2\leq r ∣∣θx1+(1−θ)x2−xc∣∣2≤r 也就是任意选择两个点的线性组合的减去圆心的二模依旧是在圆内部的,这里我们需要用到三角不等式 ∣ ∣ a + b ∣ ∣ ≤ ∣ ∣ a ∣ ∣ + ∣ ∣ b ∣ ∣ ||a+b||\leq ||a||+||b|| ∣∣a+b∣∣≤∣∣a∣∣+∣∣b∣∣,于是我们得到 ∣ ∣ θ x 1 + ( 1 − θ ) x 2 − x c ∣ ∣ 2 ≤ ∣ ∣ θ ( x 1 − x c ) ∣ ∣ + ∣ ∣ ( 1 − θ ) ( x 2 − x c ) ∣ ∣ ≤ r ||\theta x_1+(1-\theta )x_2-x_c||_2\leq ||\theta(x_1-x_c)||+||(1-\theta)(x_2-x_c)||\leq r ∣∣θx1+(1−θ)x2−xc∣∣2≤∣∣θ(x1−xc)∣∣+∣∣(1−θ)(x2−xc)∣∣≤r。 椭球 \color{red}\textbf{椭球} 椭球 E ( x c , P ) = { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } ; x c ∈ R n , P ∈ S + + n E(x_c,P)=\{x|(x-x_c)^TP^{-1}(x-x_c)\leq 1\};x_c\in R^n,P\in S^n_{++} E(xc,P)={x∣(x−xc)TP−1(x−xc)≤1};xc∈Rn,P∈S++n S + + n S^n_{++} S++n,表示对称的正定矩阵(正定矩阵即特征值全部大于0)。上面的椭球其实也是一个二范数,只不过它通过 P P P矩阵进行了加权。这个P矩阵描述的是椭球的半轴长,如果P是二维的,那么他有两个奇异值,这两个奇异值分别对应椭球的一个半轴长。
多面体polyhedron \color{red}\textbf{多面体polyhedron} 多面体polyhedron P = { x ∣ a j T x ≤ b j , j = 1... m ; c j T x = d j , j = 1... n } P=\{x|a_j^Tx\leq b_j,j=1...m;c_j^Tx=d_j,j=1...n\} P={x∣ajTx≤bj,j=1...m;cjTx=dj,j=1...n} 注意他的限制条件, a j T x ≤ b j a_j^Tx\leq b_j ajTx≤bj是半空间的约束条件, c j T x = d j , c_j^Tx=d_j, cjTx=dj,是超平面的约束条件,因此多面体实际上是一系列的半空间和超平面的交集。 需要注意的是,多面体不一定是有界的,考虑只有半空间的限制条件 a j T x ≤ b j a_j^Tx\leq b_j ajTx≤bj那么这个多面体其实就是一个半空间。那么对于我们常见的多面体(在固定范围内的面积有限的多面体我们称之为有限多面体),多面体是凸集。
单纯形simplex
\color{red}\textbf{单纯形simplex}
单纯形simplex
R
n
R^n
Rn空间中选择
v
0
,
.
.
.
,
v
k
v_0,...,v_k
v0,...,vk共
k
+
1
k+1
k+1个点,如果满足限制条件
v
1
−
v
0
,
.
.
.
,
v
k
−
v
0
\color{blue}v_1-v_0,...,v_k-v_0
v1−v0,...,vk−v0线性无关,则与上述点相关的单纯形为
C
=
C
o
n
V
{
v
0
,
.
.
.
,
v
k
}
=
{
θ
0
v
0
+
.
.
.
+
θ
k
v
k
}
;
∀
θ
i
>
0
,
∑
i
=
1
n
θ
i
=
1
C= ConV\{v_0,...,v_k\}=\{\theta_0v_0+...+\theta_kv_k\};\forall \theta_i>0,\sum_{i=1}^n\theta_i=1
C=ConV{v0,...,vk}={θ0v0+...+θkvk};∀θi>0,i=1∑nθi=1
C
o
n
V
ConV
ConV是凸包的定义,从这些点构造出来的凸包,对二维空间而言,两个点的单纯性就是他们之间的线段,三个点的单纯形(三点不共线)他们的单纯形就是一个三角形,二维空间中任意两个向量可以表示另一个向量,所以不存在四个点以上可以构造出单纯形。 证 明 : 单 纯 形 是 多 面 体 的 一 种 证明:单纯形是多面体的一种 证明:单纯形是多面体的一种 对于一个单纯形,我们有 C = C o n V { v 0 , . . . , v k } = { θ 0 v 0 + . . . + θ k v k } ; ∀ θ i > 0 , ∑ i = 1 n θ i = 1 C= ConV\{v_0,...,v_k\}=\{\theta_0v_0+...+\theta_kv_k\};\forall \theta_i>0,\sum_{i=1}^n\theta_i=1 C=ConV{v0,...,vk}={θ0v0+...+θkvk};∀θi>0,∑i=1nθi=1, v 1 − v 0 , . . . , v k − v 0 v_1-v_0,...,v_k-v_0 v1−v0,...,vk−v0线性无关。我们定义 [ θ 1 , θ 2 , . . . , θ k ] T = y , y ≥ 0 , 1 T y ≤ 1 [\theta_1,\theta_2,...,\theta_k]^T=y,y\geq 0,1^Ty\leq 1 [θ1,θ2,...,θk]T=y,y≥0,1Ty≤1 注意上面我们把 θ 0 \theta_0 θ0去掉了,因此结果小于1而不是等于1. 定义: [ v 1 − v 0 , . . . , v k − v 0 ] = B ∈ R n ∗ k [v_1-v_0,...,v_k-v_0]=B\in R^{n*k} [v1−v0,...,vk−v0]=B∈Rn∗k 此时,对于任意的 x ∈ C x\in C x∈C,我们可以写为 x = θ 0 v 0 + . . . + θ k v k x=\theta_0 v_0+...+\theta_k v_k x=θ0v0+...+θkvk这样一个凸组合。他就等价于 v 0 + θ 1 ( v 1 − v 0 ) + . . . + θ k ( v k − v 0 ) = v 0 + B y \color{red}v_0+\theta_1(v_1-v_0)+...+\theta_k(v_k-v_0)=v_0+By v0+θ1(v1−v0)+...+θk(vk−v0)=v0+By。 因为
B
B
B的每个向量都是线性无关的,那么
B
B
B的秩一定等于
k
,
k
≤
n
k,k\leq n
k,k≤n,也就是一个列满秩的矩阵。那么我们可以通过线性变化将他转化为这样形式的矩阵: 那么我们将上述等式变化为
A
x
=
A
v
0
+
A
B
y
Ax=Av_0+ABy
Ax=Av0+ABy,只要这里的矩阵A是非奇异的,我们可以进行逆运算在等式两侧互相转换。精华部分来了! 对称矩阵集合 S n = { x ∈ R n ∗ n ∣ x = x T } \color{red}\textbf{对称矩阵集合 } S^n=\{x\in R^{n*n}|x=x^T\} 对称矩阵集合 Sn={x∈Rn∗n∣x=xT} 对称半正定矩阵集合 S + n = { x ∈ R n ∗ n ∣ x = x T ; x ⪰ 0 } \color{red}\textbf{对称半正定矩阵集合 } S_+^n=\{x\in R^{n*n}|x=x^T;x\succeq0\} 对称半正定矩阵集合 S+n={x∈Rn∗n∣x=xT;x⪰0} 对称正定矩阵集合 S + + n = { x ∈ R n ∗ n ∣ x = x T ; x ≻ 0 } \color{red}\textbf{对称正定矩阵集合 } S_{++}^n=\{x\in R^{n*n}|x=x^T;x\succ0\} 对称正定矩阵集合 S++n={x∈Rn∗n∣x=xT;x≻0} 注意上面不是大于号,一般用大于号表示矩阵内部元素全部大于某个值,而上面的符号表示所有特征值大于某个值,(也就是到底是非负矩阵还是半正定矩阵) 对称半正定矩阵是一个凸锥,而正定矩阵特征值不能等于零,在矩阵空间中不过原点,那么不是凸锥,但是凸集。 |
【本文地址】
今日新闻 |
推荐新闻 |
 H
a
l
f
s
p
a
c
e
Half space
Halfspace 上图中的直线分隔开来的两个部分称之为半空间,两个空间一样大(无穷级数的概念)。
H
a
l
f
s
p
a
c
e
Half space
Halfspace 上图中的直线分隔开来的两个部分称之为半空间,两个空间一样大(无穷级数的概念)。
 类似的在三维空间中最多选择四个点满足线性无关的条件,他们会构成一个四面体,在三维空间中我们不可能找到一个五面体六面体。
类似的在三维空间中最多选择四个点满足线性无关的条件,他们会构成一个四面体,在三维空间中我们不可能找到一个五面体六面体。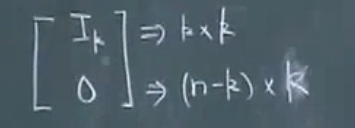
 首先我们使用A矩阵,将B拆分成上述形式(上面n*n单位阵,下面全零),此时我们可以吧该式分成两部分(也就到了式3,注意因为
A
1
B
A_1B
A1B是单位阵所以第一个等式留下了
y
y
y,而第二个等式没有
y
y
y)。此时需要注意的是,
y
y
y是可以变化的,而在单纯形的定义中,我们知道
y
≥
0
,
1
T
y
≤
1
y\geq 0,1^Ty\leq 1
y≥0,1Ty≤1,于是我们带入现在的方程,就得到了两个不等式约束,和一个等式条件,也就是说在这个单纯形内部,给定任意一个
x
x
x,我们都可以用这个式子描述,而且这个式子可以描述单纯形中任意一个
x
x
x,又因为这些约束条件都是线性约束,所以任意的一个单纯形,都是一个多面体
首先我们使用A矩阵,将B拆分成上述形式(上面n*n单位阵,下面全零),此时我们可以吧该式分成两部分(也就到了式3,注意因为
A
1
B
A_1B
A1B是单位阵所以第一个等式留下了
y
y
y,而第二个等式没有
y
y
y)。此时需要注意的是,
y
y
y是可以变化的,而在单纯形的定义中,我们知道
y
≥
0
,
1
T
y
≤
1
y\geq 0,1^Ty\leq 1
y≥0,1Ty≤1,于是我们带入现在的方程,就得到了两个不等式约束,和一个等式条件,也就是说在这个单纯形内部,给定任意一个
x
x
x,我们都可以用这个式子描述,而且这个式子可以描述单纯形中任意一个
x
x
x,又因为这些约束条件都是线性约束,所以任意的一个单纯形,都是一个多面体