拉格朗日乘子、拉格朗日对偶问题 (举例说明，通俗易懂)

您所在的位置：网站首页 › 举例说明max函数的应用 › 拉格朗日乘子、拉格朗日对偶问题 (举例说明，通俗易懂)

拉格朗日乘子、拉格朗日对偶问题 (举例说明，通俗易懂)

2024-07-09 16:02| 来源: 网络整理| 查看: 265

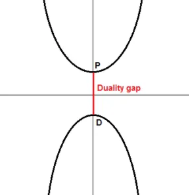
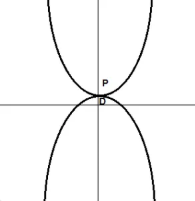
本文通过一系列的例子来说明拉格朗日乘子的运算以及原理，通俗易懂。

1、拉格朗日乘数(乘子)原理

定义：

In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints. (Wikipedia)

实际上，拉格朗日乘数法(Lagrange Multipliers)是一种求函数极值的方法。

例1：求函数 $f(x,y)=8x^2-2y$ 的极值（极大值和极小值），同时满足约束 $g(x,y)=x^2+y^2=1$ 。

解法一：直接将 $x^2=1-y^2$ 带入函数求得 y 和 x。

解法二：观察两者的图形：

左图（最大值）右图（最小值）

从上图（左）可以看出，当函数 $f(x,y)$ (红色) 与约束 $g(x,y)$ （蓝色）相切时，函数 $f(x,y)$ 取得最小值-2，此时 $(x,y)=(0,1)$ ；

从右图可以看出，也是当函数约束相切时，函数取得最大值 8.125，此时 $(x,y)=(-\frac{3\sqrt{7}}{8},-\frac{1}{8}),(\frac{3\sqrt{7}}{8},-\frac{1}{8})$ 。

由约束 $g(x,y)$ 与函数 $f(x,y)$ 相切可知，两者在切点的法向量必须平行即梯度（导数）方向是相同的，但两个梯度的大小可能会有所不同，因此引入未知常数乘数(也叫乘子) λ ( ${\color{Red} \lambda\geq 0}$ ) 是必要的，因此有：

$\bigtriangledown f(x,y)=\lambda \bigtriangledown g(x,y)$

$\left \langle {f}'_x, {f}'_y\right \rangle=\lambda \left \langle {g}'_x, {g}'_y\right \rangle$

$\left \langle {f}'_x, {f}'_y\right \rangle= \left \langle \lambda{g}'_x, \lambda{g}'_y\right \rangle$

$\left \langle \frac{\partial f(x,y)}{\partial x},\frac{\partial f(x,y)}{\partial y} \right \rangle =\left \langle \frac{\partial g(x,y)}{\partial x},\frac{\partial g(x,y)}{\partial y} \right \rangle$

$\left \langle 16x,-2 \right \rangle=\left \langle \lambda2x,\lambda2y \right \rangle$

↓↓↓↓

$\left\{\begin{matrix} 16x=\lambda2x\\ -2=\lambda2y \end{matrix}\right.\Rightarrow \left\{\begin{matrix} (8-\lambda)x=0\\ y=-\frac{1}{\lambda}\end{matrix}\Rightarrow \right.\left\{\begin{matrix} \lambda=0, y=-\frac{1}{8}, x=\pm \frac{3\sqrt{7}}{8}, f(x,y)=8.125\\ x=0,y=1,f(x,y)=-2,\lambda=...\\ x=0,y=-1, f(x,y)=2,\lambda=... \end{matrix}\right.$

由上可知，拉格朗日乘子就是引入了乘子lambda( $\lambda\geq 0$ ) ,得到函数的梯度等于约束函数的梯度的一个向量的(代数)方程，并与原始约束方程一起确定解，从而求得函数的极值。

注意：约束 $g(x,y)$ 在切点的梯度必须存在且不为零向量。

除了上述中 $\left \langle {f}'_x, {f}'_y\right \rangle= \left \langle \lambda{g}'_x, \lambda{g}'_y\right \rangle$ 的形式，拉格朗日乘子还可以用另一种方式表达。

因为只要求函数与约束的梯度（导数）相同，所以有：

$\left ({f}'_x, {f}'_y \right ) - \left (\lambda{g}'_x, \lambda{g}'_y \right ) = 0$

${f}'_x - \lambda{g}'_x=0$

${f}'_y- \lambda{g}'_y=0$

将等式用另一符号表示:

$\left ({f}'_x, {f}'_y \right ) - \left (\lambda{g}'_x, \lambda{g}'_y \right ) = 0= \bigtriangledown L(x,y)$

$\Rightarrow\bigtriangledown L(x,y, \lambda)=\left ({f}'_x, {f}'_y \right ) - \left (\lambda{g}'_x, \lambda{g}'_y \right )$

$\Rightarrow L(x,y, \lambda)=f(X,y)- \lambda (g(x,y)-c)$

↓↓↓↓

${f}'_x - \lambda{g}'_x=0\Rightarrow \frac{\partial L(x,y)}{\partial x}=0$

${f}'_y- \lambda{g}'_y=0\Rightarrow \frac{\partial L(x,y)}{\partial y}=0$

$\Rightarrow \frac{\partial L(x,y)}{\partial \lambda}=0\Rightarrow g(x,y)-c=0$

上述函数L，叫做拉格朗日算符(Lagrangian)，上式中的 c 代表常数，代表约束方程等号右边的1。

2、拉格朗日乘数(乘子)的解释

例2：假设你在假设你在经营一家工厂，生产某种需要钢铁作为原材料的小部件。人力成本(human harbor)20块每小时，钢铁(steel)每吨70元。假设你的收入（Revenue,R)是满足一下方程：

$R(h,s)=200h^{2/3}s^{1/3}$ ， h表示工时，s表示钢铁吨数

如果成本预算是在20000块，则最大可能受益是多少？

根据以上条件可得到约束方程： $20h+70s=20000$ ,绘制待求函数与约束方程的图，如下图（左）所示。

通过带入朗格朗日算符得： $L(h,s,\lambda) =200h^{2/3}s^{1/3}-\lambda(20h+70s-20000)$

对各参数求导，找到L的临界点： $\bigtriangledown L(h,s,\lambda)=0$

这个方程可能有好几个解： $(h_0,s_0,\lambda_0),(h_1,s_1,\lambda_1),(h_2,s_2,\lambda_2),...$ ,对于每个解带入 $R(h,s)$ 看看哪一个符合最大值。

通常把临界点的最大值写成 $(h^*,s^*,\lambda^*)$ ，使用星号上标来表示这是一个解决方案。 $h^*,s^*$ 表示根据预算最大化收入时应该分配的劳动小时数和钢材吨数。但如何理解最大化值的拉格朗日乘子 $\lambda^*$ ？ ${\color{Red}\mathbf{ \lambda^*}}$ 表示通过改变预算可以多赚多少钱。

左中右

假设预算为变量b,则 $20h+70s=b$ ，如上图（中）所示，红色直线表示的是 $b=20000$ 时的状态。若预算 b 可在 15000-25000内取值，则对于每个b值都可以最大化 $R(h,s)$ ，所当最大值 $R(h,s)$ 变化时，b也在变化，对这种变化进行研究。

用 $M^*$ 表示最大收益，当只改变 b 时， $M^*$ 的变化如上图（右）所示，所以最大收益 $M^*$ 是关于预算 b 的函数，可以写成 $M^*(b)$ ，对 b 求导得：

$\frac{\partial M(b)}{\partial b}=\lambda^*(b)$

因此， $\lambda^*(b)$ 表示黑点 $M^*$ 相对于绿点 b 移动时的变化率（上图（右））。理解起来有点困难，对于这个例子的 $b=20000$ 时的最大收益对应的 $\lambda^*(b)=2.59$ ，表示预算每增加额外的1元，收益会增加2.59元；预算每下降1元，收益减少2.59美元。

3、拉格朗日对偶(duality)问题

对偶定义：

In mathematical optimization theory, duality means that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem (the duality principle). The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem. (Wikipedia)

对下界的理解（lower bound）：假设有一集合 $S=\left \{ 2,4,8,12 \right \}$ ，求其下界。

因为集合S的最小值为2，所有小于等于2的值均可为集合S的下界 (lower bound)，如1，-3等等。但2是集合S的最大下界，因为其比其他任何下界都要大，因此又叫最大下界(infimum or greatest lower bound)，最大下界有且仅有一个。

同样的是，延伸到S集合的最大值12，所有大于等于12的值均可为集合S的上界 (upper-bound)，其有最小上界12(supremum)。

通过对偶的定义可以知道，如果有一个最小化问题，则可以把它看做一个最大化问题。最大化问题的最大值就是最小化问题的下界，其永远小于等于最小化问题的最小值。

为什么要用对偶性(duality)?因为有时，解对偶问题( dual problem)比解原始问题(primal problem)简单。

关于下界，对于某些问题，解对偶问题的结果与解原问题的结果是一样的。

如下图（左）所示，对于原始问题，尝试去最小化方程，得到最小值P。通过对偶方程求解，得到最大值点D。从图中可以看出，点D是原始问题的下界。定义 $P-D$ 为对偶间隙(duality gap)。该例中 $P-D0$ 称为弱对偶性持有(weak duality holds)。

从下图（右）可以看出， $P-D=0$ ，没有对偶间隙，称为强对偶性持有(strong duality holds)。

带约束的最优化问题:

一个优化问题的典型写法如下：

minimize(x) $f(x)$

subject to $g_i(x)=0,i=1,...,p$

$h_j(x)\leq 0,j=1,...,m$

上式是优化问题的标准形式，还有一些其他形式。

$f$ 叫做目标函数 (objective function) 有时也叫损失函数 (cost function)。通过改变 $x$ 来找到 $f$ 的最小值对应的 $x^*$ 。

函数 $g_i$ 叫做等式约束 (equality constraints)，函数 $h_i$ 叫做不等式约束 (inequality constraints)。 $x^*$ 必须满足上述约束。

当存在多个约束时，它们都必须为真。

拉格朗日优化函数为：

$L(x,\lambda,\mu)=f(x)+\sum_{i=1}^p\lambda_ig_i(x)+\sum_{j=1}^p\mu_jh_j(x)$

如果 $h_j(x)\geq 0$ ，上式中就用减号，始终保持 $L(x,\lambda,\mu)$ 是用来求最小值，同时注意等式和不等式约束等号和不等号右边恒为常数0，若是不为0的常数，移到等号和不等号左边再构建拉格朗日函数。

假设函数 $f(x)$ 的 x 取值集合为 $\chi$ ，则在等式和不等式约束条件下函数 $f(x)$ 的可行集(feasible set)为：

$R=\left \{ x\in \chi |g(x)=0,h(x)\leq 0 \right \}$

则最优解：

$x^*=\inf\left \{ f(x)|g_i(x)=0,i=1,...,p,h_j(x)\leq 0,j=1,..,m \right \}, \inf=infimum$

基本上，它就是用数学符号表示最优值是 $f(x)$ 在所有约束条件下的最小值(infimum)。

进一步分析，因为 $g_i(x)=0,h_j(x)\leq 0,\lambda_i\geq 0,\mu_i\geq 0$ ，所以有：

$L(x,\lambda,\mu)=\inf \left \{ f(x^*)+\sum_{i=1}^p\lambda_ig_i(x^*)+\sum_{j=1}^p\mu_jh_j(x^*) \right \}$

$\leq \min f(x)+\sum_{i=1}^p\lambda_ig_i(x)+\sum_{j=1}^p\mu_jh_j(x)$

$\leq \min f(x)$

对于上式可以这么理解，需要优化的函数 $f(x)$ 在所有约束下的最小值 $\min f(x)$ 恒大于等于拉格朗日函数 $L(x,\lambda,\mu)$ ，根据上面下界的理解可知， $\min f(x)$ 是恒大于拉格朗日函数的最大值 $(\max L(x,\lambda,\mu))$ 的。

进一步推导可以得到(sup表示函数的上界即最大值）：

$\inf\left \{ f(x)|g_i(x)=0,h_j(x)\leq 0,\right \}\geq \sup \left \{ L(x,\lambda,\mu) \right \}\widehat{}$

由推论可知，原问题的最优目标值大于或等于对偶问题的最优目标值。如果不等式是严格不等式，那么它就存在对偶性缺口（上图左）。

4、应用于支持向量机

拉格朗日乘子有时被称为不确定乘数(undetermined multipliers)，是用来找出一个多变量函数在一个或多个约束条件下的固定点(stationary points)。

已知线性支持向量机的线性模型为： $y(x)=w^T\phi (x)+b=w^Tx+b$

其拉格朗日方程为(拉格朗日乘子用a表示，同上面的lambda)：

$L(w,b,a)=\frac{1}{2}||w||^2-\sum_{n=1}^Na_n \left \{ t_n(w^Tx_n+b) -1\right \},n=1,...,N$

注意 $x_1,x_2$ 都是已知的，此时函数的变量是 $w$ 。

具体推导见：https://blog.csdn.net/mengjizhiyou/article/details/103381190

Karush-Kuhn-Tucker(KKT)（5个）条件：

$\frac{\partial L}{\partial w} =w-\sum_{n=1}^Na_nt_nx_n=0$

$\frac{\partial L}{\partial b}=-\sum_{n=1}^Na_nt_n=0$

$t_ny(x_n) -1\geq 0$

$a_n\geq 0$

$a_n(t_ny(x_n) -1 )= 0$

下面通过举例说明拉格朗日乘子在SVMs中的应用。

例3：假设有两点 $x_1=(1,1),x_2=(2,2)$ ，找到一个超平面将其分成两类。

从上面支持向量机的拉格朗日函数可知:

$f(w)=\frac{1}{2}\left \| w \right \|^2$

$g(w,b)= t_n(w^Tx_n+b) -1\geq 0$

因为 $t_n\in\left \{ -1,1 \right \}$ ,所以 $g(w,b)$ 可以写成如下形式：

$g_1(w,b)=(w^Tx_1+b) -1\geq 0$

$g_2(w,b)= -(w^Tx_2+b) -1\geq 0$ $(t_1=1,t_2=-1)$

因此拉格朗日函数可以写成：

$L(w,b,a)=\frac{1}{2}||w||^2-a_1g_1(w,b)-a_2g_2(w,b)$

$=\frac{1}{2}||w||^2-a_1( (w^Tx_1+b) -1 )-a_2 (-(w^Tx_2+b)-1 )$

$=\frac{1}{2}||w||^2-a_1 ((w^Tx_1+b) -1 )+a_2 ((w^Tx_2+b) +1 )$

求解梯度方程：

$\bigtriangledown L(w,b,a)=\bigtriangledown f(x)-a_1\bigtriangledown g_1(w,b)-a_2\bigtriangledown g_2(w,b)=0$

$\frac{\partial L}{\partial w} =w-a_1x_1+a_2x_2=0$

$\frac{\partial L}{\partial b} =-a_1+a_2=0$

$\frac{\partial L}{\partial a_1} = (w^Tx_1+b) -1=0$

$\frac{\partial L}{\partial a_2} = ( w^Tx_2+b) +1=0$

解法一：解析解

根据以上方程可得：

$(w^Tx_1+b) -1= (w^Tx_2+b) +1=0$

$w^Tx_1 -1= w^Tx_2 +1$

$w^Tx_1 -w^Tx_2=2$

$w^T(x_1 -x_2)=2$

$\left \langle (w_1,w_2),[(1,1)-(2,2)] \right \rangle=2$

$\left \langle (w_1,w_2),(-1,-1) \right \rangle=2$

$-w_1-w_2=2$

$w_1=-(w_2+2)$

由 $\frac{\partial L}{\partial w} =w-a_1x_1+a_2x_2=0$ ， $\frac{\partial L}{\partial b} =-a_1+a_2=0$ 可得：

$(w_1,w_2)-a_1(1,1)+a_2(2,2)=0$

$(w_1,w_2)-a_1(1,1)+a_1(2,2)=0$

$(w_1,w_2)+a_1(1,1)=0$

↓↓↓↓

$w_1+a_1=0$

$w_2+a_1=0$

↓↓↓↓

$w_1=w_2$

结合上面 $w_1=-(w_2+2)$ ，求得： $w_1=w_2=-1$ ， $a_1=a_2=1$

根据 $\frac{\partial L}{\partial a_1} = (w^Tx_1+b) -1=0$ 得：

$b= 1-w^Tx_1=1-\left \langle (w_1,w_2),(1,1) \right \rangle=1-[(-1*1)+(-1*1)]=3$

注意，上面算得的参数结果必须符合KKT条件，将参数带入那5个式子算一下是否符合条件。

例3只有两个点，可以通过上述解析解的方式求得参数，但过于复杂。通常支持向量机优化只能在训练数据量非常小的情况下解析求解或者在线性可分离得情况下并且已知哪些点是支持向量。大多数情况下，用数值解。

解法二：拉格朗日对偶

已知：

$L(w,b,a)=\frac{1}{2}||w||^2-a_1 ((w^Tx_1+b) -1 )+a_2 ((w^Tx_2+b) +1 )$

$=\frac{1}{2}||w||^2-a_1w^Tx_1-a_1b +a_1 +a_2 w^Tx_2+a_2b+a_2$

由 $\frac{\partial L}{\partial w} =w-a_1x_1+a_2x_2=0$ ， $\frac{\partial L}{\partial b} =-a_1+a_2=0$ 可得：

$L(a)=\frac{1}{2}||w||^2-a_1w^Tx_1 +a_1 +a_2 w^Tx_2+a_2+b(a_2-a_1)$

$=\frac{1}{2}(a_1x_1-a_2x_2)^2-a_1(a_1x_1-a_2x_2)x_1+a_1 +a_2 (a_1x_1-a_2x_2)x_2+a_2$

$=\frac{1}{2}(a_1x_1-a_2x_2)^2-(a_1x_1-a_2x_2)^2+a_1+a_2$

$=-\frac{1}{2}(a_1x_1-a_2x_2)^2+a_1+a_2$

因为KKT里有关于拉格朗日乘子 a 的约束：

$\frac{\partial L}{\partial b}=-\sum_{n=1}^Na_nt_n=0$

所以需要将其考虑进拉格朗日的梯度里，像上面加入约束的方式加入 $L(a)$ 得到拉格朗日的对偶函数：

$L(a,\gamma)=-\frac{1}{2}(a_1x_1-a_2x_2)^2+a_1+a_2-\gamma\sum_{n=1}^Na_nt_n$ $(t_1=1,t_2=-1)$

$=-\frac{1}{2}(a_1x_1-a_2x_2)^2+a_1+a_2-\gamma(a_1-a_2)$

对参数求导：

$\frac{L(a,\gamma)}{a_1}=-a_1\left \langle x_1,x_1 \right \rangle+a_2\left \langle x_1,x_2 \right \rangle+1-\gamma=0$

$\frac{L(a,\gamma)}{a_2}=-a_2\left \langle x_2,x_2 \right \rangle+a_1\left \langle x_1,x_2 \right \rangle+1+\gamma=0$

$\frac{L(a,\gamma)}{\gamma}=-a_1+a_2=0$

↓↓↓↓

$-a_1\times (1\times1+1\times1)+a_2\times(1\times2+1\times2)+1-\gamma=0$

$-a_2\times (2\times2+2\times2)+a_1\times(1\times2+1\times2)+1+\gamma=0$

$-a_1+a_2=0$

↓↓↓↓

$a_1=a_2=1,\gamma=3$

不需要求出gamma的具体值，因为求w和b时用不到它，将上面 $a_1,a_2$ 的结果带入下式（KKT）求出w和b，注意 $x_1,x_2$ 都是已知的。

$\frac{\partial L}{\partial w} =w-a_1x_1+a_2x_2=0$

$a_n(t_ny(x_n) -1 )= 0$

【本文地址】

拉格朗日乘子、拉格朗日对偶问题 (举例说明，通俗易懂)

拉格朗日乘子、拉格朗日对偶问题 (举例说明，通俗易懂)

今日新闻

推荐新闻