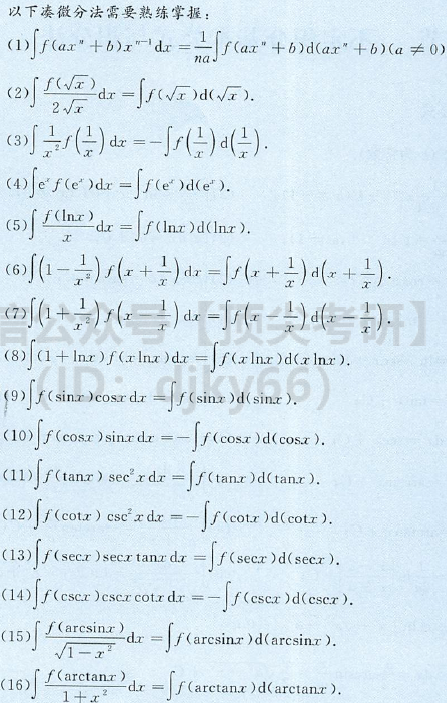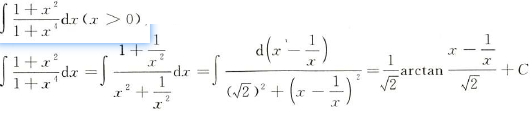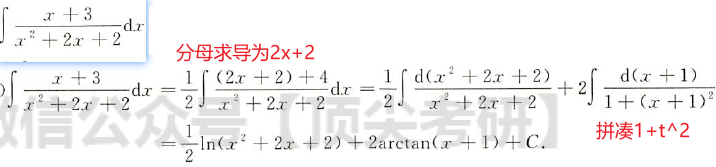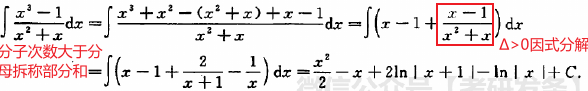不定积分及简单例题 |
您所在的位置:网站首页 › 三角函数公式及例题解析 › 不定积分及简单例题 |
不定积分及简单例题
|
文章目录
一 基本概念二 公式与积分法2.1 基本公式2.2 换元积分凑微分法换元积分法
2.3 分部积分
三 三角有理函数3.1 有理函数积分3.2 反三角求导3.3 万能公式3.4 三角函数
四 基本题型4.1 概念4.2 换元积分法4.3 分部积分4.2 有理与三角函数
五 接力题典5.1 入门5.2 基础5.3 提高
六 补充
一 基本概念
原函数 [函数] F(x)定义于I,对一切x∈I,有F’(x) = f(x)【确保可导】,则称F(x)为f(x)的原函数。 存在定理 f(x)在I区间上连续(变上限积分可导),则f(x)在I上一定存在原函数。反之不对f(x)有第一类间断点(可去、间断),则无原函数【符号函数sgn的“原函数”在x=0点不可导】;第二类间断点可能有原函数不定积分 [集合] f(x)的所有原函数F(x)+C 称为f(x)的不定积分。记为∫f(x)dx = F(x)+C。
基本性质 ∫ [ f ( x ) ± g ( x ) ] d x = ∫ f ( x ) d x ± ∫ g ( x ) d x ∫ k f ( x ) d x = k ∫ f ( x ) d x ( k ≠ 0 ) d ∫ f ( x ) d x = f ( x ) d x , ∫ d f ( x ) = f ( x ) + C \int \bigg[f(x) \pm g(x) \bigg]dx = \int f(x)dx \pm \int g(x)dx \\ \int kf(x)dx = k\int f(x)dx \quad (k\neq 0) \\ d \int f(x)dx = f(x)dx,\int df(x)=f(x)+C ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx∫kf(x)dx=k∫f(x)dx(k=0)d∫f(x)dx=f(x)dx,∫df(x)=f(x)+C 奇偶性 (以f(x)为核心,向两边推导) f’(x)f(x)F(x)偶⬅奇➡偶奇⬅偶不确定,有常数周期⬅周期不一定是周期 二 公式与积分法求完不定积分记得加一个常数C 2.1 基本公式
补充 ∫ 1 1 + cos x d x = ∫ 1 2 cos 2 ( x / 2 ) d x = ∫ sec 2 ( x / 2 ) d ( x / 2 ) = tan x 2 + c \int \frac{1}{1+\cos x}dx = \int \frac{1}{2\cos^2 (x/2)}dx = \int \sec^2 (x/2)d(x/2) = \tan \frac{x}{2}+c ∫1+cosx1dx=∫2cos2(x/2)1dx=∫sec2(x/2)d(x/2)=tan2x+c 2.2 换元积分 凑微分法φ ( x ) \varphi(x) φ(x)是可导函数, ∫ f [ φ ( x ) ] φ ′ ( x ) d x = ∫ f [ φ ( x ) ] d [ φ ( x ) ] = F [ φ ( x ) ] + C . \begin{aligned} \int f[\varphi(x)] \varphi^{\prime}(x) \mathrm{d} x =\int f[\varphi(x)] \mathrm{d}[\varphi(x)] =F[\varphi(x)]+C . \end{aligned} ∫f[φ(x)]φ′(x)dx=∫f[φ(x)]d[φ(x)]=F[φ(x)]+C. 注解:
适用于两类不同函数相乘,反对幂指 u-v‘,如反三角和ex出现时候倾向把ex放入d(ex) 推导 ( u v ) ′ = u ′ v + u v ′ u v = ∫ u ′ v d x + ∫ u v ′ d x = ∫ v d u + ∫ u d v ∫ u v ′ d x = ∫ u d v = u v − ∫ v d u \begin{aligned} &(uv)' = u'v + uv' \\ & uv = ∫ u'vdx + ∫uv'dx = ∫vdu + ∫udv\\ & ∫uv'dx = ∫udv = uv - ∫vdu \end{aligned} (uv)′=u′v+uv′uv=∫u′vdx+∫uv′dx=∫vdu+∫udv∫uv′dx=∫udv=uv−∫vdu 使用情形
注意 使用分部积分时,被积函数里ln 和 arc 只能存在一个,把另一个和其他放到后面d()里面去。 积不出 不等于 没有原函数,只是原函数不是初等函数 p(x)*三角 一般把三角放后面、p(x)反三角把p(x)放进去、ex可能要多次 【例题】2018数一
30多年只考过2、3题 有理函数概念:设R(x) = P(x)/Q(x),其中P(x),Q(x)为多项式,称R(x)为有理函数。[deg:次数] d e g P ( x ) < d e g Q ( x ) , R ( x ) 为真分式 d e g P ( x ) ≥ d e g Q ( x ) , R ( x ) 为假分式 deg P(x) < deg Q(x),R(x)为真分式 \\ deg P(x) \ge deg Q(x),R(x)为假分式 degP(x)0 因式分解 3 x − 5 ( 2 x + 1 ) ( x − 2 ) = A 2 x + 1 + B x − 2 A + 2 B = 3 , − 2 A + B = − 5 \frac{3x-5}{(2x+1)(x-2)} = \frac{A}{2x+1} + \frac{B}{x-2} \\ A+2B = 3,-2A+B = -5 \\ (2x+1)(x−2)3x−5=2x+1A+x−2BA+2B=3,−2A+B=−5 情况2 分母有平方 x 2 − 3 ( x + 1 ) 2 ( 2 x − 1 ) = A x + 1 + B ( x + 1 ) 2 + C 2 x − 1 \frac{x^2 - 3}{(x+1)^2(2x-1)} = \frac{A}{x+1} + \frac{B}{(x+1)^2} + \frac{C}{2x-1} (x+1)2(2x−1)x2−3=x+1A+(x+1)2B+2x−1C 情况3 分母中有**(ax+b)n** A 1 a x + b + A 2 ( a x + b ) 2 + . . . + A n ( a x + b ) n \frac{A_1}{ax+b}+\frac{A_2}{(ax+b)^2}+...+\frac{A_n} {(ax+b)^n} ax+bA1+(ax+b)2A2+...+(ax+b)nAn 情况4 Δ 反三角公式
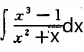
|
【本文地址】
今日新闻 |
推荐新闻 |