基于MATLAB的二维与三维插值拟合运算（附完整代码）

您所在的位置：网站首页 › 三维直线拟合 › 基于MATLAB的二维与三维插值拟合运算（附完整代码）

基于MATLAB的二维与三维插值拟合运算（附完整代码）

2024-07-11 20:22| 来源: 网络整理| 查看: 265

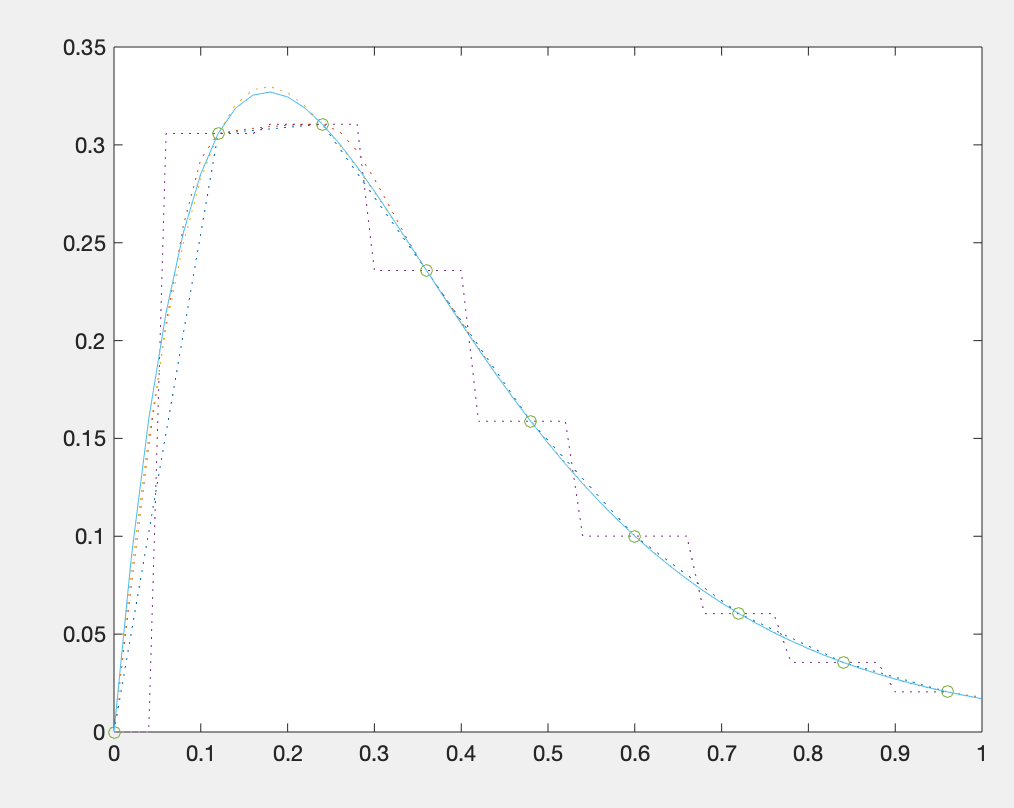
一. 一维插值

interp1函数在上个博客中（如下链接）已经更新了，此处再补充两个相关例题。

基于MATLAB的数据插值运算：Lagrange与Hermite算法（附完整代码）_唠嗑！的博客-CSDN博客

例题1

自行选择来自函数f(x)的数据点：

$f(x)=(x^2-3x+5)e^{-5x}sinx$

根据选择的数据进行插值处理，得出曲线。

解：

MATLAB代码如下：

clc;clear; x=0:0.12:1; y=(x.^2-3*x+5).*exp(-5*x).*sin(x); %调用interp1()函数 x1=0:.02:1; y0=(x1.^2-3*x1+5).*exp(-5*x1).*sin(x1); y1=interp1(x,y,x1); y2=interp1(x,y,x1,'pchip'); %分段三次Hermite插值 y3=interp1(x,y,x1,'spline'); %三次样条函数插值 y4=interp1(x,y,x1,'nearest'); %最近邻点插值 plot(x1,[y1',y2',y3',y4'],':',x,y,'o',x1,y0) %五条曲线，一个描点 %误差分析 [max(abs(y0(1:49)-y2(1:49))),max(abs(y0-y3)),max(abs(y0-y4))]

运行结果：

ans =

0.017651383860966 0.008613955066235 0.159826013541615

例题2

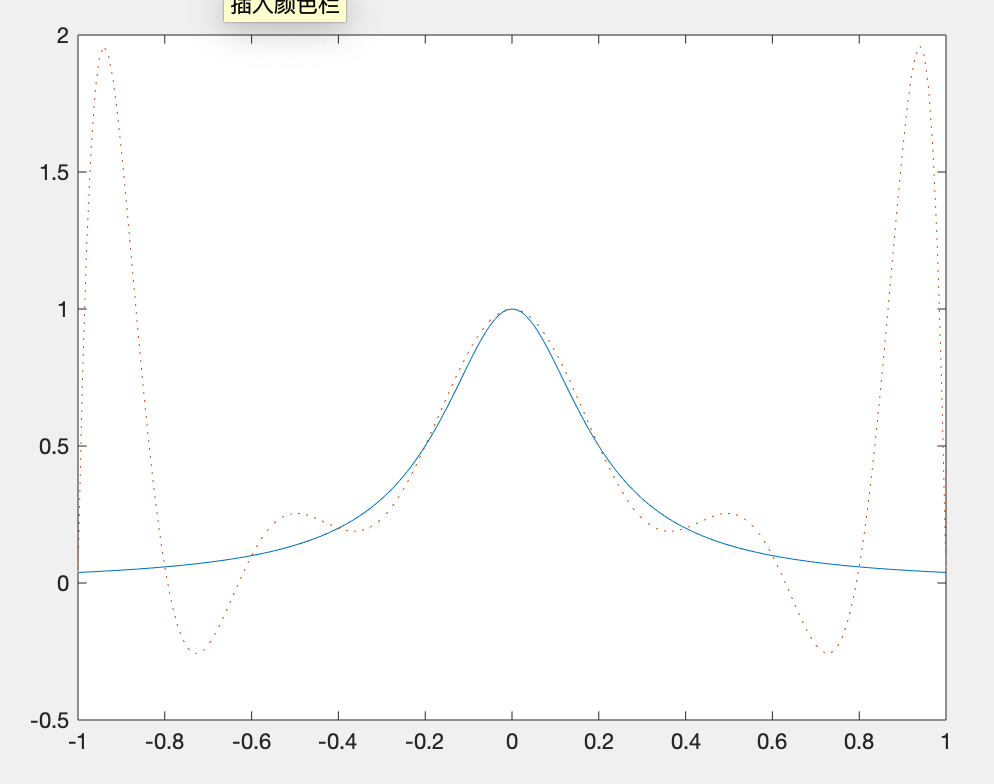
对f(x)进行Lagrange插值，并画图与标准图像对比。

$f(x)=\frac{1}{1+25x^2},\quad -1\leq x\leq 1$

解：

MATLAB代码如下：

clc;clear; x0=-1+2*[0:10]/10; y0=1./(1+25*x0.^2); %x0与y0生成数据点 x=-1:.01:1; y=lagrange(x0,y0,x); %Lagrange插值 ya=1./(1+25*x.^2); %标准值 plot(x,ya,x,y,':') %虚线代表Lagrange插值运算后的图像 function y=lagrange(x0,y0,x) ii=1:length(x0); y=zeros(size(x)); for i=ii ij=find(ii~=i); y1=1; for j=1:length(ij),y1=y1.*(x-x0(ij(j))); end y=y+y1*y0(i)/prod(x0(i)-x0(ij)); end end

运行结果：

二.二维插值

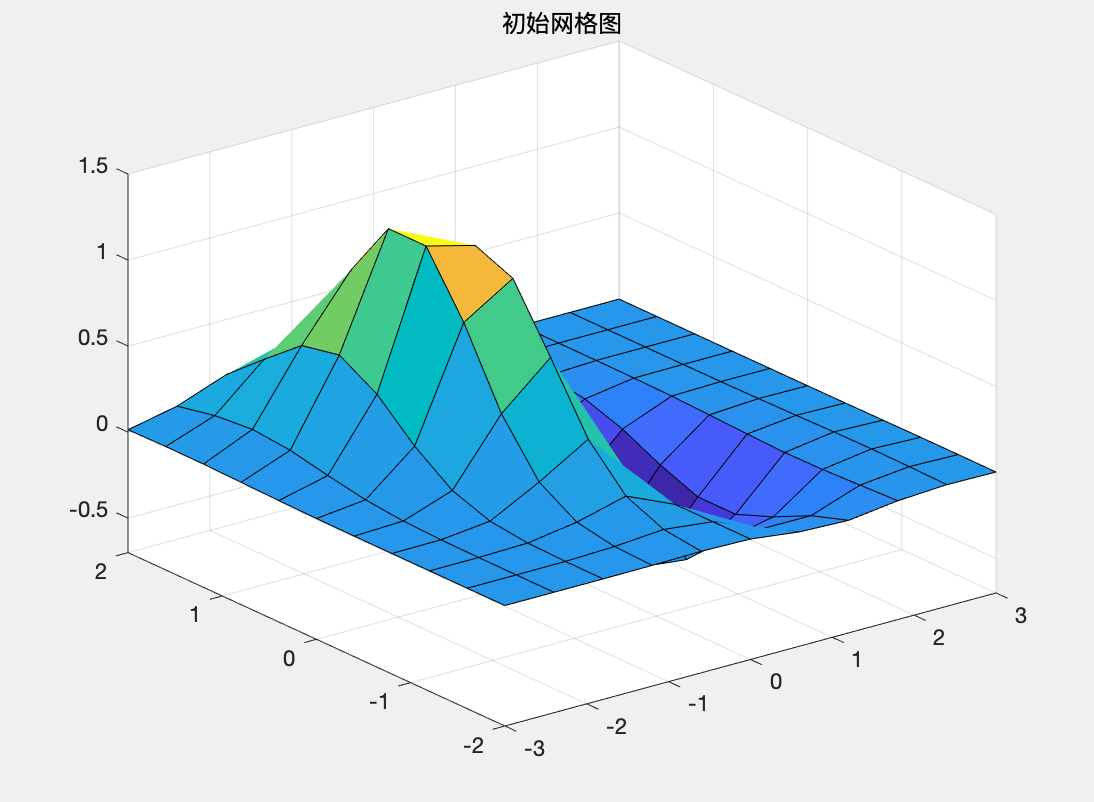
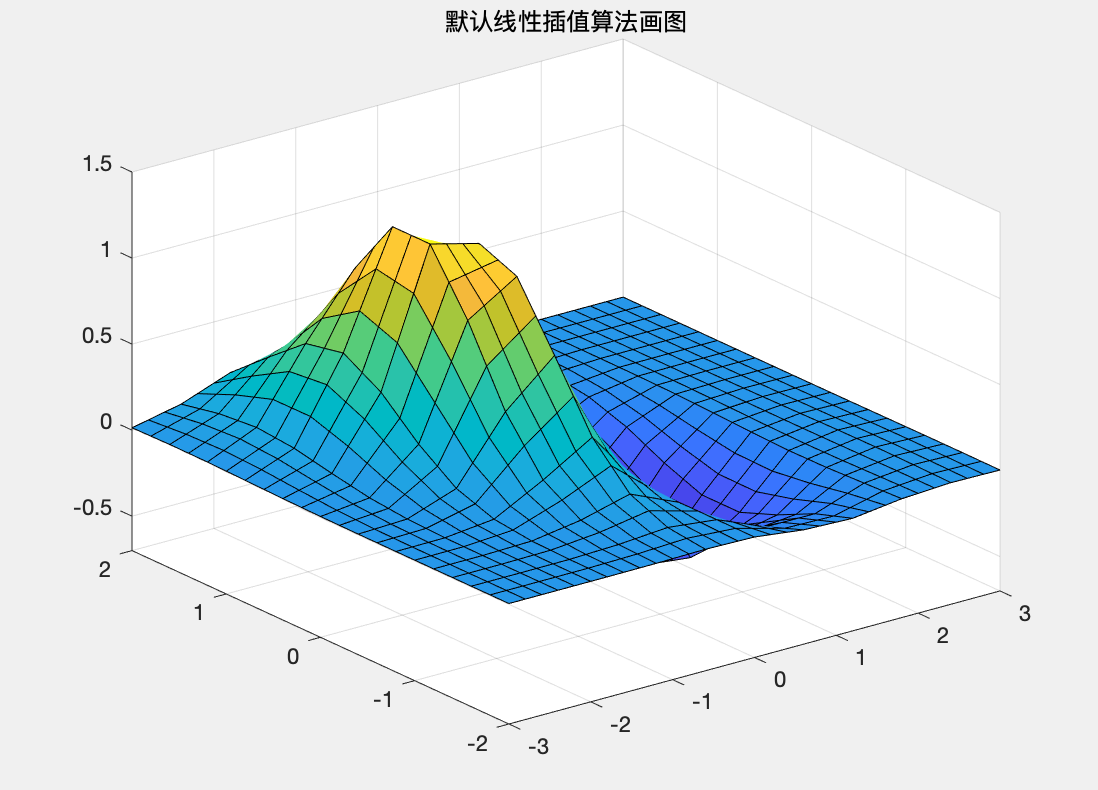
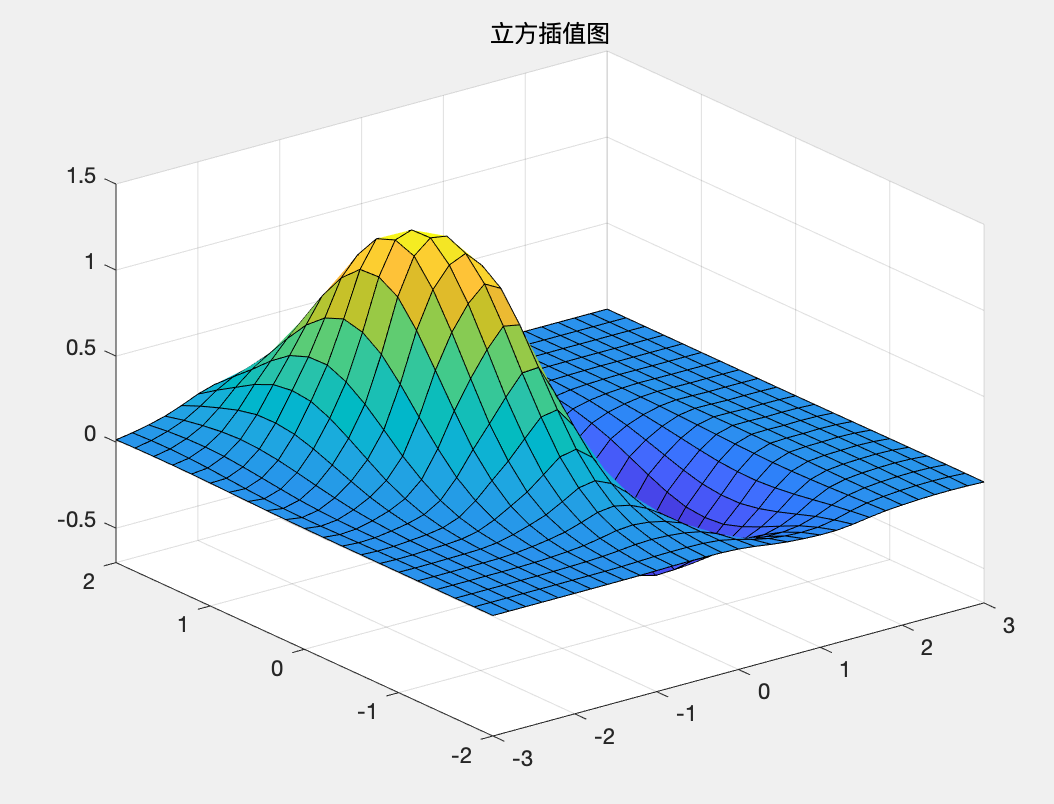
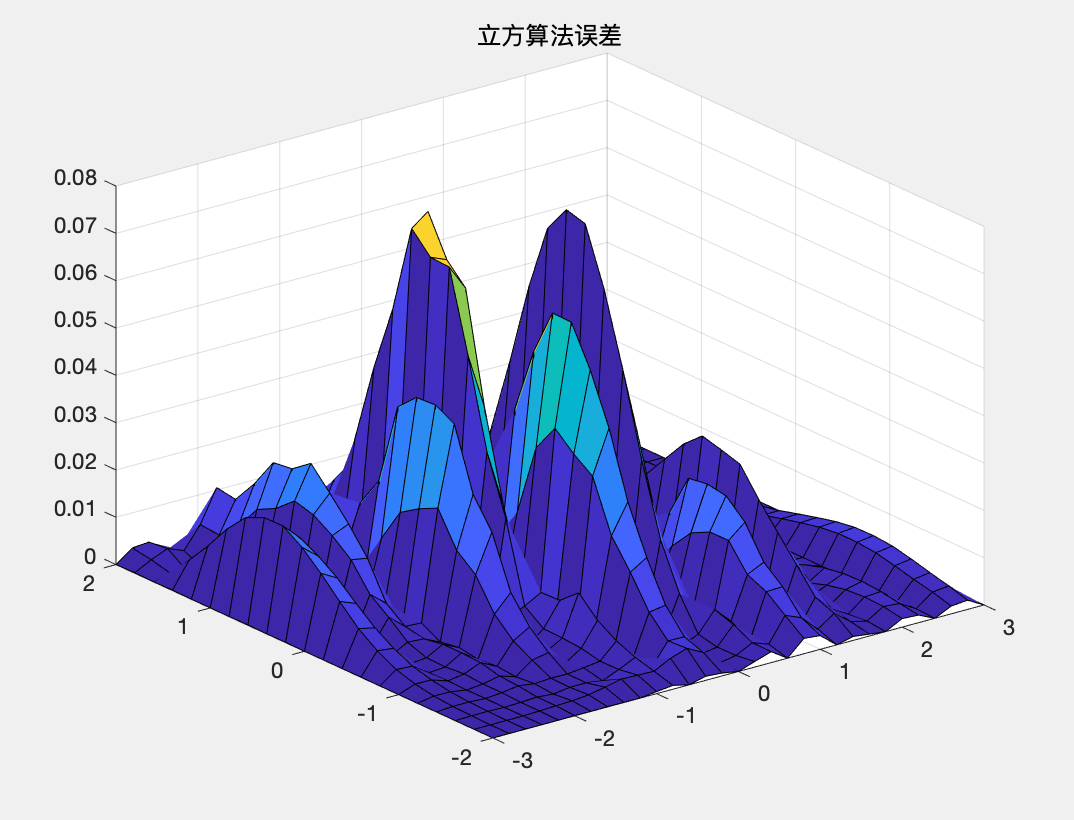
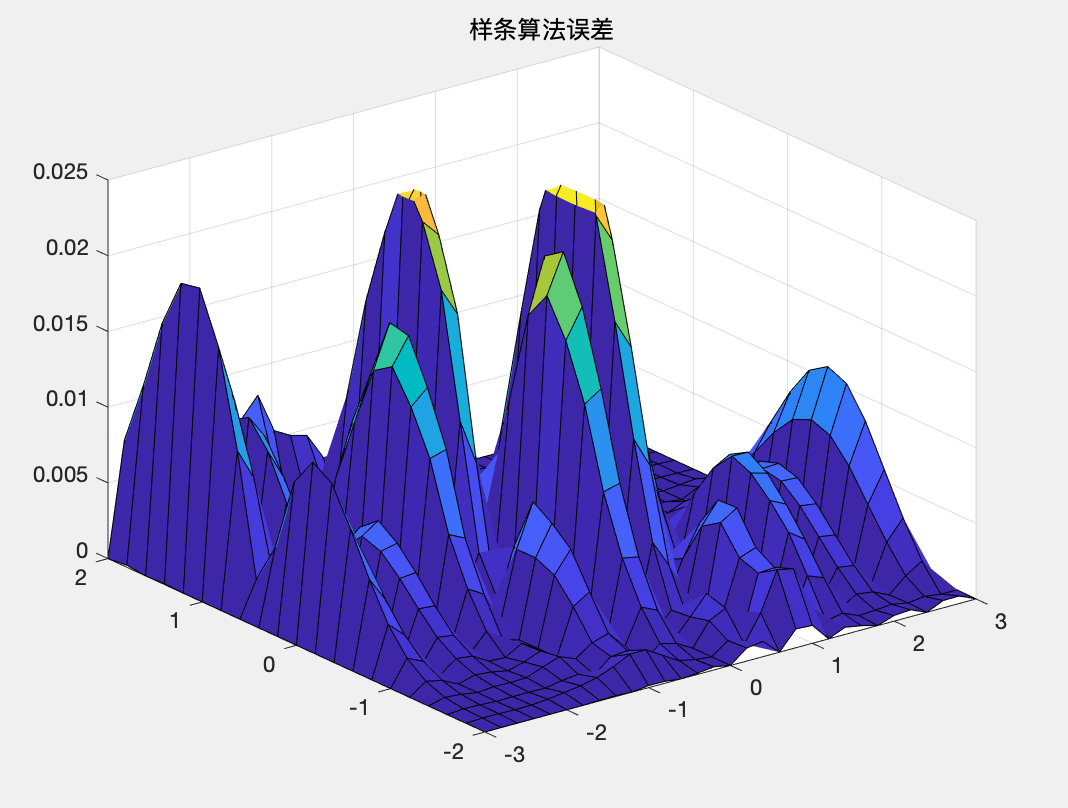
interp2命令作为二维数据内的插值运算，一共有三种常用的调用格式

格式1

ZI=interp2(X,Y,Z,XI,YI)

返回矩阵ZI，参量X和Y必须是单调的，且具有相同的划分格式，类似由命令meshgrid生成的一样。如果XI和YI中有在X与Y范围之外的点，那么就会返回NaN。

格式2

ZI=interp2(Z,XI,YI)

缺省的表示形式，X=1:n,Y=1:m，且[m,n]=size(Z)。具体计算类似格式1

格式3

ZI=interp2(X,Y,Z,XI,YI,method)

method表明用指定的算法计算二维插值。常用的算法有以下四种：

'linear'：双线性插值算法，一种缺省算法'nearest'：最临近插值'spline'：三次样条插值'cubic'：双三次插值例题3

由z=f(x,y)可计算出一些较稀疏的网格数据，尝试对整个函数曲面进行插值拟合，并比较拟合结果。

$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

解：

MATLAB代码如下：

clc;clear; %绘制已知数据的网格图 [x,y]=meshgrid(-3:.6:3,-2:.4:2); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); surf(x,y,z), axis([-3,3,-2,2,-0.7,1.5]) title('初始网格图'); %选择较密的插值点，用默认的线性插值算法进行插值 [x1,y1]=meshgrid(-3:.2:3,-2:.2:2); z1=interp2(x,y,z,x1,y1); figure; surf(x1,y1,z1),axis([-3,3,-2,2,-0.7,1.5]) title('默认线性插值算法画图'); %立方和样条插值 z2=interp2(x,y,z,x1,y1,'cubic'); z3=interp2(x,y,z,x1,y1,'spline'); figure; surf(x1,y1,z2),axis([-3,3,-2,2,-0.7,1.5]) title('立方插值图'); figure; surf(x1,y1,z3),axis([-3,3,-2,2,-0.7,1.5]) title('样条插值图'); %比较立方和样条插值算法误差 z_normal=(x1.^2-2*x1).*exp(-x1.^2-y1.^2-x1.*y1); figure; surf(x1,y1,abs(z_normal-z2)),axis([-3,3,-2,2,0,0.08]); title('立方算法误差'); figure; surf(x1,y1,abs(z_normal-z3)),axis([-3,3,-2,2,0,0.025]) title('样条算法误差');

运行结果：

三. 二维一般分布数据的插值

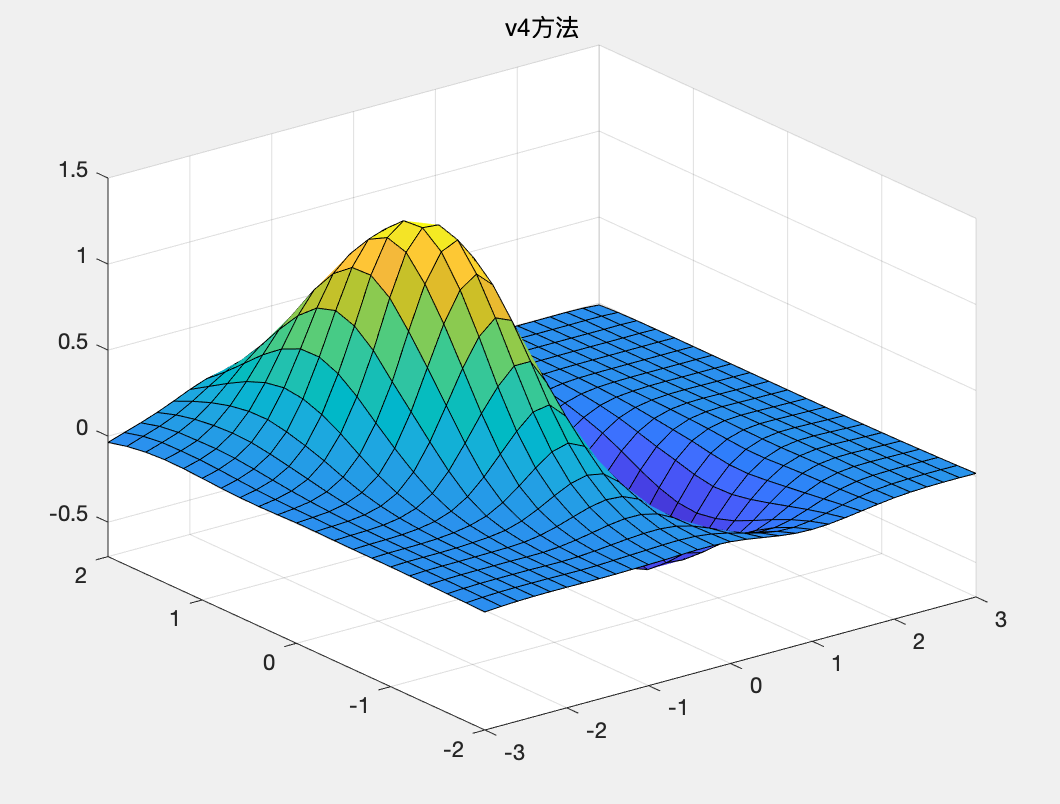
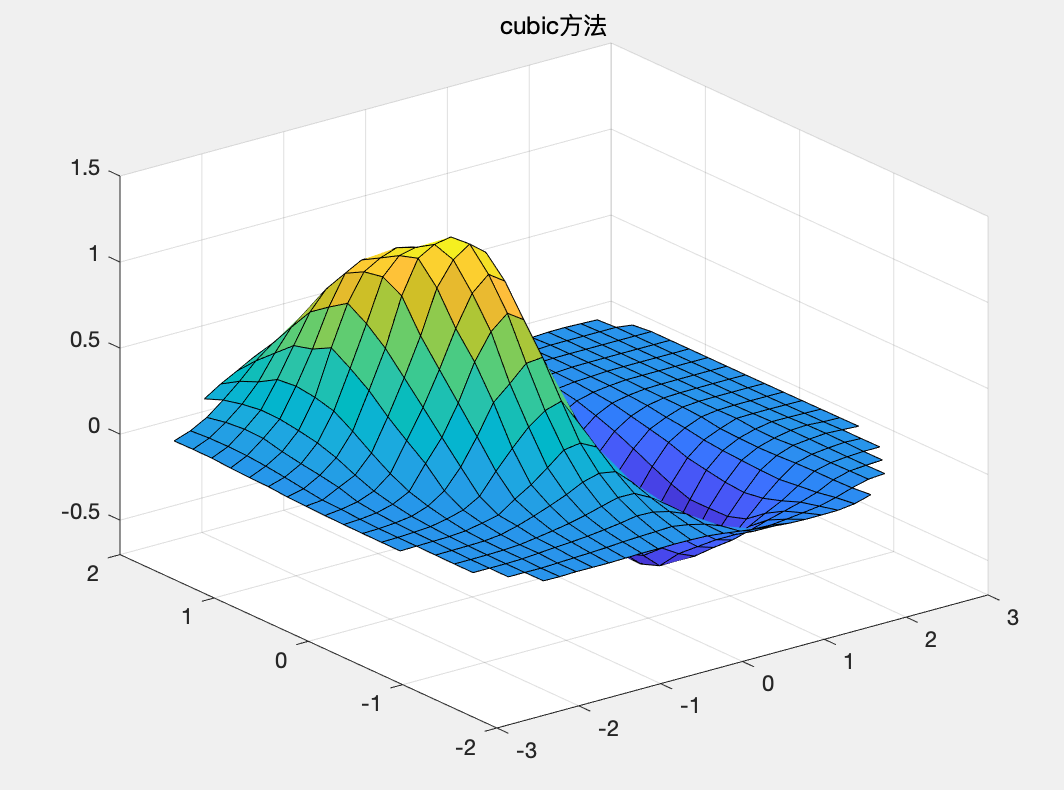
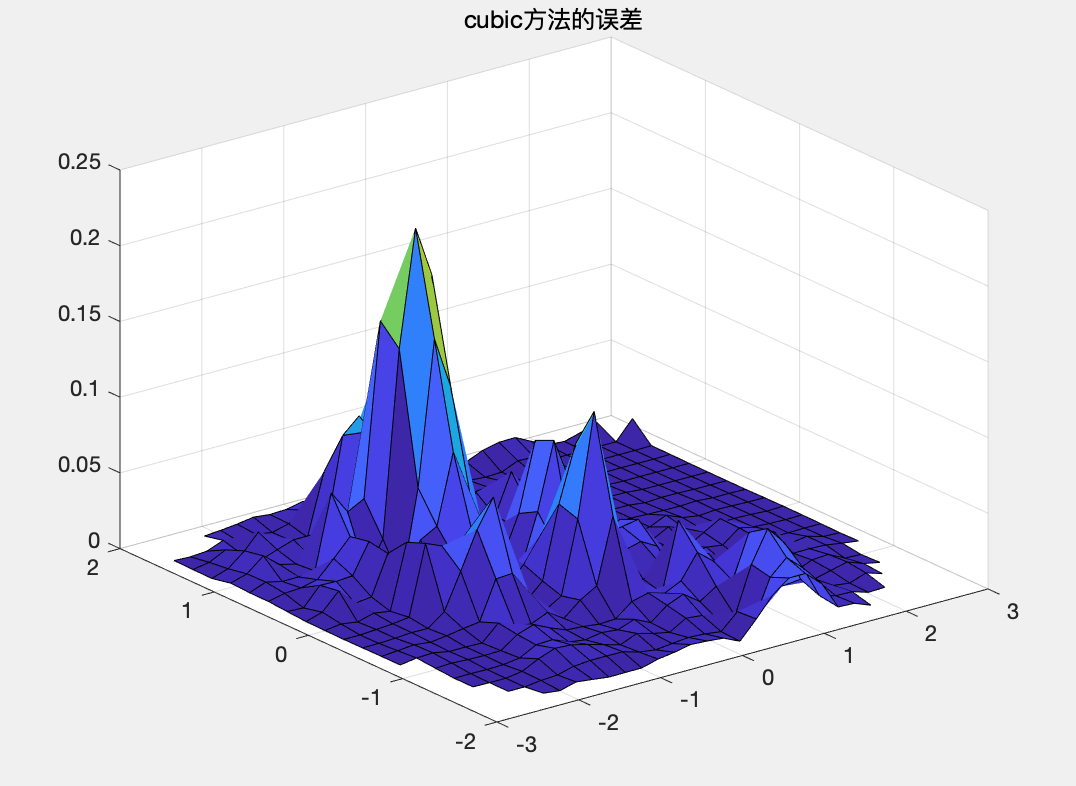
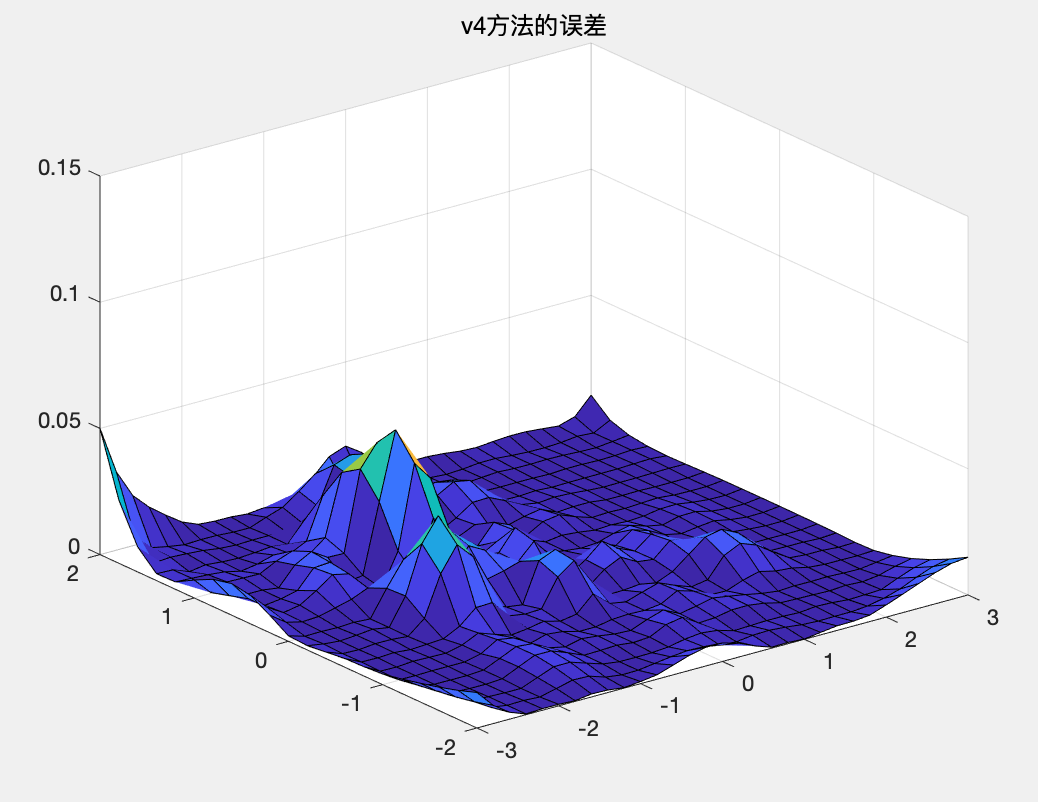
MATLAB中含有可对非网格数据进行插值的函数，调用的函数如下：

z=griddata(x0,y0,z0,x,y,'method')

上述中的method算法主要有五种，如下：

'v4'：MATLAB内含的插值算法，公认效果比较好'linear'：双线性插值算法，属于缺省算法'nearest'：最临近插值'spline'：三次样条插值'cubic'：双三次插值例题4

在x为[-3,3]，y为[-2,2]的矩形区域内随机选择一组坐标，用'v4'和'cubic'插值法进行处理，并对误差进行比较。

$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

解：

MATLAB代码如下：

clc;clear; x=-3+6*rand(200,1); y=-2+4*rand(200,1); %产生随机数 z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); [x1,y1]=meshgrid(-3:.2:3,-2:.2:2); %cubic方法 z1=griddata(x,y,z,x1,y1,'cubic'); surf(x1,y1,z1),axis([-3,3,-2,2,-0.7,1.5]) title('cubic方法'); %v4方法 z2=griddata(x,y,z,x1,y1,'v4'); figure; surf(x1,y1,z2),axis([-3,3,-2,2,-0.7,1.5]) title('v4方法'); %误差分析 z0=(x1.^2-2*x1).*exp(-x1.^2-y1.^2-x1.*y1); figure; surf(x1,y1,abs(z0-z1)),axis([-3,3,-2,2,0,0.25]) title('cubic方法的误差'); figure; surf(x1,y1,abs(z0-z2)),axis([-3,3,-2,2,0,0.15]) title('v4方法的误差');

运行结果：

例题5

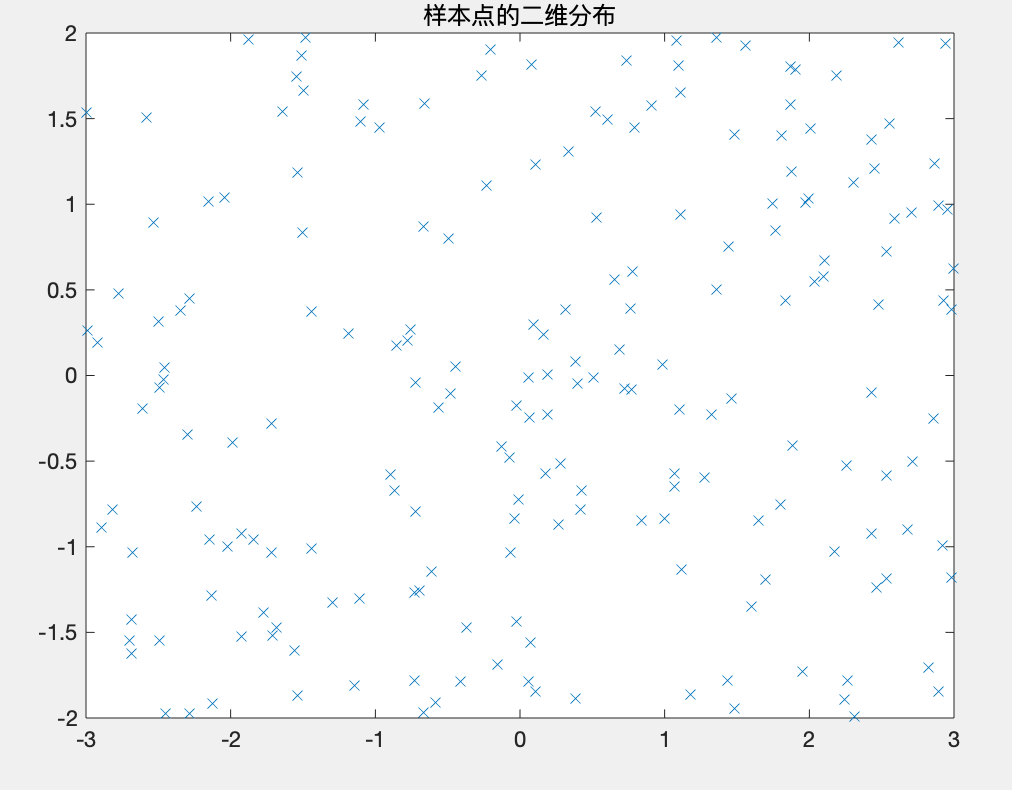
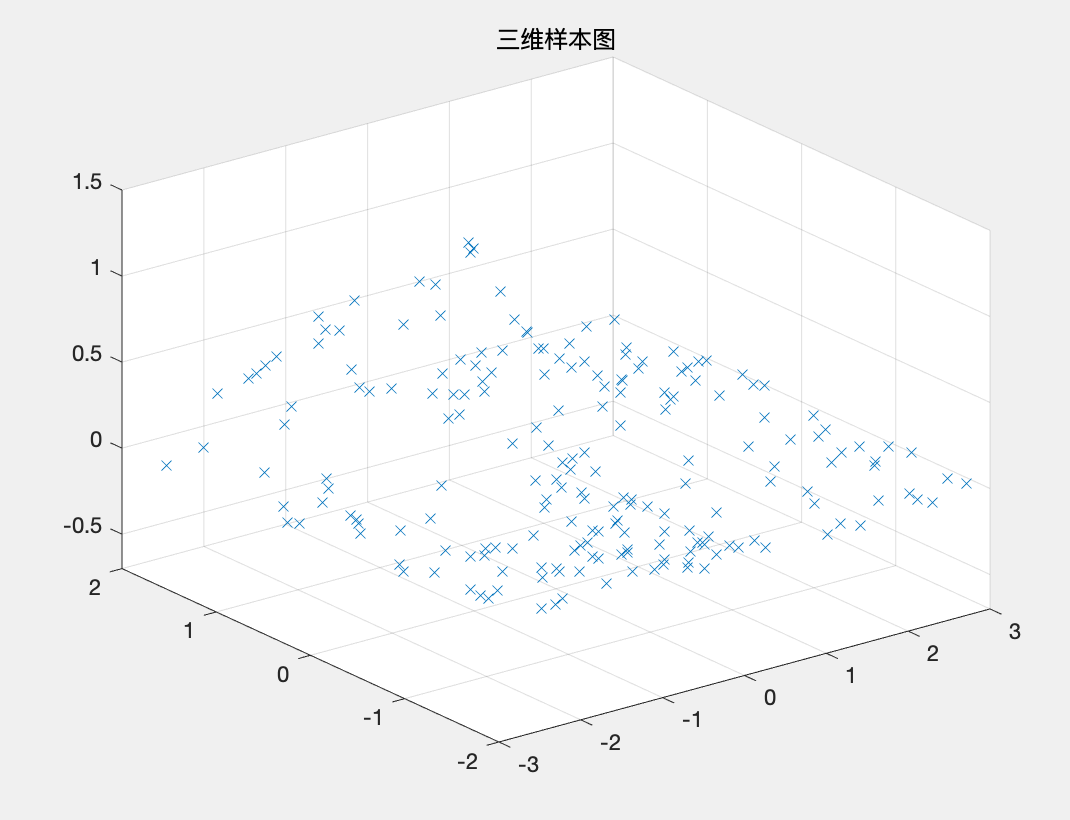
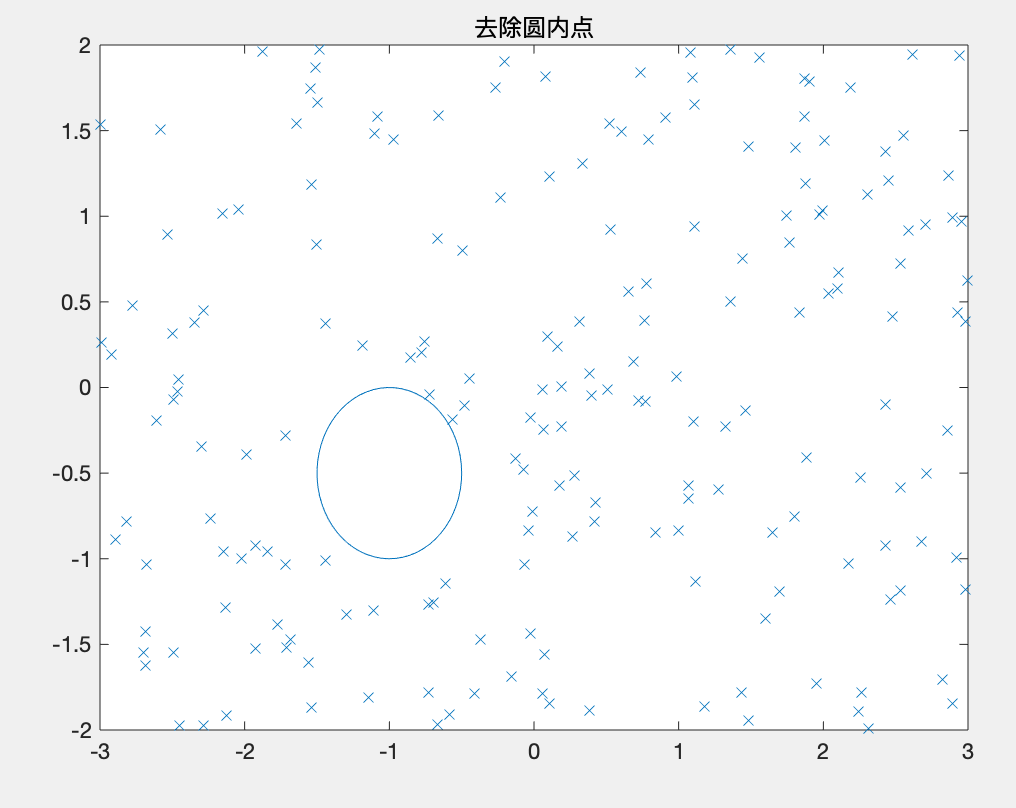
在x为[-3,3]，y为[-2,2]的矩形区域随机选择一组坐标中，对分布不均匀的数据，进行插值分析。

$z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}$

解：

本题我将MATLAB代码分成两部分。

（1）样本点数据处理的MATLAB代码如下：

clc;clear; x=-3+6*rand(200,1); y=-2+4*rand(200,1); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); %生成已知数据 plot(x,y,'x') %样本点的二维分布 title('样本点的二维分布'); figure; plot3(x,y,z,'x'),axis([-3,3,-2,2,-0.7,1.5]),grid %三维图 title('三维样本图'); %去除在(-1,-1/2)点为圆心，以0.5为半径的圆内的点 ii=find((x+1).^2+(y+0.5).^2>0.5^2); %找出满足条件的点坐标 x=x(ii);y=y(ii);z=z(ii); figure; plot(x,y,'x') t=[0:.1:2*pi,2*pi]; x0=-1+0.5*cos(t); y0=-0.5+0.5*sin(t); line(x0,y0) %在图形上叠加该圆，观察圆内样本点是否被去除 title('去除圆内点');

运行结果：

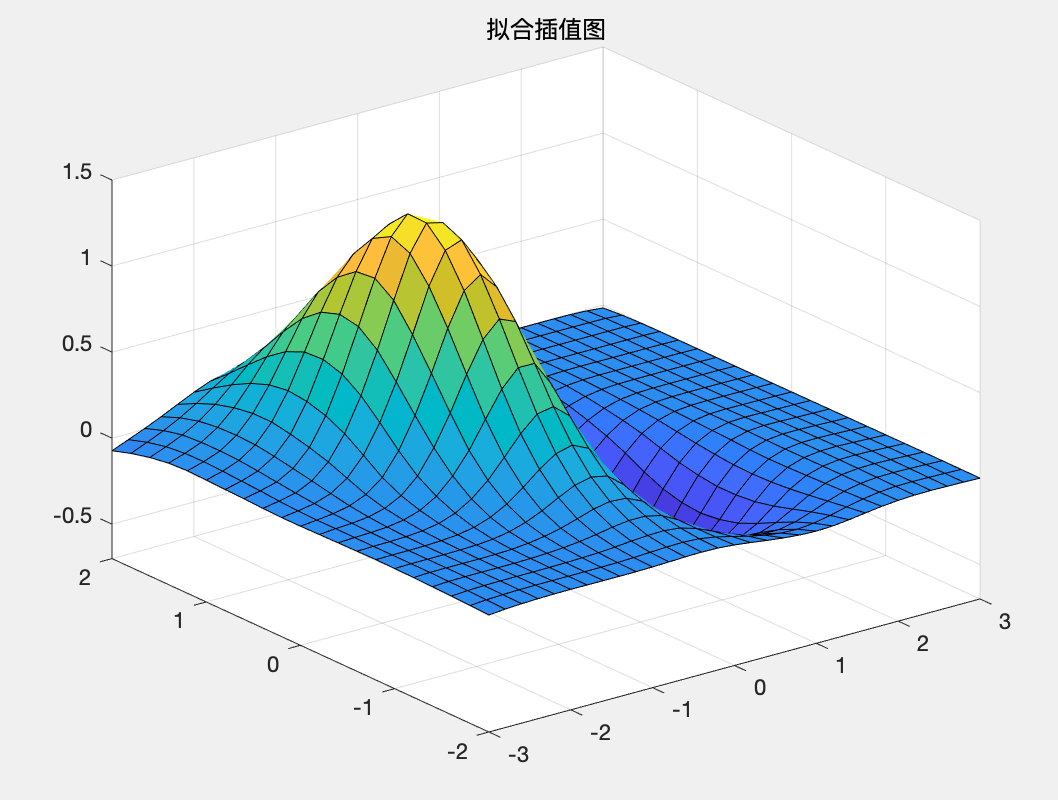
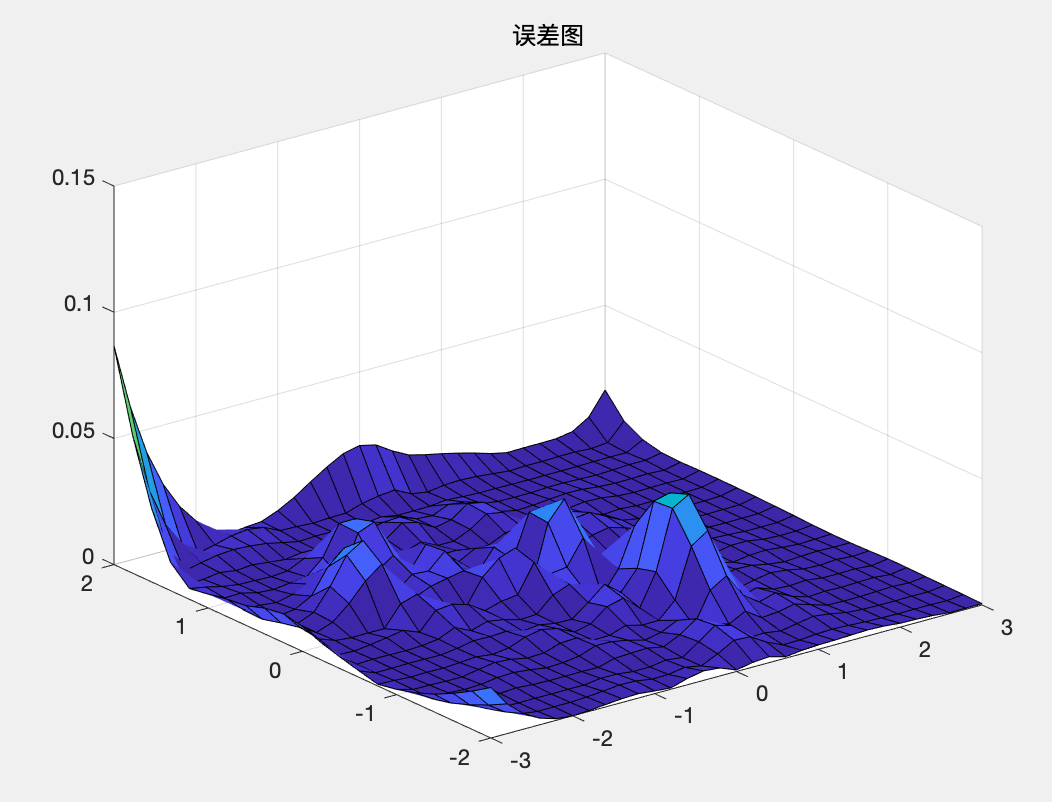
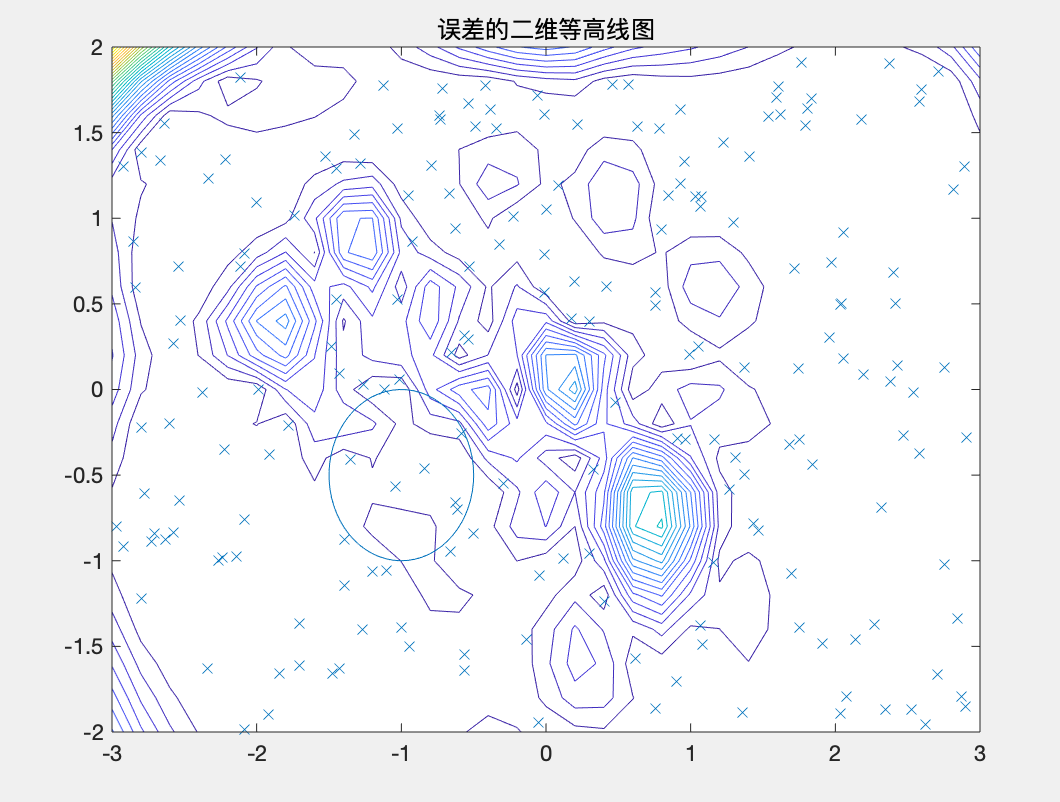
（2）插值与误差分析

MATLAB代码如下：

clc;clear; x=-3+6*rand(200,1); y=-2+4*rand(200,1); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); %生成已知数据 t=[0:.1:2*pi,2*pi]; x0=-1+0.5*cos(t); y0=-0.5+0.5*sin(t); %用新样本拟合出曲面 [x1,y1]=meshgrid(-3:.2:3,-2:.2:2); z1=griddata(x,y,z,x1,y1,'v4'); surf(x1,y1,z1),axis([-3,3,-2,2,-0.7,1.5]) title('拟合插值图'); %误差分析 z0=(x1.^2-2*x1).*exp(-x1.^2-y1.^2-x1.*y1); figure; surf(x1,y1,abs(z0-z1)),axis([-3,3,-2,2,0,0.15]) title('误差图'); figure; contour(x1,y1,abs(z0-z1),30); hold on,plot(x,y,'x'); line(x0,y0) %误差的二维等高线图 title('误差的二维等高线图');

运行结果：

【本文地址】

基于MATLAB的二维与三维插值拟合运算（附完整代码）

基于MATLAB的二维与三维插值拟合运算（附完整代码）

今日新闻

推荐新闻