(四十三)参数法与非参数法(历史模拟法)计算VaR |
您所在的位置:网站首页 › var蒙特卡洛模拟法 › (四十三)参数法与非参数法(历史模拟法)计算VaR |
(四十三)参数法与非参数法(历史模拟法)计算VaR
|
参数法
正态VaR:假设资产组合的收益率服从正态分布,那么VaR也服从正态分布,VaR=-(μ-Z·σ)×P0,算出来的是loss,如果为负则为收益。μ为资产组合的期望收益率,用往年平均收益率替代;σ为组合收益率的波动率;Z=Φ-1( c )为正态分布的分位数(取正数);P0为组合的价值。证明如下: 注意如果要求%VaR,那么公式中就不用乘P。对数正态VaR的值会比正态VaR要小。 假定某一投资组合在2018年12月28日(最后一个交易日)的投资组合市值为1亿元,组合中配置的5种金融资产配置为:贵州茅台股票15%,交通银行股票20%,嘉实增强信用基金50%,华夏恒生ETF基金5%,博时标普500ETF基金10%。管理层要求计算持有期分别为1天和10天、置信水平为99%情况下的VaR,同时假定整个投资组合收益率是服从正态分布或对数正态分布。 data=pd.read_excel('C:/Users/lenovo/Desktop/投资组合.xlsx',index_col=0) data Out[7]: 贵州茅台 交通银行 嘉实增强信用基金 华夏恒生ETF 博时标普500ETF 日期 2015-01-05 202.52 7.05 1.071 1.0955 1.1205 2015-01-06 197.83 6.90 1.073 1.0860 1.1105 2015-01-07 192.94 6.76 1.074 1.0964 1.1239 2015-01-08 191.76 6.53 1.074 1.1042 1.1446 2015-01-09 190.31 6.50 1.075 1.1075 1.1346 ... ... ... ... ... 2018-12-24 568.00 5.61 1.285 1.4505 1.5116 2018-12-25 565.79 5.63 1.286 1.4488 1.5116 2018-12-26 560.08 5.68 1.286 1.4475 1.5814 2018-12-27 563.00 5.72 1.286 1.4393 1.5963 2018-12-28 590.01 5.79 1.287 1.4358 1.5885 R=np.log(data/data.shift(1)).dropna() w=np.array([0.15,0.2,0.5,0.05,0.1]) Rmean=R.mean();Rcov=R.cov() Rp=np.sum(R.mean()*w) volp=np.sqrt(w@[email protected]) print('投资组合的μ={:.6f},σ={:.6f}'.format(Rp,volp)) 投资组合的μ=0.000268,σ=0.006427 def VaR_norm(miu,sigma,x,P,n):#n参数为持有期,x为置信水平 import scipy.stats as st z=abs(st.norm.ppf(q=1-x))#标准正态分布中1-x的概率对应的分位点 return -(miu-z*sigma)*P*np.sqrt(n) def VaR_lognorm(miu,sigma,x,P,n): import scipy.stats as st z=abs(st.norm.ppf(q=1-x)) return (1-np.exp(miu-z*sigma))*P*np.sqrt(n) print('99%置信水平下1天的normal VaR为{:.2f},lognormal VaR为{:.2f}'.format(\ VaR_norm(Rp,volp,0.99,1e8,1),VaR_lognorm(Rp,volp,0.99,1e8,1))) 99%置信水平下1天的normal VaR为1468366.22,lognormal VaR为1457638.30 print('99%置信水平下10天的normal VaR为{:.2f},lognormal VaR为{:.2f}'.format(\ VaR_norm(Rp,volp,0.99,1e8,10),VaR_lognorm(Rp,volp,0.99,1e8,10))) 99%置信水平下10天的normal VaR为4643381.70,lognormal VaR为4609457.03以第二个结果为例,在99%的置信水平、持有期为10天的情况下,VaR达到了464.34万元,意味着从理论上来说未来的10个交易日内,有99%的把握认为1亿元的投资组合累计最大亏损不会超过464.34万元。 非参数法(历史模拟法)历史模拟法的思路是将所有样本的收益率或收益额进行排序,根据置信水平找出对应分位数的值(数值小的一端),再取绝对值就是VaR。依然以上述案例为例,用历史模拟法计算持有期分别为1天和10天、置信水平为99%情况下的VaR。 step1:生成投资组合的日收益序列: rp=pd.Series((1e8*R)@w,index=R.index)#投资组合的日收益额 import matplotlib.pyplot as plt from pylab import mpl mpl.rcParams['font.sans-serif']=['SimHei'] mpl.rcParams['axes.unicode_minus']=False plt.hist(rp,bins=40,edgecolor='k') plt.xlabel('投资组合日收益额') plt.ylabel('频数') plt.title('投资组合日收益额直方图') plt.grid()
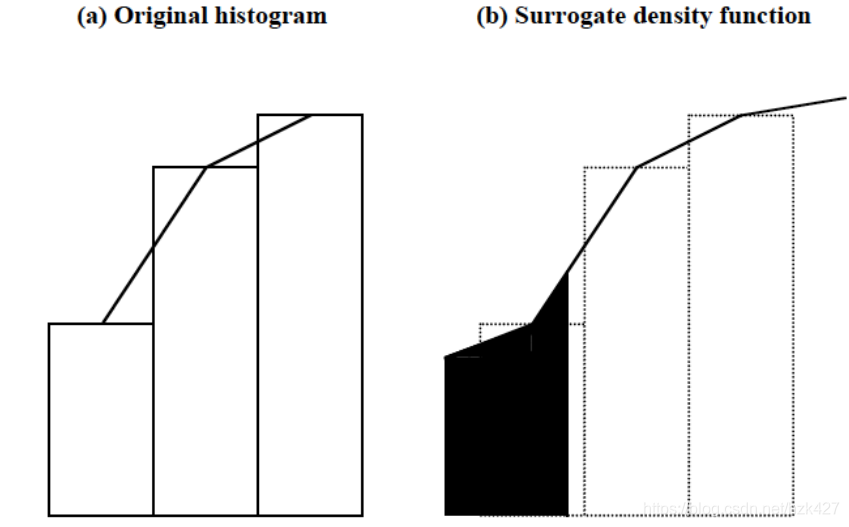
在99%的置信水平下历史模拟法计算出的10天VaR=675.38万元>正态VaR=464.34万元,可见在本案例中历史模拟法具有对尾部极端风险更强的捕捉能力。 还有一种改进的参数法叫非参数密度估计(Non-parametric Density Estimation),将损失额直方图的每一根立柱的顶部中点进行连线,那么在线下的区域就可以当做该分布的概率密度函数,这样我们就能根据求出任意置信水平下的VaR,可以解决传统历史模拟法下n个样本最多只能有n个置信水平的问题。 |
【本文地址】
今日新闻 |
推荐新闻 |
 对数正态VaR:假设资产组合的对数收益率服从正态分布,那么VaR服从对数正态分布,VaR=(1-eμ-Z·σ)×P0。可简单证明如下:受到冲击后的价格P=P0(eR),VaR=|P0-P|=|P0(1-eR)|,对数收益率R=ln(P/P0)服从正态分布,那么在此置信水平下的极端收益率为μ-z·σ,代入到R中即得VaR公式。
对数正态VaR:假设资产组合的对数收益率服从正态分布,那么VaR服从对数正态分布,VaR=(1-eμ-Z·σ)×P0。可简单证明如下:受到冲击后的价格P=P0(eR),VaR=|P0-P|=|P0(1-eR)|,对数收益率R=ln(P/P0)服从正态分布,那么在此置信水平下的极端收益率为μ-z·σ,代入到R中即得VaR公式。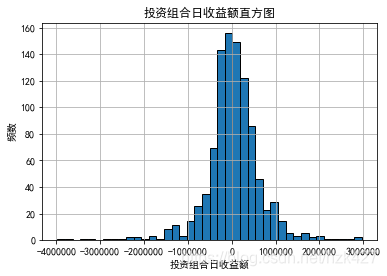 step2:对投资组合的日收益额序列进行正态性检验,计算投资组合的VaR:
step2:对投资组合的日收益额序列进行正态性检验,计算投资组合的VaR: