Sa函数 与 sinc函数 |
您所在的位置：网站首页 › sin周期公式图像 › Sa函数 与 sinc函数 |
Sa函数 与 sinc函数
|
文章目录
【 1. Sa函数】【 2. sinc函数 】【 3. 两者的关系 】【 4. 傅里叶变换分析 】4.1 矩形窗的傅里叶变换4.2 Sa 函数的傅里叶变换4.3 Sinc 函数的傅里叶变换4.4 Bsinc(Bt) 的傅里叶变换4.5
B
s
i
n
c
[
B
(
t
−
τ
m
)
]
Bsinc[B(t-τ_m)]
Bsinc[B(t−τm)] 的傅里叶变换
【 1. Sa函数】
S a ( x ) = sin ( x ) x Sa(x)=\frac{\sin(x)}{ x} Sa(x)=xsin(x) 也称为 抽样函数 。傅里叶变换 π [ u ( w + 1 ) − u ( w − 1 ) ] \pi [u(w+1)-u(w-1)] π[u(w+1)−u(w−1)]积分性质 ∫ 0 ∞ S a ( t ) d t = π 2 \int_{0}^{\infty}Sa\left(t\right)dt=\dfrac{\pi}{2} ∫0∞Sa(t)dt=2π， ∫ − ∞ + ∞ S a ( t ) d t = π \int_{-\infty}^{+\infty}S a\left(t\right)dt=\pi ∫−∞+∞Sa(t)dt=π是一个 偶函数 。 【 2. sinc函数 】s i n c ( x ) = sin ( π x ) π x sinc (x)=\frac{\sin(\pi x)}{\pi x} sinc(x)=πxsin(πx) 也称为 辛格函数 。傅里叶变换 u ( w + 1 π ) − u ( w − 1 π ) u(\frac{w+1}{\pi})-u(\frac{w-1}{\pi}) u(πw+1)−u(πw−1)
【 3. 两者的关系 】
s i n c ( x ) = S a ( π x ) sinc(x)=Sa(\pi x) sinc(x)=Sa(πx) 【 4. 傅里叶变换分析 】 4.1 矩形窗的傅里叶变换
s i n c ( t ) = sin ( π t ) π t sinc(t)=\frac{\sin(\pi t)}{\pi t} sinc(t)=πtsin(πt) F ( j ω ) = u ( w + 1 π ) − u ( w − 1 π ) = { 1 ∣ ω ∣ < 1 0 ∣ ω ∣ > 1 F(\text{j}\omega)=u(\frac{w+1}{\pi})-u(\frac{w-1}{\pi})=\begin{cases}{1}&{\left|\omega\right|1}\end{cases} F(jω)=u(πw+1)−u(πw−1)={10∣ω∣1 4.4 Bsinc(Bt) 的傅里叶变换 傅里叶变换的尺度变换性质： f ( a t ) ⇌ 1 ∣ a ∣ F ( j w a ) f(at)\xrightleftharpoons[]{} \frac{1}{|a|}F(j\frac{w}{a}) f(at) ∣a∣1F(jaw) B s i n c ( B t ) = B sin ( π B t ) π B t = sin ( π B t ) π t Bsinc(Bt)=B \frac{\sin(\pi Bt)}{\pi Bt}=\frac{\sin(\pi Bt)}{\pi t} Bsinc(Bt)=BπBtsin(πBt)=πtsin(πBt) F ( j w ) = r e c t ( f B ) = { 1 ∣ f ∣ < B 2 0 ∣ f ∣ > B 2 F(jw)=\mathrm{rect}\Big(\frac{f}{B}\Big)=\begin{cases}{1}&{\left|f\right|\frac{B}{2}}\end{cases} F(jw)=rect(Bf)={10∣f∣2B 4.5 B s i n c [ B ( t − τ m ) ] Bsinc[B(t-τ_m)] Bsinc[B(t−τm)] 的傅里叶变换 雷达回波基带信号脉压匹配滤波器的输出一般为 r p c ( t ^ , t m ) = B s i n c [ B ( t − τ m ) ] ⋅ e x p ( − j 2 π f 0 τ m ) r_{pc}(\widehat{t},t_m)=Bsinc[B(t-τ_m)]·exp(-j2\pi f_0 \tau _m) rpc(t ,tm)=Bsinc[B(t−τm)]⋅exp(−j2πf0τm)，故对其包络 B s i n c [ B ( t − τ m ) ] Bsinc[B(t-τ_m)] Bsinc[B(t−τm)] 的傅里叶变换分析非常必要。傅里叶变换的时移性质： f ( t ± t 0 ) ⇌ e ± j w t 0 F ( j w ) f(t±t_0)\xrightleftharpoons[]{} e^{±jwt_0}F(jw) f(t±t0) e±jwt0F(jw) B s i n c [ B ( t − τ m ) ] Bsinc[B(t-τ_m)] Bsinc[B(t−τm)] F ( j w ) = e − j w τ m r e c t ( f B ) F(jw)=e^{-jw\tau_m} \mathrm{rect}\Big(\frac{f}{B}\Big) F(jw)=e−jwτmrect(Bf) |
g
τ
(
t
)
=
r
e
c
t
(
t
)
=
{
1
,
∣
t
∣
<
τ
2
0
,
∣
t
∣
>
τ
2
g_\tau(t)=rect(t)=\begin{cases}1,&\mid t\mid\dfrac\tau2\end{cases}
gτ(t)=rect(t)=⎩
⎨
⎧1,0,∣t∣2τ
F
(
j
ω
)
=
∫
−
τ
/
2
τ
/
2
e
−
j
ω
t
d
t
=
e
−
j
ω
τ
2
−
e
j
ω
τ
2
−
j
ω
=
sin
(
ω
τ
2
)
w
2
=
τ
S
a
(
ω
τ
2
)
F(\text{j}\omega)=\int_{-\tau/2}^{\tau/2}\mathrm{e}^{-j\omega t}\mathrm{d}t=\frac{\mathrm{e}^{-j\omega\frac{\tau}{2}}-\mathrm{e}^{j\omega\frac{\tau}{2}}}{-j\omega}=\frac{\sin(\frac{\omega \tau}{2})}{\frac{w}{2}}=\tau Sa(\frac{\omega \tau}{2})
F(jω)=∫−τ/2τ/2e−jωtdt=−jωe−jω2τ−ejω2τ=2wsin(2ωτ)=τSa(2ωτ)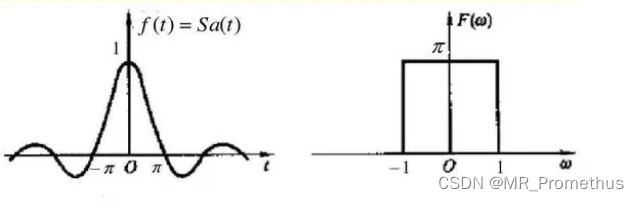
S
a
(
t
)
=
s
i
n
t
t
Sa(t)=\frac{sint}{t}
Sa(t)=tsint
F
(
j
ω
)
=
π
[
u
(
w
+
1
)
−
u
(
w
−
1
)
]
=
{
π
∣
ω
∣
<
1
0
∣
ω
∣
>
1
F(\text{j}\omega)=\pi [u(w+1)-u(w-1)]=\begin{cases}{\pi}&{\left|\omega\right|1}\end{cases}
F(jω)=π[u(w+1)−u(w−1)]={π0∣ω∣1【本文地址】