有限差分法（Finite Difference Method，FDM）是一种求解微分方程数值解的近似方法，其主要原理是对微分方程中的微分项进行直接差分近似，从而将微分方程转化为代数方程组求解。有限差分法的原理简单，粗暴有效，最早由远古数学大神欧拉（L. Euler 1707-1783）提出，他在1768年给出了一维问题的差分格式。1908年，龙格（C. Runge 1856-1927）将差分法扩展到了二维问题【对，就是龙格-库塔法中的那个龙格】。但是在那个年代，将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题，因此并未得到大量的应用。随着计算机技术的发展，快速准确地求解庞大的代数方程组成为可能，因此逐渐得到大量的应用。发展至今，有限差分法已成为一个重要的数值求解方法，在工程领域有着广泛的应用背景。本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述，给出其基本的应用方法，对于一些深入的问题不做讨论。

首先，有限差分法是一种求解微分方程的数值方法，其面对的对象是微分方程，包括常微分方程和偏微分方程。此外，有限差分法需要对微分进行近似，这里的近似采取的是离散近似，使用某一点周围点的函数值近似表示该点的微分。下面将对该方法进行概述。

这里我们使用一个简单的例子来简述有限差分法的基本原理，考虑如下常微分方程

\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\ u(x=a) = d \end{cases} \tag{1}

微分方程与代数方程最大的不同就是其包含微分项，这也是求解微分方程最难处理的地方。有限差分法的基本原理即使用近似方法处理微分方程中的微分项。为了得到微分的近似，我们最容易想到的即导数定义

u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x} \approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}

上式后面的近似表示使用割线斜率近似替代切线斜率，\Delta x​ 即为步长，如图 1(a)所示。式(2)表明函数在某一点的微分可以由相邻点的函数值近似确定。显然，这里微分近似的精度与步长的选取有关，步长越短则越精确。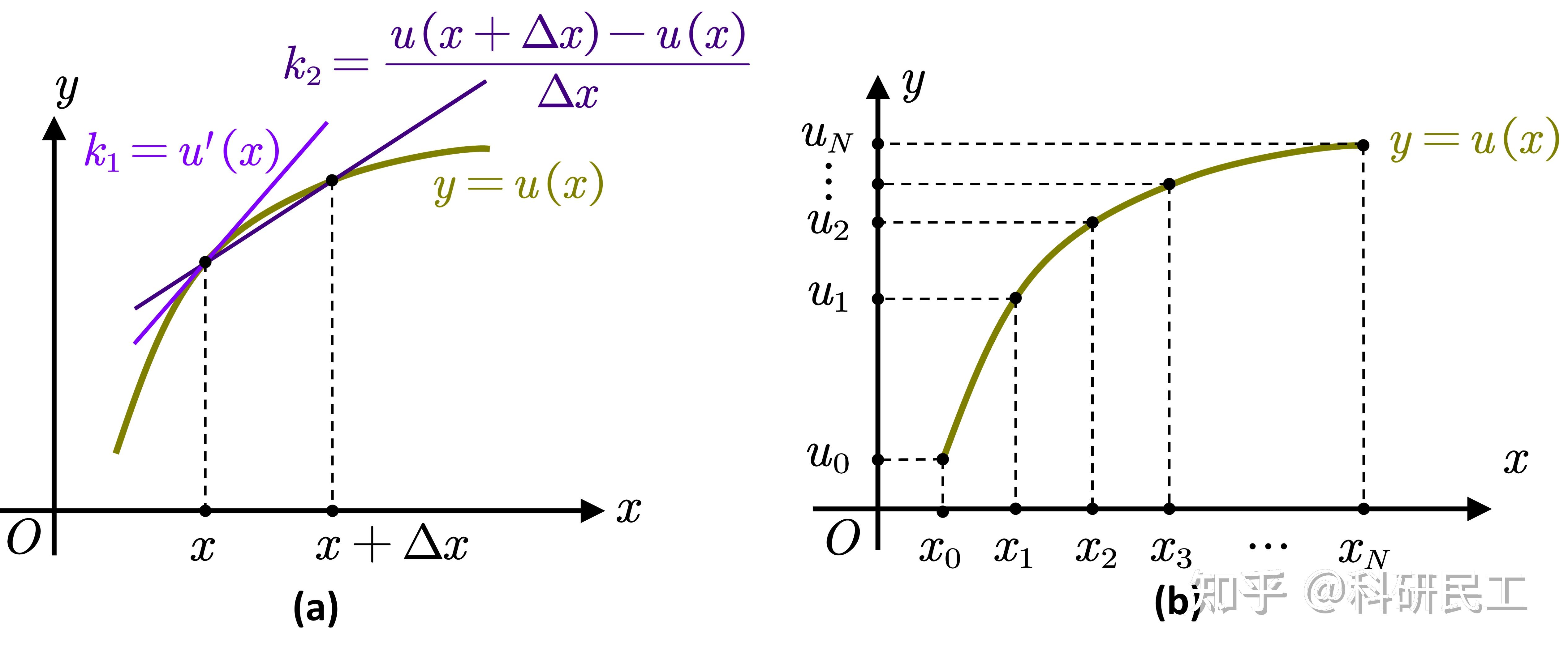

因此，这里首先需要对求解域进行离散，然后分别得到各离散点上的微分近似。对于示例的一维问题，将求解区间等分为 N 个区间，步长为 h，分别将包含首尾的各结点记为 x_0, x_1, x_2, ..., x_N，对应的函数值为 u_0, u_1, u_2, ..., u_N，对应各点的一阶微分记为 u'_0, u'_1, u'_2, ..., u'_N​，如图 1(b) 所示。这样，就把原问题的求解转化为了各结点函数值 u_i​ 的求解。式(2)的离散形式表示为

u_i'=\frac{1}{h}(u_{i+1}-u_i), \quad i=0,1,2,...,N-1 \tag{3}

将式（3）代入方程（1）可以得到

\begin{cases} (u_{i+1}-u_i)/h+c(x_i)u_i=f(x_i) \\ u_0 = d \end{cases}; \quad\quad i=1,2,...,N-1 \tag{4}

这里的结点坐标 x_i = a + ih, \; (i=0,1,2,3,4)，步长 h=(b-a)/N 均为已知。记 c_i=c(x_i), f_i=f(x_i)， 将式(4)合并同类项可以得到如下递推关系

u_{i+1} = (1-hc_i)u_i+hf_i; \; u_0 = d, \; i=0,1,2,3,...,N-1 \tag{5}

上式共有 N​​ 个方程（i=0,1,2,...,N-1​​），包括 N​​ 个未知数（u_1, u_2, ..., u_N​​​​​​​），刚好可以求解得到各结点上的待求函数的值，从而得到原问题在求解域上的近似解。由于该问题中初值已给定，按照各结点依次迭代就可以得到该问题的解。此外，为了给出更一般化的求解方法，可以将(5)写成矩阵的形式，即

\mathbf{A} \mathbf{u} = \mathbf{F} \tag{6}

即

\left[ \begin{matrix} 1 & \\ C_1& 1 \\ & \ddots& \ddots \\ & & C_{N-1}& 1 \\ \end{matrix} \right] \left\{ \begin{array}{c} u_1 \\ u_2 \\ \vdots \\ u_N \\ \end{array} \right\} = \left\{ \begin{array}{c} F_0 \\ F_1 \\ \vdots \\ F_{N-1} \\ \end{array} \right\} - \left\{ \begin{array}{c} C_0 u_0 \\ 0 \\ \vdots \\ 0 \\ \end{array} \right\} \tag{7}

其中 \mathbf{u} = \left\{u_1, \, \dots, \, u_{N-1}, \, u_{N} \right\}^{\mathrm{T}} 总共包含 N 个待求结点值。C_i = hc_i - 1，F_i = hf_i 。上述方程组的系数矩阵 \mathbf{A} 显然可逆，则上述问题的解总是可以表示为 \mathbf{u}= \mathbf{A}^{-1} \mathbf{F}。为了验证上述结果的正确性，我们取 c(x)=1, f(x)=\sin(x) + \cos(x), 求解区间为 x \in [0,2 \pi]，且满足边界条件 u(0)=0，则原问题(1)可以写为如下形式

\begin{cases} u'(x) + u(x) = \sin(x) + \cos(x), \quad x \in [0, 2 \pi]; \\ u(x=0) = 0 \end{cases} \tag{8}

则该问题对应方程组(6)中的 C_i=h-1​​，F_i=h[\sin(x_i) + \cos(x_i)]​​，d=0​​。将上述表达式代入式(7)并利用 \mathbf{u}= \mathbf{A}^{-1} \mathbf{F}​​ 即可以得到该问题的近似解。此外，上述方程的解析解可以容易给出为 u(x)=\sin(x)​​​​​。分别取 N=5,10,20,100​​​ 时有限差分法结果与解析解对比如图(2)所示，可以看到网格划分越精细