【预测模型】基于人工鱼群算法优化BP神经网络实现数据预测matlab源码

您所在的位置：网站首页 › narx神经网络和bp神经网络 › 【预测模型】基于人工鱼群算法优化BP神经网络实现数据预测matlab源码

【预测模型】基于人工鱼群算法优化BP神经网络实现数据预测matlab源码

2023-11-29 00:46| 来源: 网络整理| 查看: 265

1 算法介绍

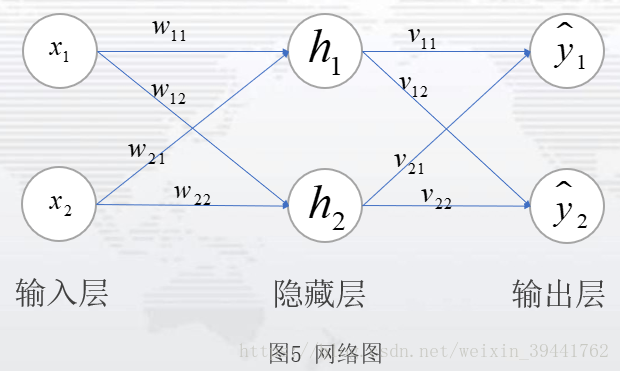
1.1 BP神经网络

1、反向传播算法应用领域

反向传播算法应用较为广泛，从字面意思理解，与前向传播相互对应。在简单的神经网络中，反向传播算法，可以理解为最优化损失函数过程，求解每个参与运算的参数的梯度的方法。在前馈神经网络中，反向传播从求解损失函数偏导过程中，步步向前求解每一层的参数梯度。在卷积神经网络中，反向传播可以求解全连接层的参数梯度。在循环神经网络中，反向传播算法可以求解每一个时刻t或者状态t的参数梯度（在RNN\LSTM\GRU中，反向传播更多是BPTT）。笔者如今对于BP的理解，认为是在优化损失函数或者目标函数过程中，求解参与运算的参数的梯度方法，是一种比较普遍的说法。

2、准备知识--反向传播(BP)算法应用于神经网络

反向传播(BP)算法在深度学习中，应用广泛。这里仅以前馈神经网络中的BP算法作为介绍。神经网络是一个由输入层、隐藏层、输出层三部分组成的网络，如图(1)：数据从输入层，经过权重值和偏置项的线性变换处理，再通过激活层，得到隐藏层的输出，也即下一层的输入；隐藏层到输出层之间是，经过权重值和偏置项的线性变换，之后通过激活层，得到输出层。

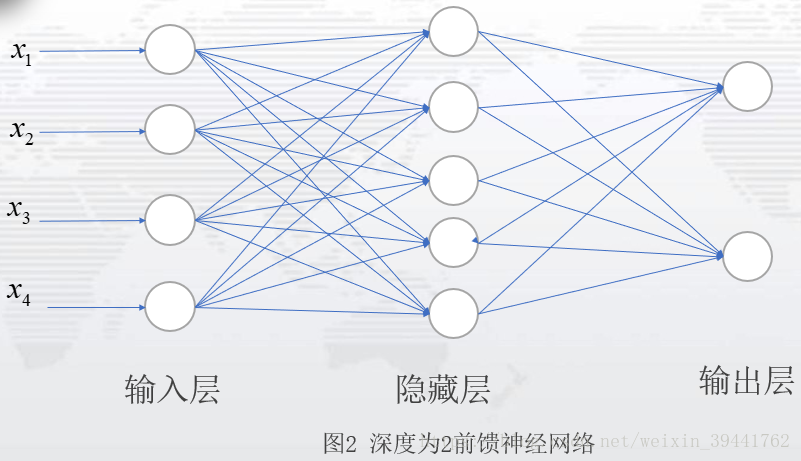
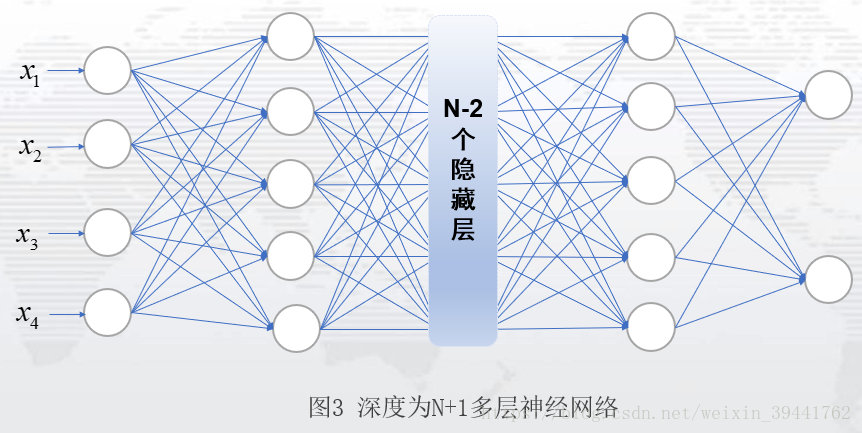
图2表示一个网络层为2的前馈神经网络：一个隐藏层，一个输出层；隐藏单元为5，记输入层到隐藏层的权重值为W，偏置项为b1,激活函数为g1，隐藏层到输出层的权重值为V,偏置项为b2，激活函数为g2，则图2的模型即为：

$\hat{Y}=g_{2}(V^{T}g_{1}(W^{T}X+b_{1})+b_{2})$

图2是一个比较简单的神经网络，通常，我们见到的神经网络，是具有多个隐藏层的网络，如图3：这是一个隐藏层个数为N个，每层隐藏单元数为5的神经网络。（PS：隐藏层设计，可以考虑层数设计和隐藏单元设计，可根据自己的需要自行设计。)

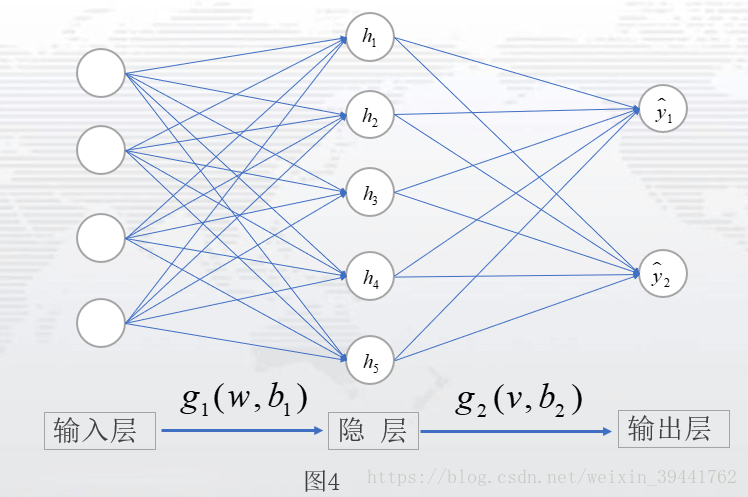
从输入层到隐藏层再到输出层，这一向前传递的过程，我们称之为前向传播。前向传播过程，往往是我们设定模型的过程，也可以理解为设定数学表达式或者列方程的过程。

3、BP算法原理及其实施步骤

BP算法的核心思想：使用梯度下降来搜索可能的权向量的假设空间，以找到最佳的拟合样例的权向量。具体而言，即利用损失函数，每次向损失函数负梯度方向移动，直到损失函数取得最小值。

或者说，反向传播算法，是根据损失函数，求出损失函数关于每一层的权值及偏置项的偏导数，也称为梯度，用该值更新初始的权值和偏置项，一直更新到损失函数取得最小值或是设置的迭代次数完成为止。以此来计算神经网络中的最佳的参数。

由此，正式介绍BP算法前，我们需要知道前向传播过程，确定网络的设计。为此先设定一个只有一层的神经网络，作为讲解，如图4.

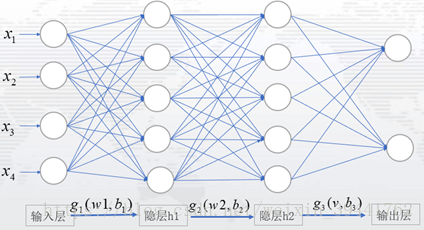
设定：从输入层数据为X，输入层到隐藏层参数为w,b1，隐藏层到输出层参数为v,b2，激活函数用为g1,g2。于是模型设定为：

输入层到隐藏层：

$net_{1} = w^{T}x+b_{1},h=g_{1}(net_{1})$ （3-1）

隐藏层到输出层：

$net_{2} = v^{T}h+b_{2},\hat{y}=g_{2}(net_{2})$ （3-2）

模型：

$\hat{y}=g_{2}(net_{2})=g_{2}(v^{T}g_{1}(net_{1})+b_{2})=g_{2}(v^{T}g_{1}(w^{T}x+b_{1})+b_{2})$ （3-3）

损失函数：

$E(\theta )=\frac{1}{2}\sum_{i=1}^{2} (y_{i}-\hat{y_{i}})^2$ （3-4）

其中：

$x =\begin{pmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{pmatrix},w=\begin{pmatrix} w_{11} &w_{12} &... &w_{15} \\ w_{21}&w_{22} &... &w_{25} \\ w_{31}&w_{32} &... &w_{35} \\ w_{41} &w_{42} &... &w_{45} \end{pmatrix},b_{1}=\begin{pmatrix} b_{11}\\ b_{12}\\ ...\\ b_{14} \end{pmatrix},net_{1}=\begin{pmatrix} net_{11}\\ net_{12}\\ ...\\ net_{14} \end{pmatrix}$

$h =\begin{pmatrix} h_{1}\\ h_{2}\\ ...\\ h_{5} \end{pmatrix},v=\begin{pmatrix} v_{11} &v_{12} \\ v_{21} &v_{22} \\ ... &... \\ v_{51} &v_{52} \end{pmatrix},b_{2}=\begin{pmatrix} b_{21}\\ b_{22} \end{pmatrix},net_{2}=\begin{pmatrix} net_{21}\\ net_{22} \end{pmatrix}$

$\hat{y}=\begin{pmatrix} \hat{y_{1}}\\ \hat{y_{2}} \end{pmatrix},y=\begin{pmatrix} y_{1}\\ y_{2}\end{pmatrix}$

以上述的模型设定为例，下面介绍BP算法步骤，通过BP算法的步骤，了解反向传播，是如何实现模型的参数更新。

实施步骤：

1）初始化网络中的权值和偏置项，分别记为

$w^{(0)},b_{1}^{(0)},v^{(0)},b_{2}^{(0)}$ （3-5）

2）激活前向传播，得到各层输出和损失函数的期望值

$E(\theta )=\frac{1}{2}\sum_{i=1}^{2}(y_{i}-\hat{y_{i}})^{2}$ （3-6）

其中， $\theta$ 表示参数集合， $y$ 表示真实值， $\hat{y}$ 表示预测值， $\frac{1}{2}$ 表示对总的误差值取平均，所以一般情况下，输出单元多少维，误差值求平均就除以多少；本模型设定中，输出值为2维列数据，故用误差值除以2。一般情况下，损失函数的期望值表示为：

$E(\theta )=\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y_{i}})^{2}$ （3-6-1）

这是一组n维数据的输出，若是有m组这样的数据，损失函数的期望值为：

$E(\theta )=\frac{1}{m}\frac{1}{n}\sum_{j=1}^{m}\sum_{i=1}^{n}(y_{ji}-\hat{y}_{ji})^{2}$ （3-6-2）

若真实值与输出值表示为 $y_{n\times m},\hat{y}_{n\times m}$ ，上式可表示为：

$E(\theta )=\frac{1}{mn}(y-\hat{y})^T(y-\hat{y})$ （3-6-3）

一般情况下，输出数据为1维或是2维，输出的数据有多组。

3）根据损失函数，计算输出单元的误差项和隐藏单元的误差项

输出单元的误差项，即计算损失函数关于输出单元的梯度值或偏导数，根据链式法则有：

$\bigtriangledown _{(k)}v=\frac{\partial E}{\partial v}=\frac{\partial net_{2}}{\partial v}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$

$\bigtriangledown _{(k)}b_{2}=\frac{\partial E}{\partial b_{2}}=\frac{\partial net_{2}}{\partial b_{2}}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$ （3-7）

隐藏单元的误差项，即计算损失函数关于隐藏单元的梯度值或偏导数，根据链式法则有：

$\bigtriangledown _{(k)}w=\frac{\partial E}{\partial w}=\frac{\partial net_{1}}{\partial w}\frac{\partial h}{\partial net_{1}}\frac{\partial net_{2}}{\partial h}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$

$\bigtriangledown _{(k)}b_{1}=\frac{\partial E}{\partial b_{1}}=\frac{\partial net_{1}}{\partial b_{1}}\frac{\partial h}{\partial net_{1}}\frac{\partial net_{2}}{\partial h}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$ （3-8）

PS: 对于复合函数中的向量或矩阵求偏导，复合函数内部函数的偏导总是左乘；对于复合函数中的标量求偏导，复合函数内部函数的偏导左乘或者右乘都可以。

4）更新神经网路中的权值和偏置项

输出单元参数更新： $v^{(k)}=v^{(k-1)}-\eta \bigtriangledown _{(k)}v=v^{(k-1)}-\eta \frac{\partial E}{\partial v}, b_{2}^{(k)}=b_{2}^{(k-1)}-\eta \frac{\partial E}{\partial b_{2}}$ （3-9）

隐藏单元参数更新： $w^{(k)}=w^{(k-1)}-\eta \bigtriangledown _{(k)}w=w^{(k-1)}-\eta \frac{\partial E}{\partial w}, b_{1}^{(k)}=b_{1}^{(k-1)}-\eta \frac{\partial E}{\partial b_{1}}$ （3-10）

其中， $\eta$ 表示学习率，k=1,2,...,n表示更新次数或迭代次数，k=1表示第一次更新，以此类推。此处可能和别处博客不太一样，但实质是一样的，此处的'+'或者'-'主要取决于损失函数.

如何定义损失函数或者定义参数更新均可，但参数的更新一定是向参数的负梯度方向。

5）重复步骤2-4，直到损失函数小于事先给定的阈值或迭代次数用完为止，输出此时的参数即为目前最佳参数。

这便是BP算法的一个具体步骤，下面我们详细介绍BP算法步骤中的每一步：

步骤1）初始化参数值(输出单元权值、偏置项和隐藏单元权值、偏置项均为模型的参数)，是为激活前向传播，得到每一层元素的输出值，进而得到损失函数的值。参数初始化，可以自己设定，也可以选择随机生成；一般情况下，自己写代码或者调用tensorflow或keras时，都是随机生成参数。因为初始参数对最终的参数影响不大，只会影响迭代的次数。

步骤2）在步骤1的基础上，激活前向传播，得到 $net_{1},h,net_{2},\hat{y}$ 的值，进而得到的值；其中的计算，根据前面模型设定中的公式计算。计算这些值是为计算步骤3中的误差项。

步骤3）计算各项误差，即计算参数关于损失函数的梯度或偏导数，之所以称之为误差，是因为损失函数本身为真实值与预测值之间的差异。计算参数的偏导数，根据的是微积分中的链式法则。具体推导如下：

输出单元的误差项：输出单元v与损失函数E，不是直接相关，而是通过复合函数的形式关联，以设定的模型为例：

$E(v,b_{2})=\frac{1}{2}\sum_{i=1}^{2}(y_{i}-\hat{y_{i}})^{2}=\frac{1}{2}(y-\hat{y})^T(y-\hat{y})$

$=\frac{1}{2}(y-\hat{y}(net_{2}(v,b_{2})))^T(y-\hat{y}(net_{2}(v,b_{2}))$ （3-11）

其中 $E(v,b_{2})$ 表示损失函数化为与参数v，b2相关的表达式。

根据链式法则，输出单元v与损失函数E的误差项为：

$\bigtriangledown _{(k)}v=\frac{\partial E}{\partial v}=\frac{\partial net_{2}}{\partial v}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$

$\bigtriangledown _{(k)}b_{2}=\frac{\partial E}{\partial b_{2}}=\frac{\partial net_{2}}{\partial b_{2}}\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}$ （3-12）

求出上式中每一个偏导：

$\frac{\partial E}{\partial \hat{y}}=\frac{1}{2\partial \hat{y}}\partial ((y-\hat{y})^T(y-\hat{y}))=\frac{1}{2\partial \hat{y}}\partial (y^Ty-y^T\hat{y}-\hat{y}^Ty+\hat{y}^T\hat{y})$

$=\frac{1}{2}(-y-y+\hat{y}+\hat{y})=\hat{y}-y$ （3-13）

$\frac{\partial \hat{y}}{\partial net_{2}}=\frac{\partial g_{2}(net_{2})}{\partial net_{2}}$ （3-14）

$\frac{\partial net_{2}}{\partial v}=\frac{\partial (v^Th+b_{2})}{\partial v}=h$ （3-15）

$\frac{\partial net_{2}}{\partial b_{2}}=\frac{\partial (v^Th+b_{2})}{\partial b_{2}}=\begin{pmatrix} 1\\ 1\end{pmatrix}^T$ (3-16)

其中， $net_{2}$ 关于激活函数 $g_{2}$ 求偏导，需要根据具体的激活函数而定，每一层的激活函数可以选择不同的函数，一般情况下，为简单化模型设计和求导方便，会设定为同一个函数。此处假设选择激活函数为sigmoid函数，那么有：

$\frac{\partial \hat{y}}{\partial net_{2}}=\frac{\partial g_{2}(net_{2})}{\partial net_{2}}=\begin{pmatrix} \partial sigmoid(net_{21})/\partial net_{21}\\ \partial sigmoid(net_{22})/\partial net_{22}\end{pmatrix}$

$=\begin{pmatrix} \frac{1}{1+exp(-net_{21})}\times(1-\frac{1}{1+exp(-net_{21})}) \\ \frac{1}{1+exp(-net_{22})}\times(1-\frac{1}{1+exp(-net_{22})})\end{pmatrix}=\begin{pmatrix} \hat{y}_{1}(1-\hat{y}_1)\\ \hat{y}_{2}(1-\hat{y}_2)\end{pmatrix}=\hat{y}\bigodot (1-\hat{y})$ (3-17)

PS：因为sigmoid(z)中z是标量，对z求偏导，有：

$\frac{\partial sigmoid(z)}{\partial z}=\frac{\partial (1/(1+exp(-z))}{\partial z}=\frac{exp(-z)}{(1+exp(-z))^2}$

$=\frac{1}{1+exp(-z)}\times \frac{exp(-z)}{1+exp(-z)}=\frac{1}{1+exp(-z)}\times (1-\frac{1}{1+exp(-z)})$

本文定义了z为向量，对于向量就有了式(3-17)的逐元素相乘的式子。

于是，为简化后面的计算，记

$\delta ^{(k)}=\frac{\partial \hat{y}}{\partial net_{2}}\frac{\partial E}{\partial \hat{y}}=\hat{y}\odot (1-\hat{y})\odot (\hat{y}-y)$ (3-18)

其中， $\delta ^{(k)}$ 表示第k次求损失函数关于 $net_{2}$ 的偏导； $\odot$ 表示逐元素相乘，即两个向量或两个矩阵对应的元素相乘，例如：

$\begin{pmatrix} a_{11} &a_{12} \\ a_{21} &a_{22}} \end{pmatrix}\odot \begin{pmatrix} b_{11} &b_{12} \\ b_{21} &b_{22}} \end{pmatrix}=\begin{pmatrix} a_{11}b_{11} &a_{12}b_{12} \\ a_{21}b_{21} &a_{22}b_{22}} \end{pmatrix}$

于是，输出单元的误差项为：

$\bigtriangledown _{(k)}v=\frac{\partial E}{\partial v}=h\cdot \delta ^{(k)T}$ (3-19)

$\bigtriangledown _{(k)}b_{2}=\frac{\partial E}{\partial b_{2}}=\begin{pmatrix} 1\\ 1\end{pmatrix}\odot \delta ^{(k)}=\delta ^{(k)}$ (3-20)

此处说明：若遇式(3-15)的偏导(对权值求偏导)，链式法则处理方式均如式(3-19)；若遇式(3-16)的偏导(对偏置项求偏导)，链式法则处理方式均如式(3-20)。

隐藏单元的误差项：隐藏单元w与损失函数E，通过复合函数的形式关联，以设定的模型整理为：

$E(w,b_{1})=\frac{1}{2}(y-\hat{y})^{T}(y-\hat{y})$

$=\frac{1}{2}(y-\hat{y}(net_{2}(h(net_{1}(w,b_{1}),b_{2}))))^T(y-\hat{y}(net_{2}(h(net_{1}(w,b_{1}),b_{2})))))$ （3-21）

根据链式法则，隐藏单元w与损失函数E的误差项为：

同样的求导法则，得到隐藏单元的误差项为：

$\bigtriangledown _{(k)}w=\frac{\partial E}{\partial w}=x\cdot (h\odot (1-h)\odot (v-\delta ^{(K)}))^T$ （3-23）

$\bigtriangledown _{(k)}b_{1}=\frac{\partial E}{\partial b_{1}}=\begin{pmatrix} 1\\ 1\\ ...\\ 1 \end{pmatrix}\odot (h\odot (1-h)\odot (v\cdot \delta ^{(k)}))=h\odot (1-h)\odot (v\cdot \delta ^{(k)}))$ （3-24）

其中：

$\frac{\partial net_{2}}{\partial h}=\frac{\partial (v^{T}h+b_{2})}{\partial h}=v$ （3-25）

$\frac{\partial h}{\partial net_{1}}=\frac{\partial (sigmoid(net_{1}))}{\partial net_{1}}=h\odot (1-h)$ (3-26)

$\frac{\partial net_{1}}{\partial w}=\frac{(w^Tx+b_{1})}{\partial w}=x$ (3-27)

$\frac{\partial net_{1}}{\partial b_{1}}=\frac{\partial (w^Tx+b)}{\partial b_{1}}=\begin{pmatrix} 1\\ 1\\... \\ 1 \end{pmatrix}^T$ (3-28)

说明：若遇式(3-25)(对隐藏单元求偏导)，链式法则处理如式(3-23)；式(3-15)和(3-26)同，故有相同的处理方式；式(3-16)和(3-27)同，故有相同的处理方式。

补充：若有多个隐藏层时，逐步计算隐藏层的权值和偏置项误差，推导的规则同上。例如：一个隐藏层为2，隐藏单元为5的神经网络：

输出层到隐藏层2的误差项同式(3-19)

隐藏层2到隐藏层1的误差项为：

$\bigtriangledown _{(k)}w2=\frac{\partial E}{\partial w2}=h_{1}\cdot (h_{2}\odot (1-h_{2})\odot (v\cdot \delta ^{(k)}))^T$ (3-29)

记：

$\delta _{1}^{(k)}=h_{2}\odot (1-h_{2})\odot (v\cdot \delta ^{(k)})^T$ (3-30)

隐藏层1到输入层的误差项为：

$\bigtriangledown _{(k)}w1=\frac{\partial E}{\partial w1}=x\cdot (h_{1}\odot (1-h_{1})\odot (w2\cdot \delta _{1}^{(k)}))^T$ (3-31)

从上述中，容易看出，无论多少层隐藏层，其误差项都是同样的结构。

步骤4）更新神经网路中的权值和偏置项。学习率自己设定，学习率太大，容易跳过最佳的参数；学习率太小，容易陷入局部极小值。

步骤5）设定阈值e或者设定迭代次数，当损失函数值小于阈值e时，或当迭代次数用完时，输出最终参数。

4、实例运用

为能更好理解BP算法和知道如何运用BP算法，下面以一个实际的例子来说明运用BP算法的具体操作。

有一组数据 $X=\begin{bmatrix} 0.05\\ 0.10\end{bmatrix},Y=\begin{bmatrix} 0\\ 1\end{bmatrix}$ ，目的是训练这两组数据，找到输入X计算得到Y的预测值尽可能接近于真实值的参数。设定模型：设计一个隐藏层为1，隐藏单元数为2，激活函数为sigmod函数的模型，运用反向传播算法，得到参数。网络如图5：

于是有：

$x=\begin{bmatrix}x_{1}\\ x_{2}\end{bmatrix}, w=\begin{bmatrix}w_{11} &w_{12} \\ w_{21}&w_{22} \end{bmatrix}, b_{1}=\begin{bmatrix}b_{11}\\ b_{12}\end{bmatrix}, h=\begin{bmatrix}h_{1}\\ h_{2}\end{bmatrix}$

$v=\begin{bmatrix}v_{11} &v_{12} \\ v_{21}&v_{22} \end{bmatrix}, b_{2}=\begin{bmatrix}b_{21}\\ b_{22}\end{bmatrix}, \hat{y}=\begin{bmatrix}\hat{y}_{1}\\ \hat{y}_{2}\end{bmatrix}$

$net_{1}=w^Tx+b_{1},h=sigmoid(net_{1})$

$net_{2}=v^Tx+b_{2},h=sigmoid(net_{2})$ (4-1)

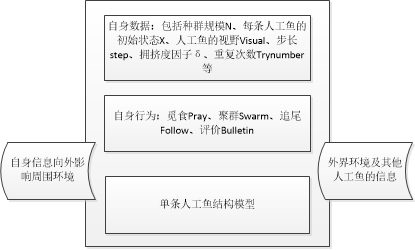
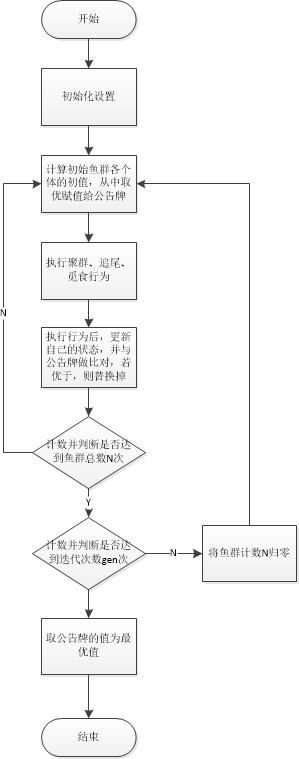
式(4-1)中，x表示net1后的h。

根据BP算法步骤：

1）初始化网络中的所有参数并给出学习率 $\eta$ ：

$w=\begin{bmatrix}0.15 &0.20 \\ 0.25 &0.30 \end{bmatrix}, b_{1}=\begin{bmatrix}0.1\\ 0.1\end{bmatrix}, v=\begin{bmatrix}0.40 &0.45 \\ 0.50 &0.55 \end{bmatrix}, b_{2}=\begin{bmatrix}0.2\\ 0.2\end{bmatrix},\eta =0.5$

2）激活前向传播，将参数带入式(4-1)，并计算损失函数：

输入层-->隐藏层：

$net_{1}=w^Tx+b_{1}=\bigl(\begin{smallmatrix} 0.15*0.05+0.25*0.1+0.1\\ 0.20*0.05+0.30*0.1+0.1 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 0.1325\\ 0.1400 \end{smallmatrix}\bigr)$ (4-2)

$h=sigmoid(net_{1})=sigmoid\bigl(\begin{smallmatrix} 0.1325\\ 0.1400\end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 0.5331\\ 0.5349 \end{smallmatrix}\bigr)$ (4-3)

隐藏层-->输出层：

$net_{2}=v^Tx+b_{2}=\bigl(\begin{smallmatrix} 0.40*0.5331+0.5*0.5349+0.2\\ 0.45*0.5331+0.55*0.5349+0.2 \end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 0.6807\\ 0.7341 \end{smallmatrix}\bigr)$ (4-4)

（上式中x表示4-3中的h）

$\hat{Y}=sigmoid(net_{2})=sigmoid\bigl(\begin{smallmatrix} 0.6807\\ 0.7341\end{smallmatrix}\bigr)=\bigl(\begin{smallmatrix} 0.6639\\ 0.6575 \end{smallmatrix}\bigr)$ (4-5)

损失函数：

$E(\theta )=\frac{1}{2}(Y-\hat{Y})^T(Y-\hat{Y})=\frac{1}{2}\bigl(\begin{smallmatrix} 0-0.6639\\ 1-0.6757 \end{smallmatrix}\bigr)=0.2796$ (4-6)

3）计算输出单元的误差项和隐藏单元的误差项

输出单元的误差项：根据公式(3-19)，将 $Y,\hat{Y},net_{2},h$ 带入其中，得到需更新的梯度误差：

$\delta ^{(1)}=\hat{Y}\odot (1-\hat{Y})\odot (\hat{Y}-Y)=\begin{pmatrix} \hat{y}_{1}\\ \hat{y}_{2}\end{pmatrix}\odot \begin{pmatrix} 1-\hat{y}_{1}\\ 1-\hat{y}_{2}\end{pmatrix}\odot \begin{pmatrix} \hat{y}_{1}-y_{1}\\ \hat{y}_{2}-y_{2} \end{pmatrix}$

$=\begin{pmatrix}0.6639\\0.6757 \end{pmatrix}\odot \begin{pmatrix}1-0.6639\\ 1-0.6757\end{pmatrix}\odot \begin{pmatrix}0.6639-0\\ 0.6757-1\end{pmatrix}=\begin{pmatrix} 0.14814\\ -0.07106 \end{pmatrix}$

$\bigtriangledown _{1}v =h\cdot \delta ^{(1)}^T=\begin{pmatrix}0.5331\\ 0.5349\end{pmatrix}\cdot \begin{pmatrix}0.14814\\ -0.07106\end{pmatrix}^{T}=\begin{pmatrix}0.07897 &-0.03788 \\ 0.07924 &-0.03801 \end{pmatrix}$

如果对v中每一个元素求偏导，有：

$\bigtriangledown _{1}v_{11}=(\hat{y}_{1}-y_{1})(\hat{y}_{1}(1-\hat{y}_{1}))h_{1}=0.07897$

$\bigtriangledown _{1}v_{12}=(\hat{y}_{2}-y_{2})(\hat{y}_{2}(1-\hat{y}_{2}))h_{1}=-0.03788$

$\bigtriangledown _{1}v_{21}=(\hat{y}_{1}-y_{1})(\hat{y}_{1}(1-\hat{y}_{1}))h_{2}=0.07924$

$\bigtriangledown _{1}v_{22}=(\hat{y}_{2}-y_{2})(\hat{y}_{2}(1-\hat{y}_{2}))h_{2}=-0.03801$

$\bigtriangledown _{1}v=\begin{pmatrix} 0.07897 &-0.03788 \\ 0.07924&-0.03801 \end{pmatrix}$

用公式(3-19)和对v中每一个元素求偏导，得到的结果一致。

隐藏单元的误差项：根据公式(3-23)，将 $\delta ^{(1)},net_{1},h,v,x$ 带入其中，得到需更新的梯度误差

$\bigtriangledown _{1}w=x\cdot (h\odot (1-h)\odot (v\cdot \delta ^{(1)}))^T$

$=\begin{pmatrix}x_{1}\\ x_{2}\end{pmatrix}\cdot\left ( \begin{pmatrix} h_{1}\\h_{2} \end{pmatrix}\odot \begin{pmatrix}1-h_{1}\\1-h_{2} \end{pmatrix} \odot \left ( \begin{pmatrix}v_{11} &v_{12} \\ v_{21} &v_{22} \end{pmatrix}\cdot \delta ^{(1)} \right )\right )^T$

$=\begin{pmatrix}0.05\\ 0.10\end{pmatrix}\cdot\left ( \begin{pmatrix} 0.5331\\0.5349 \end{pmatrix}\odot \begin{pmatrix}1-0.5331\\1-0.5349 \end{pmatrix} \odot \left ( \begin{pmatrix}0.40 &0.45 \\ 0.50 &0.55\end{pmatrix}\cdot\begin{pmatrix}0.14814\\-0.007106 \end{pmatrix} \right )\right )^T$

$=\begin{pmatrix}0.05\\0.10 \end{pmatrix}\cdot \begin{pmatrix}0.02728\\0.03499 \end{pmatrix}^T=\begin{pmatrix} 1.364\times 10^{-3} & 1.750\times 10^{-3}\\ 2.728\times 10^{-3}&3.500\times 10^{-3} \end{pmatrix}$

若对w中每一个元素求偏导，有：

$\bigtriangledown _{1}w_{11}=x_{1}(h_{1}(1-h_{1})v_{11}\delta _{1}^{(1)}+h_{1}(1-h_{1})v_{12}\delta _{2}^{(1)})=1.364\times 10^{-3}$

$\bigtriangledown _{1}w_{12}=x_{1}(h_{2}(1-h_{2})v_{21}\delta _{1}^{(1)}+h_{2}(1-h_{2})v_{22}\delta _{2}^{(1)})=1.750\times 10^{-3}$

$\bigtriangledown _{1}w_{21}=x_{2}(h_{1}(1-h_{1})v_{11}\delta _{1}^{(1)}+h_{1}(1-h_{1})v_{12}\delta _{2}^{(1)})=2.728\times 10^{-3}$

$\bigtriangledown _{1}w_{22}=x_{2}(h_{2}(1-h_{2})v_{21}\delta _{1}^{(1)}+h_{2}(1-h_{2})v_{22}\delta _{2}^{(1)})=3.500\times 10^{-3}$

$\bigtriangledown _{1}w=\begin{pmatrix} \bigtriangledown _{1}w_{11}& \bigtriangledown _{1}w_{12} \\ \bigtriangledown _{1}w_{21}& \bigtriangledown _{1}w_{22} \end{pmatrix}=\begin{pmatrix} 1.364\times 10^{-3} &1.750\times 10^{-3} \\ 2.728\times 10^{-3}&3.500\times 10^{-3} \end{pmatrix}$

用公式(3-23)和对v中每一个元素求偏导，得到的结果一致。

注意：一般情况下，不会对偏置项更新

4）更新神经网络中的权值

$v^{(1)}=v^{(0)}-\eta \ast \bigtriangledown _{1}v=\begin{pmatrix}0.40 &0.45 \\ 0.50 &0.55 \end{pmatrix}-0.5\ast \begin{pmatrix}0.07897 &-0.03788 \\ 0.07924 &-0.03801 \end{pmatrix}$

$=\begin{pmatrix}0.36051 &0.46894 \\ 0.46038 &0.56901 \end{pmatrix}$

$w^{(1)}=w^{(0)}-\eta \ast \bigtriangledown _{1}w=\begin{pmatrix}0.15 &0.20\\ 0.25 &0.30 \end{pmatrix}-0.5\ast \begin{pmatrix}1.364\times 10^{-3} &1.750\times 10^{-3} \\ 2.728\times 10^{-3} &3.500\times 10^{-3} \end{pmatrix}$

$=\begin{pmatrix}0.14983 &0.19978 \\ 0.24966 &0.29956 \end{pmatrix}$

于是，得到第一次更新的参数值w,v。

5）重复步骤2-4，直到损失值达到了预先设定的阈值或迭代次数用完，得到最终的权值。

1.2 人工鱼群算法

1.2.1 人工鱼的结构模型

人工鱼是真实鱼抽象化、虚拟化的一个实体，其中封装了自身数据和一系列行为，可以接受环境的刺激信息，做出相应的活动。其所在的环境由问题的解空间和其他人工鱼的状态，它在下一时刻的行为取决于自身的状态和环境的状态，并且它还通过自身的活动来影响环境，进而影响其他人工鱼的活动。

1.2.2 人工鱼群算法的寻优原理

人工鱼群算法在寻优的过程中，可能会集结在几个局部最优解的周围，使人工鱼跳出局部最优解，实现全局寻优的因素主要有：

觅食行为中重复次数较少时，为人工鱼提供了随机移动的机会，从而可能跳出局部最优解；随机步长使得人工鱼在前往局部最优解的途中，有可能转向全局最优解；拥挤度因子 δδ 限制了聚群的规模，使得人工鱼能够更广泛的寻优；聚群行为能够促使少出陷于局部最优解的人工鱼趋向全局最优解的人工鱼方向聚集，从而逃出局部最优解；追尾行为加快了人工鱼向更优状态游动。

1.2.3 人工鱼群算法实现的步骤

初始化设置，包括种群规模N、每条人工鱼的初始位置、人工鱼的视野Visual、步长step、拥挤度因子δ、重复次数Trynumber；计算初始鱼群各个体的适应值，取最优人工鱼状态及其值赋予给公告牌；对每个个体进行评价，对其要执行的行为进行选择，包括觅食Pray、聚群Swarm、追尾Follow和评价行为bulletin；执行人工鱼的行为，更新自己，生成新鱼群；评价所有个体。若某个体优于公告牌，则将公告牌更新为该个体；当公告牌上最优解达到满意误差界内或者达到迭代次数上限时算法结束，否则转步骤3。

1.2.4 人工鱼群算法实现流程图

1.2.5 各种参数对收敛性的影响

人工鱼群算法中，觅食行为奠定了算法收敛的基础；聚群行为增强了算法收敛的稳定性；追尾行为增强了算法收敛的快速性和全局性；其评价行为也对算法收敛的速度和稳定性提供了保障。

人工鱼群算法有5个基本参数：群规模N、人工鱼的视野Visual、步长Step、拥挤度因子δ、重复次数Trynumber。 1. 视野Visual：由于视野对算法中个行为都有较大影响，因此，它的变化对收敛性能影响也比较复杂。当视野范围较小时，人工鱼的觅食行为和随机行为比较突出；视野范围较大时，人工鱼的追尾行为和聚群行为将变得比较突出，相应的算法的复杂度也会有所上升。总的来说：视野越大，越容易使人工鱼发现全局最优解并收敛。 2. 步长Step：对于固定步长，随着步长的增加，收敛的速度得到了一定的加速，但在超过一定的范围后，有使得收敛速度减缓，步长过大时会出现震荡现象而大大影响收敛速度。采用随机步长的方式在一定程度上防止了震荡现象的发生，并使得该参数的敏感度大大降低了，但最快的收敛速度还是最优固定步长的收敛速度，所以，对于特定的优化问题，我们可以考虑采用合适的固定步长或者变尺度方法来提高收敛速度。 3. 群规模N：人工鱼的数目越多，跳出局部最优解的能力越强，同时，收敛的速度也越快。当然，付出的代价就是算法每次迭代的计算量也越大，因此，在使用过程中，满足稳定收敛的前提下，应当尽可能的减少个图数目。 4. 尝试次数Trynumber：尝试次数越多，人工鱼的觅食行为能力越强，收敛的效率也越高。在局部极值突出的情况下，应该适当的减少以增加人工鱼随机游动的概率，克服局部最优解。 5. 拥挤度因子δ：在求极大值问题中，δ=1/(αnmax),α∈(0,1]δ=1/(αnmax),α∈(0,1]；在求极小值问题中，δ=αnmax,α∈(0,1]δ=αnmax,α∈(0,1]。其中α为极值接近水平， nmax为期望在该邻域内聚集的最大人工鱼数目。拥挤度因子与nf相结合，通过人工鱼是否执行追尾和聚群行为对优化结果产生影响。以极大值为例（极小值的情况正好与极大值相反），δ越大，表明允许的拥挤程度越小，人工鱼摆脱局部最优解的能力越强；但是收敛速度会有所减缓，这主要因为人工鱼在逼近最优解的同时，会因避免过分拥挤而随机走开或者受其他人工鱼的排斥作用，不能精确逼近极值点。可见，虽然δ的引入避免了人工鱼过度拥挤而陷入局部最优解，但是另一方面，该参数会使得位于极值点附件的人工鱼之间存在相互排斥的影响，而难以想极值点精确逼近。所以，对于某些局部极值不是很严重的具体问题，可以忽略拥挤的因素，从而在简化算法的同时也加快算法的收敛速度和提高结果的精确程度。

2 部分代码 %%%%%%%%%%%%人工鱼算法优化BP神经网络（所有数据未随机抽取）%%%%%%%%%%%%%%%%%%%%%%%%% tic; %计时开始 clc; %清屏 clear all; %清除所有变量 close all; load gqpin.txt;data1=gqpin; load gqpout.txt;data2=gqpout; data1=data1'; data2=data2'; for i=1:5 data1(i,:)=(data1(i,:)-min(data1(i,:)))/(max(data1(i,:))-min(data1(i,:))); end for i=1:1 data2(i,:)=(data2(i,:)-min(data2(i,:)))/(max(data2(i,:))-min(data2(i,:))); end data11=data1'; data22=data2'; x1=data11(:,1); y1=data22; x2=data11(:,2); y2=data22; x3=data11(:,3); y3=data22; x4=data11(:,4); y4=data22; x5=data11(:,5); y5=data22; X_sample=[x1,x2,x3,x4,x5]; %X(261,5) Y_sample=[y1,y2,y3,y4,y5]; %Yo(261,5) input=size(X_sample,1); %输入层神经元个数 middle=100; %显示中间层神经元个数 output=size(X_sample,1); %显示输出层神经元个数261 %%%% v=rands(input,middle); %初始化连接权矩阵v(i,j) :输入层与中间层的连接权 w=rands(middle,output); %初始化连接权矩阵w(j,t) :中间层与输出层的连接权 th1=rands(middle,1); %初始化中间层阈值矩阵th1 :中间层的阈值 th2=rands(output,1); %初始化输出层阈值矩阵th2 :输出层的阈值 out_middle=zeros(middle,1); %中间层的实际输出 out_output=zeros(output,1); %输出层的实际输出 delta_output=zeros(output,1); %输出层的差值 delta_middle=zeros(middle,1); %中间层的差值 sample_bumbers=5; %样本数 max_times=3; %最大训练次数 times=0; %训练次数 eta=0.1; %学习系数eta gamma=0.1; %学习系数gamma alpha=0.3; %动量系数 sample_pointer=0; %样本数指针 error_max=0.01; %最大误差 error_global=1; %全局误差 %%%%%%人工鱼算法初始化%%%%%%%%%%% fishnum=50; %生成50条人工鱼 MAXGEN=10; %最大迭代次数 try_number=50; %最大试探次数 visual=1; %感知距离 delta=0.618; %拥挤度因子 step=0.01; %移动步长 for times=1:max_times %begin for External Loop end %计算输出层输出： Y=w'*out_middle-th2; %Y(3,1)=w'(3,8)*out_middle(8,1)*-th2(3,1)，计算输出层的输入 output_error(sample_pointer)=0 for k=1:output %k=1:3 end %计算下一次的中间层和输出层之间的连接权w(i,j)，阈值th2(j) pre_w=0;pre_th2=0; for k=1:output; for j=1:middle w(j,k)=w(j,k)+eta*delta_output(k)*out_middle(j)+alpha*pre_w; %out_middle(j)=y(j) pre_w=eta*delta_output(k)*out_middle(j); end th2(k)=th2(k)+eta*delta_output(k)+alpha*pre_th2; pre_th2=eta*delta_output(k); end disp('^^^^^^^^^^^^^显示结果：^^^^^^^^^^^^^^'); fprintf('总训练次数为：%d.\n',times); fprintf('运行时间为：\n'); toc; %计时结束，并输出程序的运行时间 figure(1) plot(out_output,'r--'); hold on grid on plot(Y0,'b-'); legend('模型输出','实际输出'); figure(2) plot(Y0-out_output,'-'); grid on xlabel('输入样本'),ylabel('样本输出误差'),title('E误差'); 3 仿真结果

4 参考文献

[1]陈群, 左锋, 卢文科. 基于人工鱼群BP神经网络算法的压力传感器温度补偿研究[J]. 微型机与应用, 2016, 35(009):27-29.

5 代码下载

【本文地址】

【预测模型】基于人工鱼群算法优化BP神经网络实现数据预测matlab源码

【预测模型】基于人工鱼群算法优化BP神经网络实现数据预测matlab源码

今日新闻

推荐新闻