深度学习(神经网络) |
您所在的位置:网站首页 › narx神经网络和bp神经网络原理差异 › 深度学习(神经网络) |
深度学习(神经网络)
|
深度学习(神经网络) —— BP神经网络原理推导及python实现
摘要(一)BP神经网络简介1、神经网络权值调整的一般形式为:2、BP神经网络中关于学习信号的求取方法:
(二)BP神经网络原理推导1、变量说明2、BP算法推导
(三)BP神经网络python实现1、模型所需传参介绍2、模型具有的主要方法和属性3、python代码4、代码运行结果
摘要
本文首先介绍了BP神经网络求取学习信号的方法,其次对BP神经网络在原理上进行了推导,最后在python上进行编程实现,并将其封装,方便读者直接调用。 (一)BP神经网络简介BP神经网络是整个神经网络体系中的精华,与一般神经网络相比,它调整权值方式为从最后一层开始逐层调整,通过多次迭代,使得代价函数降低至可接受范围。因此,这就是BP神经网络的来源(Back Propagation,误差反向传播)。 1、神经网络权值调整的一般形式为:
假设一个神经网络共n层 (1)以三层感知器构成的神经网络为例(实际为两层神经网络)。 (1)构建计算输出层输出的函数 如果读者想自己动手在python上实现BP神经网络的话,可以根据文章给出的关于学习信号的求取方法进行编程,本文给出了自己的实现代码,且将其封装成一个类,基本上的属性和方法都具有,通用性较强,读者既可调用其来训练自己的模型,也可以参考其架构自行编写代码。 1、模型所需传参介绍 layer 为神经网络各层神经元的个数,包括输出层神经元个数,传参形式以列表传入; activate:为各层的激活函数,传参形式为字符串或列表, 若传入一个字符串,则各层激活函数相同, 若传入一个列表,则列表元素代表各层激活函数 可传参数有: (1)sigmoid:S型函数 (2)tanh:双曲正弦函数 (3)relu:max(0,x)函数 (4)purline:线性函数 (5)softsign:平滑函数 lr:学习率,默认为0.01 epoch:最大迭代次数 默认为1e4 2、模型具有的主要方法和属性 fit(X,Y):模型拟合方法 predict(X):输出预测方法 predict_label(X):分类标签输出预测方法 activate:激活函数列表 W:权值列表 3、python代码 import numpy as np import time class Cyrus_BP(object): """ layer 为神经网络各层神经元的个数,包括输出层神经元个数,传参形式以列表传入; activate:为各层的激活函数,传参形式为字符串或列表, 若传入一个字符串,则各层激活函数相同, 若传入一个列表,则列表元素代表各层激活函数 可传参数有:(1)sigmoid:S型函数 (2)tanh:双曲正弦函数 (3)relu:max(0,x)函数 (4)purline:线性函数 (5)softsign:平滑函数 lr:学习率,默认为0.01 epoch:最大迭代次数 默认为1e4 该模型具有的主要方法和属性如下: fit(X,Y):模型拟合方法 predict(X):输出预测方法 predict_label(X):分类标签输出预测方法 activate:激活函数列表 W:权值列表 """ def __init__(self,layer,**kargs): self.layer = np.array(layer).reshape(1,-1) if 'activate' in kargs.keys(): if str(type(kargs["activate"])) == "": self.activate = [kargs["activate"]]*int(len(layer)) else: self.activate = kargs["activate"] else: self.activate = ["sigmoid"]*int(len(layer)) self.diff_activate = [] if 'lr' in kargs.keys(): self.lr = kargs["lr"] else: self.lr = 0.01 if 'epoch' in kargs.keys(): self.epoch = kargs["epoch"] else: self.epoch = int(1e4) self.X = None self.Y = None self.W = None self.output = [] self.delta = [] self.sum_input = [] # 1、选择激活函数 def activation_func(self): temp_func = [] for i in range(len(self.activate)): if self.activate[i] == "sigmoid": temp_func.append(lambda x:1/(1+np.exp(-x))) self.diff_activate.append(lambda x:(1/(1+np.exp(-x)))*(1-(1/(1+np.exp(-x))))) if self.activate[i] == "tanh": temp_func.append(lambda x:(np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))) self.diff_activate.append(lambda x:((-np.exp(x) + np.exp(-x))*(np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))**2 + 1)) if self.activate[i] == "softsign": temp_func.append(lambda x:x/(1+np.abs(x))) self.diff_activate.append(lambda x:1/((1+x/np.abs(x)*x)**2)) if self.activate[i] == "relu": temp_func.append(lambda x:(x+np.abs(x))/(2*np.abs(x))*x) self.diff_activate.append(lambda x:(x+np.abs(x))/(2*np.abs(x))) if self.activate[i] == "purline": temp_func.append(lambda x:x) self.diff_activate.append(lambda x:1+x-x) self.activate = temp_func # 2、权值初始化函数 def init_w(self): self.W = [] for i in range(self.layer.shape[1]): if i == 0: w = np.random.random([self.X.shape[1]+1,self.layer[0,i]])*2-1 else: w = np.random.random([self.layer[0,i-1]+1,self.layer[0,i]])*2-1 self.W.append(w) # 3、权值调整函数 def update_w(self): # 1 计算各层输出值 self.output = [] self.sum_input = [] for i in range(self.layer.shape[1]): if i == 0: temp = np.dot(np.hstack((np.ones((self.X.shape[0],1)),self.X)),self.W[i]) self.sum_input.append(temp) self.output.append(self.activate[i](temp)) else: temp = np.dot(np.hstack((np.ones((self.output[i-1].shape[0],1)),self.output[i-1])),self.W[i]) self.sum_input.append(temp) self.output.append(self.activate[i](temp)) # 2 求每层的学习信号 self.delta = [0 for i in range(len(self.output))] for i in range(len(self.output)): if i == 0: self.delta [-i-1] = ((self.Y-self.output[-i-1])*self.diff_activate[-i-1](self.sum_input[-i-1])) else: self.delta [-i-1] = ((self.delta[-i].dot(self.W[-i][1:,:].T))*self.diff_activate[-i-1](self.sum_input[-i-1])) # 3 更新权值 for i in range(len(self.W)): if i == 0 : self.W[i] += self.lr * np.hstack((np.ones((self.X.shape[0],1)),self.X)).T.dot(self.delta[i]) else: self.W[i] += self.lr * np.hstack((np.ones((self.output[i-1].shape[0],1)),self.output[i-1])).T.dot(self.delta[i]) def fit(self,X,Y): self.X = np.array(X) self.Y = np.array(Y) # 1 权值初始化 self.init_w() # 2 选择激活函数 self.activation_func() # 3 更新权值 start_time = time.time() for i in range(int(self.epoch)): self.update_w() end_time = time.time() if end_time - start_time >= 5: print("Epoch%d:"%(i+1),np.mean(np.square(self.Y-self.output[-1]))) print("\n") start_time = time.time() def predict(self,x): x = np.array(x) result = [] for i in range(self.layer.shape[1]): if i == 0: result.append(self.activate[i](np.dot(np.hstack((np.ones((x.shape[0],1)),x)),self.W[i]))) else: result.append(self.activate[i](np.dot(np.hstack((np.ones((result[i-1].shape[0],1)),result[i-1])),self.W[i]))) return result[-1] def predict_label(self,x): x = np.array(x) result = [] for i in range(self.layer.shape[1]): if i == 0: result.append(self.activate[i](np.dot(np.hstack((np.ones((x.shape[0],1)),x)),self.W[i]))) else: result.append(self.activate[i](np.dot(np.hstack((np.ones((result[i-1].shape[0],1)),result[i-1])),self.W[i]))) result = result[-1] return np.array([result[i].argmax() for i in range(result.shape[0])]).reshape(-1,1) if __name__ == "__main__": bp = Cyrus_BP([50,10,3],lr=0.01,epoch = 2e5,activate = ["softsign","softsign","softsign"]) from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score data = load_iris() X = data["data"] Y = data["target"] import pandas as pd # 用神经网络进行分类时,需把输出先进行独热编码 Y1 = pd.get_dummies(Y1) # 进行独热编码或将期望输出转换为哑变量 bp.fit(X,Y1) Y_pre = bp.predict_label(X) print("准确率为:",accuracy_score(Y,Y_pre)) 4、代码运行结果 Epoch9314: 0.02853577904298399 Epoch19691: 0.02145897246261971 Epoch31495: 0.01784770845276102 Epoch42539: 0.01415043927077651 Epoch53434: 0.015407038745481208 Epoch64893: 0.016390764988851683 Epoch76186: 0.015016316993973523 Epoch86931: 0.013693150044879728 Epoch97390: 0.013706384360315056 Epoch108511: 0.012193768543380657 Epoch118993: 0.010314480349340294 Epoch128337: 0.009862103298377766 Epoch138193: 0.01057658278951552 Epoch147889: 0.009652582210903272 Epoch157632: 0.009137051214565095 Epoch165815: 0.009407398018203143 Epoch175037: 0.009429640020604707 Epoch185229: 0.00991562156191445 Epoch194220: 0.009801710064963167 准确率为: 0.9933333333333333可见模型训练结果还是不错的 by CyrusMay 2020 05 11 晚风吻尽 荷花叶 任我醉倒在池边 等你清楚看见我的美 月光晒干眼泪 ——五月天(拥抱)—— |
【本文地址】
今日新闻 |
推荐新闻 |
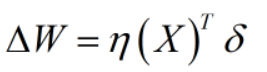 (1)其中 η为学习率,可以理解为每次权值调整的步长 (2)其中δ为学习信号,可以理解为每次权值调整的方向,实际上为一个梯度向量。 由上式也可以发现不同神经网络的差异主要体现在学习信号上的差异。
(1)其中 η为学习率,可以理解为每次权值调整的步长 (2)其中δ为学习信号,可以理解为每次权值调整的方向,实际上为一个梯度向量。 由上式也可以发现不同神经网络的差异主要体现在学习信号上的差异。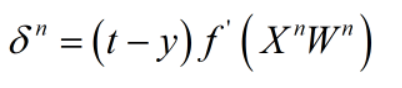 上式为求取最后一层,即输出层的学习信号,其中t为期望输出,y为模型输出,f(x)为激活函数(对激活函数不了解的可自行先百度或查看我的其他文章)。
上式为求取最后一层,即输出层的学习信号,其中t为期望输出,y为模型输出,f(x)为激活函数(对激活函数不了解的可自行先百度或查看我的其他文章)。 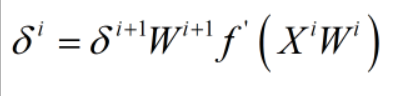 上式为求取除最后一层以外其他层的学习信号,i+1表示第i层后面的一层,可以发现求取第i层学习信号时,需要先求取出第i+1层的学习信号,这也是误差反向传播的来源。 具体BP神经网络的学习信号推导过程见以下的原理推导,推导过程有点小复杂,即使不看,根据以上的结论也可以编写自己的BP神经网络程序了。
上式为求取除最后一层以外其他层的学习信号,i+1表示第i层后面的一层,可以发现求取第i层学习信号时,需要先求取出第i+1层的学习信号,这也是误差反向传播的来源。 具体BP神经网络的学习信号推导过程见以下的原理推导,推导过程有点小复杂,即使不看,根据以上的结论也可以编写自己的BP神经网络程序了。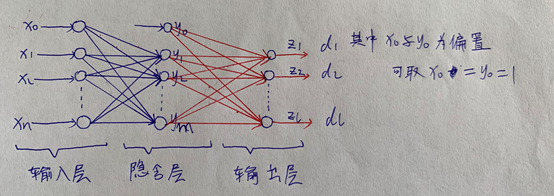 (2)定义各层的输入和输出: 输入向量 隐含层输出向量 输出层输出向量 期望输出向量
(2)定义各层的输入和输出: 输入向量 隐含层输出向量 输出层输出向量 期望输出向量 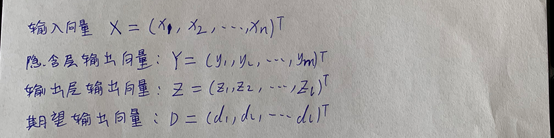 (3)定义权值矩阵: 输入层到隐含层的权值矩阵 隐含层到输出层的权值矩阵
(3)定义权值矩阵: 输入层到隐含层的权值矩阵 隐含层到输出层的权值矩阵  (4)设定激活函数
(4)设定激活函数 
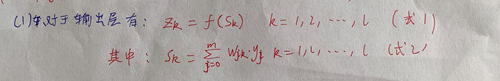 (2)构建计算隐含层输出的函数
(2)构建计算隐含层输出的函数 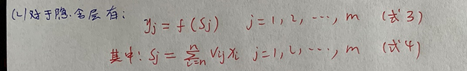 (3)定义代价函数
(3)定义代价函数  (4)式9中x与d分别为输入与对应的期望输出,皆为已知,所以代价函数则为两个权值矩阵的函数,为了使代价函数减小,权值的调整应往负梯度方向调整,如下:(η为学习率,可以理解为往负梯度方向改变的步长)
(4)式9中x与d分别为输入与对应的期望输出,皆为已知,所以代价函数则为两个权值矩阵的函数,为了使代价函数减小,权值的调整应往负梯度方向调整,如下:(η为学习率,可以理解为往负梯度方向改变的步长)  (5)将式10和式11按链式求导法则进行展开:
(5)将式10和式11按链式求导法则进行展开:  (6)对输出层和隐含层各定义一个误差信号(本质上为负梯度):
(6)对输出层和隐含层各定义一个误差信号(本质上为负梯度):  (7)将式14和式15代入式12和式13,得:
(7)将式14和式15代入式12和式13,得:  (8)求解输出层和隐含层的学习信号(需结合式1和式3):
(8)求解输出层和隐含层的学习信号(需结合式1和式3): 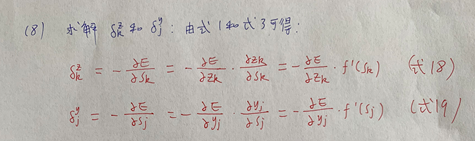 (9)计算式18和19中的偏导:
(9)计算式18和19中的偏导:  (10)将式20和式21带回式18和19:
(10)将式20和式21带回式18和19: 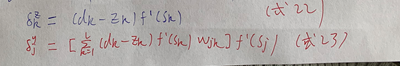 (11)将式22)和式23带回式16和17,得:
(11)将式22)和式23带回式16和17,得: 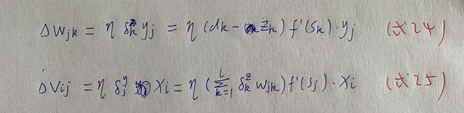 (12)将三层感知器推广到任意层数神经网络: 假设神经网络共n层。
(12)将三层感知器推广到任意层数神经网络: 假设神经网络共n层。 