本节将就线性代数中的部分内容讲解MATLAB中的简单的基础操作，且依旧不涉及编程内容

1.计算行列式的值：

MATLAB中用的是det指令,det(A)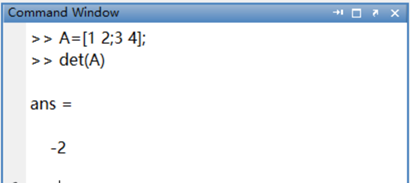

如果是线性方程组求解的话，这里介绍第一种方法：

我们以书上的例题为例：

5x + 2y - 9z = -18

-9x - 2y + 2z = -7

6x + 7y + 3z = 29

首先，简单分析一波，这是个非齐次的线性方程组，我们又知道方程组想要非齐次线性方程组有解的条件是系数矩阵为满秩，满秩的性质之一为该矩阵行列式不为0. 所以我们接下来只要求det(A)即可。

接下来用系数矩阵左除即可：

2.秩的求法

MATLAB中函数rank(A)用于求解秩，这里的例子依旧是上述的系数矩阵

于是，我们又有了一个新的方法去求解线性方程组的解了

5x + 2y - 9z = -18

-9x - 2y + 2z = -7

6x + 7y + 3z = 29

TIPS：

回顾一下线性代数的知识，我们知道，对线性方程组Ax=b有解的条件是R(A)=R(A,b)

对非齐次线性方程组来说

R(A)=R(A,b)

Continue

对Ax=b，无论其有没有解，或者有多解，MATLAB都可以给出唯一解，且：

①若方程组有无穷多的解，MATLAB给出的是最小范数解。

②若方程组没有解，MATLAB会给出最小二乘解。

PS：大家应该都是工科生，看的也是同济大学的线性代数，这个小点可以略去，想了解的可以看看矩阵论，另外强推bilibili上面的3Blue1Brown的视频，直观理解线性代数的神器。

3.逆矩阵

MATLAB中的inv()函数用于计算逆矩阵。

但是，逆矩阵不是一直存在的，逆矩阵存在的充要条件为：

矩阵行列式不为0

矩阵为满秩（废话）

矩阵合同标准型为单位矩阵

所以，在MATLAB计算逆矩阵时，先计算其行列式 或秩，会比较稳妥。

我们又有了一种新的方法去求线性方程组的解了：

若Ax=b,那么

这里不做演示。

刚刚提到的最小范数解在这有所应用

当 det(A) = 0 时，方程组存在无限解，此时我们可以求伪逆矩阵：找到最小范数实数解，即，解向量x具有最小范数且元素都为实数

对下示例子：我们很明显的知道它有无限个解

对于这种情况我们使用pinv（A）求其伪逆

Tips：1.对于非奇异方阵，我们可以用inv(A).

2.对于奇异方阵或者是非方阵，我们采用pinv(A

3实际应用的时候我们不需要写成inv(A*B,直接写成A\B即可，对于B*inv(A),写成B/A即可。

4.简化矩阵：

处有个有趣的小例子——魔方矩阵。魔方矩阵是一个n阶方阵。矩阵的元素从1到 ，并且满足行元素的和等于列元素的和。MATLAB中提供了magic(n)指令帮助我们去计算：

此时我们来检查一下每列的和：

检查一下列和：

Perfect.

接着我们在对其进行简化：

5.矩阵分解（仅指LU分解）

回顾一下，LU分解是将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积。在matlab中写成[L U]=lu(A)：

接下来我们就可以将其用于解线性方程组。

(同济线性代数P79.第16题)：若A是某个方程组的系数矩阵，并且A=

B= .

则方程组的解可以通过两次左除得到：x=U\(L\b)

MATLAB出现了如下大的信息

则说明矩阵奇异或者不可逆，这种情况下需检查矩阵是否出错或者考虑用其他方法计算。

(博主也没有学SVD分解和QR分解，这里暂时不讲，以后再补上)

6.相似矩阵与二次型：

施密特正交化：

MATLAB中正交化的指令为orth

但是MATLAB中orth指令采用的不是施密特正交，我们会在MATLAB编程中说如何自己写施密特正交。

函数eig：

matlab中求特征向量和特征值：（其中D的对角线元素为矩阵A的特征值，V的列向量是对应于特征值的特征向量。）

函数poly：

其中，若A是一个的矩阵，此函数返回的是矩阵A的特征多项式p，且p是一个n+1维的向量。

若B是一个n维向量，则函数返回的是以该向量元素为根的多项式。

函数trace：

计算函数的迹。迹是矩阵对角线元素之和。由线性代数知识我们可知：矩阵的迹等于特征值之和。

我们以线性代数p120习题为例：求矩阵 的特征值和特征向量。

下章的内容会设计到MATLAB编程，同时线性代数也会不定期更新。

机械原理大作业部分暂时还没有拟好。