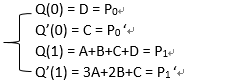前几天考了图形学考试，一开始看Hermite曲线PPT的时候不怎么看得懂，网上查资料的时候也是东一点西一点，看的头疼。本来昨天打算把关于Hermite曲线的内容整理一下，结果玩了一天回来以后就不怎么想动手，今天终于整理了。2016年来了，希望在这一年里多做一点有意义的事情。内容如下：（一开始用Word整理的，有的符号没有了，所以有的打算用截图代替）

Hermite曲线

      三次Hermite曲线是以法国数学家Charles Hermite命名的。他是三次参数样条曲线的基础。

定义：Hermite曲线是以曲线的两个端点P0，P1和端点处的切向矢量P0‘，P1‘为边界条件的三次参数曲线。

空间自由曲线三次参数方程的一般形式可表示为

现在已知P0，P1 ，P0‘，P1‘，代入求出A,B,C,D

Q’(t)=3At2+2Bt+C

解得，

A = P0 ‘+ P1 ‘+2(P0- P1)

B = 3(P1  - P0)-2 P0‘ - P1‘

C = P0 ‘

D = P0

所以，可得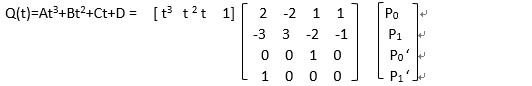

曲线可表示为Q(t) = Fn1P0+ Fn2P1 + Fn3P0‘ + Fn4P1‘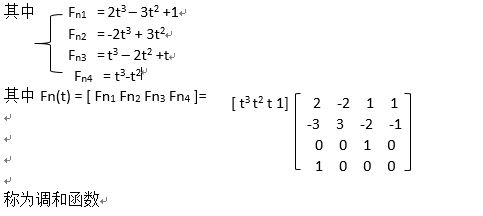

下面求Hermite的二阶导数形式：

Fn1  =2t3 – 3t2+1   F’n1 =6t2 – 6t      F’’n1 =12t - 6

Fn2  =-2t3 + 3t2      F’n2 =-6t2 + 6t     F’’n2 =-12t + 6

Fn3  =t3 – 2t2+ t    F’n3 =3t2 – 4t +1   F’’n3 =6t - 4

Fn4  = t3-t2            F’n4 = 3t2 – 2t      F’’n4 = 6t - 2

Q’’(t) = F’’n1(t)Q(0)+ F’’n2(t)Q(1) + F’’n3(t)Q’(0) + F’’n4(t)Q’(1)

t =0时：

Q’’(0) = -6Q(0) + 6Q(1) -4Q’(0) - 2Q’(1)

t =1时：

Q’’(1) = 6Q(0) - 6Q(1) +2Q’(0) + 4Q’(1)

联立消除Q’(0), Q’(1)

Q(t) = (1-t)Q(0) + tQ(1) +1/6(-t3 + 3t2 -2t)Q’’(0) + 1/6( t3-t )Q’’(1)

连续的三次参数样条曲线

现有一组离散点Pi(i = 1,2,…n)，需要构造连续曲线。据Hermite曲线的边界条件，构造n-1段曲线。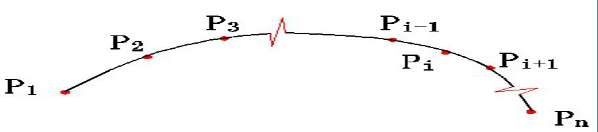

条件：连接点处，二阶导数连续

设有三点Pi-1,Pi,Pi+1构造两段曲线，即Pi-1Pi和PiPi+1

对于Pi-1Pi段：（起点）P’’i-1= -6Pi-1 + 6Pi– 4P’i-1– 2P’i

                         （终点） P’’i = 6Pi-1 -6Pi +2P’i-1 + 4P’i

对于PiPi+1段：（起点）P’’i =-6Pi + 6Pi +1– 4P’i– 2P’i+1

                         （终点） P’’i+1 = 6Pi -6Pi+1 +2P’i + 4P’i+1

得到 Pi-1+ 4Pi + Pi+1 = 3(Pi+1 - Pi-1)

边界条件分为自由端，夹持端，抛物端

1：自由端

在两端点处的二阶导数为零

即P’’1 =-6P1 + 6P2 – 4P’1 -2P’2 =0  && P’’n= 6Pn-1 – 6Pn + 2P’n-1+ 4P’n

得到 2P’1 + P’2= 3(P2 – P1)

        P’n-1 + 2P’n = 3(Pn– Pn-1)

2:夹持端

即端点处的切向矢量为已知

P’1 = k1E1     P’n = knEn   E1,En为已知的断点切向矢量

3：抛物端

即求得的分段曲线最初段和最末段为抛物线，所以曲线的二次导数为一个常数，即这两段曲线起点终点处导数相等，由此得到

P’2 + P’1= 2(P2 – P1)

P’n + P’n-1= 2(Pn – Pn-1)