[数学] 立体角 (Solid Angle) |
您所在的位置:网站首页 › angle › [数学] 立体角 (Solid Angle) |
[数学] 立体角 (Solid Angle)
|
立体角的介绍 先引用一段维基百科的介绍 立体角,常用字母Ω表示,是一个物体对特定点的三维空间的角度,是平面角在三维空间中的类比。它描述的是站在某一点的观察者测量到的物体大小的尺度。例如,对于一个特定的观察点,一个在该观察点附近的小物体有可能和一个远处的大物体有着相同的立体角。以观测点为球心,构造一个单位球面;任意物体投影到该单位球面上的投影面积,即为该物体相对于该观测点的立体角。因此,立体角是单位球面上的一块面积,这和“平面角是单位圆上的一段弧长”类似。立体角公式在球坐标系中,任意球面的极小面积为:因此,极小立体角(单位球面上的极小面积)为: \Omega ={\frac {dA}{r^{2}}}=\sin \theta \,d\theta \,d\varphi \\ 所以,立体角是投影面积与球半径平方值的比,这和“平面角是圆的弧长与半径的比”类似。 对极小立体角做曲面积分即可得立体角: \Omega =\iint _{S}d\Omega =\iint _{S}\sin \theta \,d\theta \,d\varphi \\ 封闭曲面的立体角一个完整的球面对于球内任意一点的立体角为4π sr(对于球外任意一点的立体角为0 sr): 对上面的极小立体角在整个球面上做积分: {\displaystyle \ \int _{0}^{\pi }\sin \theta d\theta \int _{0}^{2\pi }d\varphi =[-\cos \theta ]_{0}^{\pi }(2\pi )=4\pi } \\ 立体角的国际制单位是球面度(steradian,sr) 正式的介绍完了,下面来理解和推导一下。 极小立体角公式推导下面推导一下球面上的极小面积是怎么算的,先理解两个平面角。  立体角可以用两个平面角辅助表示: \theta 和 \phi ,如上图所示,\theta 是向量与垂直轴的夹角,\phi 是向量在底平面上投影向量与其中一轴的夹角。 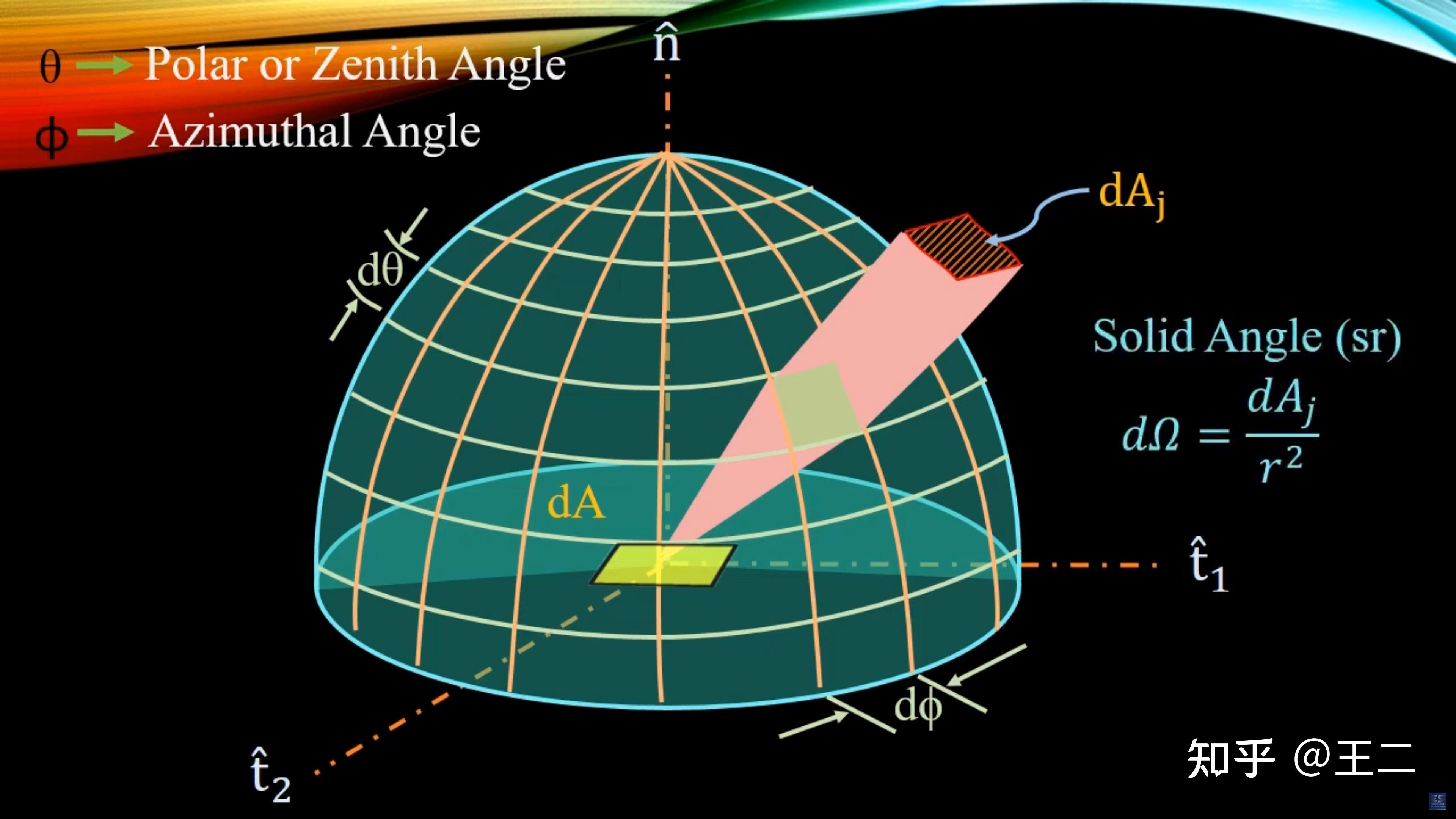 立体角公式推导-1 立体角公式推导-1如上图所示, d\phi 是立体角 \Omega 在底面上展开的平面夹角范围, d\theta 是 \Omega 与垂直轴方向的平面夹角范围,极小面积就是图中粉色锥体与球面的交面,绿色的小方形部分。  立体角公式推导-2 立体角公式推导-2如上图所示,极小面可以近似看成矩形,于是问题就变为了求矩形 ABCE 的面积 dA_{j} ,所以只要求出 AB 和 BC 两边长就可以了。 OBC 可以看作一个二维扇面,根据二维角的定义有: d\theta = \frac{\overset{\frown}{BC}}{r} \\ 于是 BC = rd\theta \tag{1} \\ BD 垂直于 n 轴,根据 \Delta OBD 有 BD = r sin\theta \tag{2} \\ 同样的 DAB 也可以看作一个二维扇面,根据二维角的定义有: d\phi=\frac{AB}{BD} \tag{3} \\ 结合 (2)(3) AB=rsin\theta\ d\phi \tag{4} \\ 结合 (1)(4) dA_{j} = AB \cdot BC=r^2sin\theta\ d\phi\ d\theta \\ 结合根据极小立体角的定义得到 \Omega ={\frac {dA_j}{r^{2}}}=\sin \theta \,d\theta \,d\varphi \\ 推导完毕。 参考: |
【本文地址】
今日新闻 |
推荐新闻 |