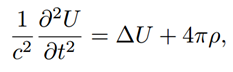7. 黎曼关于极小曲面的工作仍然被人们应用在最新的工作中: 3中的每个嵌入极小平面区域必是黎曼极小曲面、悬链曲面、螺旋曲面或者平面.

8. 黎曼对电动力学做出了深刻的贡献. 我们引用[Lau,pp. 269–270] 中的一段摘要:

······在20 世纪初期的1905 年, Einstein 和Planck 的奠基论文还未问世. 一些杰出的物理学家就把黎曼视为自己的同行. 这可以从《数学百科全书》第5 卷(物理) 的第二部分的文章中清楚地看到. 第一期出版于1904 年6 月16 日. R. Reiff 和A. Sommerfeld 的文章“远距作用的观点—— 初等定律” (第3–62 页) 中有关于Gauss 和黎曼的文字(第45 页): “Weber 是超距作用的权威, 但是径向相反趋势是由他的老师Gauss 和学生黎曼提出的······”

1858 年2 月10 日, 黎曼提交给哥廷根科学学会一篇关于电动力学的论文, 使得他成为比Maxwell 更早的电磁学先驱. 最近的电子理论, 从某种程度上, 可以追溯到黎曼的(迟滞) 初等位势.

事实上, 黎曼最早发现如下方程

······在20 世纪初期的1905 年, Einstein 和Planck 的奠基论文还未问世. 一些杰出的物理学家就把黎曼视为自己的同行. 这可以从《数学百科全书》第5 卷(物理) 的第二部分的文章中清楚地看到. 第一期出版于1904 年6 月16 日. R. Reiff 和A. Sommerfeld 的文章“远距作用的观点—— 初等定律” (第3–62 页) 中有关于Gauss 和黎曼的文字(第45 页): “Weber 是超距作用的权威, 但是径向相反趋势是由他的老师Gauss 和学生黎曼提出的······”

1858 年2 月10 日, 黎曼提交给哥廷根科学学会一篇关于电动力学的论文, 使得他成为比Maxwell 更早的电磁学先驱. 最近的电子理论, 从某种程度上, 可以追溯到黎曼的(迟滞) 初等位势.

事实上, 黎曼最早发现如下方程

其中U 和ρ 分别是位势和电荷密度. 这个方程后来也从Maxwell 理论导出. 如果c 等于光速, 黎曼的方程与经验吻合······

其中U 和ρ 分别是位势和电荷密度. 这个方程后来也从Maxwell 理论导出. 如果c 等于光速, 黎曼的方程与经验吻合······

这本书还引用了黎曼自己的话[Lau, p. 270]:

我发现电流的电动力作用可以加以解释. 前提是如果我们假设电元素的相互作用不是瞬间发生, 而是恒速传播(忽略观察的误差约等于光速). 在这个假设下, 电力微分方程和光与热辐射的传播方程一致.

我发现电流的电动力作用可以加以解释. 前提是如果我们假设电元素的相互作用不是瞬间发生, 而是恒速传播(忽略观察的误差约等于光速). 在这个假设下, 电力微分方程和光与热辐射的传播方程一致.

黎曼在1858 年作了关于电动力学的演讲, 但他的文章直到他去世后的1867 年才发表. 同时, Maxwell 在1865 年发表他的论文“电磁场的动力理论”. 我们也许可以问, Maxwell 是否知道黎曼的结果. 答案很可能是肯定的. 因为黎曼在物理学界的声望和他工作的哥廷根是物理的中心. Maxwell 也引用了两位哥廷根学者的工作: Weber 和Neumann. 他们都很接近黎曼.

11.从《黎曼全集》的前言和他人的评述看黎曼工作的影响

毫无疑问黎曼的工作对数学产生了深远而广泛的影响. 如何正确理解他的工作、发展以及影响是一个有趣的问题. 俄语版《黎曼全集》的编辑在前言中写道: 这需要一个由杰出数学家组成的团队来完成.

既然《黎曼全集》已经有了多个版本, 许多学者也撰写过黎曼工作的综述. 我们希望可以从这些不同时期的文字中, 从历史角度分析比较这些学者的观点. 希望我们的努力可以带来一个副产品: 了解数学是如何发展的.

在黎曼之后的数学家中, Klein 可以看作是黎曼最好的继承者, 至少在函数论领域. Klein 至少两次详细探讨过黎曼的工作[Kle] [Kle2].

专著[Kle] 与数学发展有关. 其中第六章讨论黎曼和Weierstrass 在函数论方面的工作. 他努力地刻画黎曼函数论和黎曼对于函数理论思想的发展. 另一方面, 他也给了一些有趣和不寻常的评论. 比如, Klein 写道:

黎曼对于他认为的典型理论之外的函数论没有太多重要的工作. 他不提及这些非黎曼的函数论及其应用. 比如黎曼zeta 函数, 因为这不能真正体现黎曼的个性, 整个步骤都属于Cauchy 的函数论.

黎曼对于他认为的典型理论之外的函数论没有太多重要的工作. 他不提及这些非黎曼的函数论及其应用. 比如黎曼zeta 函数, 因为这不能真正体现黎曼的个性, 整个步骤都属于Cauchy 的函数论.

后来, 他又评论道:

一般来说, 黎曼排斥片面性. 他总是发现任何数学都是有用的. 他寻求各种方法, 来推进和澄清他的问题.

一般来说, 黎曼排斥片面性. 他总是发现任何数学都是有用的. 他寻求各种方法, 来推进和澄清他的问题.

这也许说明Klein 区别看待黎曼创立的数学和黎曼的数学. 他的文章[Kle2] 从历史的观点强调了黎曼的工作对于数学发展的重要性.

在这两处文献中, Klein 都强调了直觉和物理经验(例如表面流体和几何工具, 黎曼面等) 对于黎曼工作的重要性. 黎曼的工作也使人们意识到这些方法的重要性. 比如Klein [Kle2, p. 169] 写道:

黎曼的在这方面的成果, 首先是使得位势理论在整个数学中变得重要. 其次, 在一系列的几何构造中······

黎曼的在这方面的成果, 首先是使得位势理论在整个数学中变得重要. 其次, 在一系列的几何构造中······

接着Klein [Kle2, p. 170] 给了一些例子:

我希望再谈一点, 黎曼从物理直觉研究数学问题所发明的新工具, 对于数学物理也有重要价值. 所以, 比如我们现在应用黎曼的方法研究二维区域中液体的稳态流. 一系列难题于是迎刃而解. 最著名的此类问题之一是Helmholtz 解决了自由液体射流的形状问题.

也许黎曼方法的一个容易被忽视的物理应用, 其中黎曼用最优美的方式处理问题, 这就是极小曲面理论······

毫无疑问, 函数论中这些方法的主要价值是他们在纯数学中的应用······

代数函数的研究与代数曲线的研究相辅相成, 后者的性质被几何学家所研究, 无论是分析几何学家(认为最重要的是解析公式), 还是综合几何学家(代表人物有Steiner 和von Staudt, 用点列与射线束作为主要工具). 黎曼所引入的新的观点是单值变换(或一一对应). 这一观点使得我们可以把不可数的代数曲线归为大类. 通过研究单独曲线形状的特殊性, 得出那些属于同一类曲线的一般性质.

我希望再谈一点, 黎曼从物理直觉研究数学问题所发明的新工具, 对于数学物理也有重要价值. 所以, 比如我们现在应用黎曼的方法研究二维区域中液体的稳态流. 一系列难题于是迎刃而解. 最著名的此类问题之一是Helmholtz 解决了自由液体射流的形状问题.

也许黎曼方法的一个容易被忽视的物理应用, 其中黎曼用最优美的方式处理问题, 这就是极小曲面理论······

毫无疑问, 函数论中这些方法的主要价值是他们在纯数学中的应用······

代数函数的研究与代数曲线的研究相辅相成, 后者的性质被几何学家所研究, 无论是分析几何学家(认为最重要的是解析公式), 还是综合几何学家(代表人物有Steiner 和von Staudt, 用点列与射线束作为主要工具). 黎曼所引入的新的观点是单值变换(或一一对应). 这一观点使得我们可以把不可数的代数曲线归为大类. 通过研究单独曲线形状的特殊性, 得出那些属于同一类曲线的一般性质.

这一观点对于黎曼面模空间的概念非常重要. Klein 为了证明紧致黎曼面的单值化定理而详细研究了模空间. 正是由于在这个问题上与Poincaré的竞争, 导致了Klein 精神崩溃. 有些令人惊讶的是, Klein 在这篇文章中没有提到黎曼模空间.

在函数论之后, Klein [Kle2, p. 175] 讨论了黎曼在微分方程上的工作:

黎曼对于复变函数论的研究, 是基于位势的偏微分方程. 他只是想把这作为一个例子, 说明所有其他的物理问题可以类似地通过偏微分方程来处理. 在每个情形, 应该了解哪些非连续性与微分方程相容, 以及方程的解在何种程度上可以从非连续性和附加条件所确定. 黎曼的这一纲领在许多方向上都取得了重要进展, 特别是近年来由法国几何学家发扬光大, 系统地重构力学和数学物理中的积分方法.

黎曼自己只用这一方法详细研究过一个问题, 就是空气中有限振幅的平面波的传播(1860 年) ······

黎曼的这篇文章从许多方面看都很杰出. 能够把这个问题归结为一个线性微分方程就是一个不小的成就. 另一个我希望引起大家关注的是对于问题的图形处理, 整篇报告都可见这一观点. 这种处理方式物理学家并不陌生, 但是其价值总是被习惯于抽象方法的数学家所低估. 所以我很高兴地指出, 黎曼常常应用这一方法, 并得到最有趣的结果.

黎曼对于复变函数论的研究, 是基于位势的偏微分方程. 他只是想把这作为一个例子, 说明所有其他的物理问题可以类似地通过偏微分方程来处理. 在每个情形, 应该了解哪些非连续性与微分方程相容, 以及方程的解在何种程度上可以从非连续性和附加条件所确定. 黎曼的这一纲领在许多方向上都取得了重要进展, 特别是近年来由法国几何学家发扬光大, 系统地重构力学和数学物理中的积分方法.

黎曼自己只用这一方法详细研究过一个问题, 就是空气中有限振幅的平面波的传播(1860 年) ······

黎曼的这篇文章从许多方面看都很杰出. 能够把这个问题归结为一个线性微分方程就是一个不小的成就. 另一个我希望引起大家关注的是对于问题的图形处理, 整篇报告都可见这一观点. 这种处理方式物理学家并不陌生, 但是其价值总是被习惯于抽象方法的数学家所低估. 所以我很高兴地指出, 黎曼常常应用这一方法, 并得到最有趣的结果.

关于黎曼的几何学基础的文章, Klein [Kle2, p. 177] 写道:

我不准备讨论其所得到的特殊几何结果和这一理论的后续发展. 我只想在此指出, 黎曼的基本思想又得到体现: 从无穷小行为解释事物的性质. 他也开创了微积分的新篇章, 即创立了任意变元的二次微分表达式理论, 特别地, 这种表达式在任意变换下的不变量理论.

我不准备讨论其所得到的特殊几何结果和这一理论的后续发展. 我只想在此指出, 黎曼的基本思想又得到体现: 从无穷小行为解释事物的性质. 他也开创了微积分的新篇章, 即创立了任意变元的二次微分表达式理论, 特别地, 这种表达式在任意变换下的不变量理论.

Klein 在最后讨论了黎曼关于三角级数的文章. 其原因是[Kle2,p. 178]:

因为这代表了黎曼想象力的一个最后的本质特征. 在所有之前的备注中, 我可以求助于物理学或者几何学当前的想法. 但是黎曼锐利的头脑不会满足于应用这些几何或物理的直觉. 他希望透彻理解这一直觉, 探讨从中得到数学结果的必要性. 这个问题类似于“无穷小微分的基本原理”. 在黎曼的其他工作中, 他从未表达过有关这一问题的确定的观点. 而这篇三角级数的文章则与众不同.

因为这代表了黎曼想象力的一个最后的本质特征. 在所有之前的备注中, 我可以求助于物理学或者几何学当前的想法. 但是黎曼锐利的头脑不会满足于应用这些几何或物理的直觉. 他希望透彻理解这一直觉, 探讨从中得到数学结果的必要性. 这个问题类似于“无穷小微分的基本原理”. 在黎曼的其他工作中, 他从未表达过有关这一问题的确定的观点. 而这篇三角级数的文章则与众不同.

《黎曼全集》的第一版出版于1876 年, 正是黎曼去世10 周年. Weber 撰写的前言没有太多评论黎曼的工作, 但提到了几个有趣而重要的事情. 比如, 黎曼关于极小曲面的文章由黎曼的学生K. Hattendorff 作了修改, 有几处较大的改动. 这来自于Weber 的要求. (参见文前插页的图片.)

Dedekind 撰写的黎曼传记也来自于Weber 的请求. 出版《黎曼全集》的一个重要原因是, 发掘黎曼未发表手稿中的宝藏. 这在今天看来依然正确. 哥廷根大学历史图书馆依然保存着上百页黎曼写过的稿纸, 其中满是复杂的计算和注记. Siegel 在1932 年发现的Riemann-Siegel 公式告诉人们在黎曼的这些草稿中还有未发掘的宝藏.

《黎曼全集》的第二版出版于16 年后的1892 年. Weber 评论了黎曼的工作在Abel 函数和线性微分方程发展中的重要性. 也许他是指Poincaré等人的工作. 他也提到高维流形和非欧几何.

第二版在1898 年被翻译成法文出版, 其中包含了Hermite 撰写的前言. Hermite 高度评价了黎曼关于Jacobi 反演问题的解答. 他也简短地讨论了代数函数分类, 黎曼面, 黎曼zeta 函数亚纯延拓的重要性. 其他黎曼的主要文章也被提及, 包括关于激波的文章. Hermite 还解释了没有详细评述的原因. 因为要解释黎曼工作的漂亮和伟大, 它们的重要性、影响和进一步发展, 需要太多的时间来完成.

《黎曼全集》的俄语版出版于1949 年. 其显著的独特之处是其中收录了编辑B. Goncharov 撰写的关于黎曼成就的详细综述, 以及点评和注释. 这是一篇非常系统和综合的关于黎曼工作的介绍, 其中包含了黎曼研究工作的发源和动机, 以及随后直到19 世纪30 年代的发展. 所以这是一份珍贵的历史资料, 让我们了解那时人们对黎曼的评价. 比如, 关于黎曼面模空间或代数方程的只有寥寥数行文字, 没有提到这方面的重要问题. 关于黎曼zeta 函数的讨论也没有解释黎曼猜想的重要性或者提及先前和当时的重要进展. (值得一提的是, 1930 年Titchmarsh 出版了他的关于黎曼zeta 函数的名著.)

《黎曼全集》的第二版在1953 年由Dover 公司重印出版, 加上了Hans Lewy 撰写的新前言, 简要概述了黎曼的主要工作, 其中提到Dirichlet 对于黎曼的影响:

黎曼的许多工作受到Dirichlet 工作特别是他的科学观的深刻影响······

黎曼的关于把函数表示成三角级数的工作正是追随并变革了Dirichlet 做出重要贡献的领域. 为此Dirichlet 与黎曼有着很好的私交.

黎曼的许多工作受到Dirichlet 工作特别是他的科学观的深刻影响······

黎曼的关于把函数表示成三角级数的工作正是追随并变革了Dirichlet 做出重要贡献的领域. 为此Dirichlet 与黎曼有着很好的私交.

Lewy 还简单提到了其他黎曼的主要文章, 并总结这些文章“都是至今仍对数学发展有着深刻影响的工作”. 他并未提及黎曼面模空间, 其真正的发展是在1953年以后.

《黎曼全集》的一个更加全面的版本由Springer 出版社在1990 年出版. 其中包含了Narasimhan 的系统介绍黎曼主要工作的长序言. 我们引用其中几段:

1. 看起来黎曼不仅预言了Hardy 和Littlewood 关于ζ 函数的最重要的发现之一, 即近似函数方程, 而且在60 年前就得到了更好的结果.

2. 黎曼为了研究函数的三角级数表示而引入的方法比其所得到的结果更有影响.

3. 黎曼坚持认为解析表达式只代表了函数的一小部分. 它的真正本质需要考虑奇点的性质和位置, 以及这个带奇点的函数所必须依赖的任意常数.

1. 看起来黎曼不仅预言了Hardy 和Littlewood 关于ζ 函数的最重要的发现之一, 即近似函数方程, 而且在60 年前就得到了更好的结果.

2. 黎曼为了研究函数的三角级数表示而引入的方法比其所得到的结果更有影响.

3. 黎曼坚持认为解析表达式只代表了函数的一小部分. 它的真正本质需要考虑奇点的性质和位置, 以及这个带奇点的函数所必须依赖的任意常数.

如今我们对黎曼模空间有很好的理解. 这个序言也讨论了黎曼模空间和Teichmüller 空间.

《黎曼全集》第二版中的大多数文章被翻译成英文由Kendrick 出版社在2004 年出版. 编辑Roger Baker (他也是《黎曼全集》的三位翻译者之一) 撰写了前言和一篇关于英文版中文章的简短摘要. 这个前言很简短, 包含了关于黎曼与Gauss, Weierstrass 和Dedekind 工作的定量比较. 其中的一些宝贵建议值得一读.

Freudenthal [Fre] 的黎曼传记很系统. 正如他指出的那样:

黎曼的风格受到哲学的影响, 包含了生涩难懂的德语语法. 不会德语的读者会很困扰. 关于黎曼工作的完整的介绍几乎没有. 只有一些肤浅的或者狂热的鼓吹文章.

黎曼的风格受到哲学的影响, 包含了生涩难懂的德语语法. 不会德语的读者会很困扰. 关于黎曼工作的完整的介绍几乎没有. 只有一些肤浅的或者狂热的鼓吹文章.

这也许是因为他受到Klein 的黎曼传记影响.

Freudenthal 强调了黎曼对于刻画全纯函数的Cauchy-Riemann 方程的欣赏. 他给了如下有趣的断言:

1. 黎曼很可能知道抽象黎曼面是具有复结构的代数簇.

2. 在黎曼的文章中零星可见一些关于高维同调的清晰想法. 其严格定义后来由Betti 和Poincaré给出.

3. 自从黎曼应用Dirichlet 原理解决Laplace 算子的边值问题以后, 人们就经常称之为Dirichlet 问题. 这完全没有道理.

4. 所有黎曼的精髓, 除了有关Dirichlet 原理的方法, 几乎都被淡忘. Theta 函数虽是热门, 但其研究并未遵循黎曼的精神. 黎曼的结果产生了巨大的影响, 但他的思考方式却鲜有追随者. 甚至解析函数的Cauchy-Riemann 定义也被放弃,Weierstrass 的幂级数定义成为主流.

5. Klein 是最早尝试复兴黎曼的复变函数几何方法的数学家. 不久, 由于Poincaré和Klein 的工作, 函数论的发展出现转机, 突破了黎曼的观点, 甚至否定黎曼最深刻的工作. 他们的工作导致自守函数理论的出现. Freudenthal 写道:

这个看似简单而显然的想法使得Jacobi 反演问题和黎曼的解答成为过眼烟云. 虽然黎曼的创新观点无处不在, 但还是过于盲从传统. 不过, 单值化和自守函数可以看作是20 世纪黎曼函数论大获成功的萌芽. 略有讽刺的是, 虽然本质上这遵循了黎曼的精神, 但还是更替甚至对立于黎曼的思想.

这个看似简单而显然的想法使得Jacobi 反演问题和黎曼的解答成为过眼烟云. 虽然黎曼的创新观点无处不在, 但还是过于盲从传统. 不过, 单值化和自守函数可以看作是20 世纪黎曼函数论大获成功的萌芽. 略有讽刺的是, 虽然本质上这遵循了黎曼的精神, 但还是更替甚至对立于黎曼的思想.

6. 如果要说黎曼有哪篇文章带给他与Abel 函数论的文章同等的声望, 那就是他关于黎曼zeta 函数的工作.

7. 黎曼对数学物理或者微分方程最重要的贡献是他发表于1860 年的关于激波的文章.

8. 在他的关于几何学基础的文章中, 数学讨论多于哲学, 不过还是对许多人的空间哲学观产生了巨大影响. 这篇文章的主要内容是用度量张量的高阶导数定义曲率. Gauss 在研究曲面时引入了曲率的概念, 并且指出曲率可以用曲面内蕴定义, 而非依赖于外围空间. 不过在Gauss 的文章中这个绝妙思想被一大堆公式所淹没.

9. 广义相对论推动了微分几何加速发展, 虽然也许更多的是量变而非质变. Freudenthal 在文章结尾引用了如下Carl Neumann 的话, 他还评论说: “也许其中隐藏了更多我们无法捉摸的智慧.”

关于几何在无限小的假定得以成立是因为度量的内在原因. 在这个问题中, 我们应该看到对离散流形而言, 度量的原理包含在流形的概念中, 而对连续流形则并非如此. 所以, 或者空间存在的实体是一个离散流形, 或者度量应该从外在发掘, 比如作用于其上的力.

关于几何在无限小的假定得以成立是因为度量的内在原因. 在这个问题中, 我们应该看到对离散流形而言, 度量的原理包含在流形的概念中, 而对连续流形则并非如此. 所以, 或者空间存在的实体是一个离散流形, 或者度量应该从外在发掘, 比如作用于其上的力.

未完待续

、、、、、1

12. 从杰出数学家们的原则来看历史上最伟大的数学家

13. 阅读《黎曼全集》的收获

参考文献

[Die] J. Dieudonne, Algebraic geometry, Advances in Math. 3 (1969) 233–321.

[Fre] H. Freudenthal, Riemann, Georg Friedrich Bernhard, Dictionary of Scientific Biography, vol. 11, 447–456, New York, 1975.

[Kle] F. Klein, Development of Mathematics in the 19th Century. With a preface and appendices by Robert Hermann. Translated from the German by M. Ackerman. Lie Groups: History, Frontiers and Applications, IX, Mathematics Sci. Press, Brookline, Mass., 1979, 175–180.

[Kle2] F. Klein, Riemann and his significance for the development of modern mathematics, Bull. Amer. Math. Soc. 1 (1895), no. 7, 165–180.

[Lau] D. Laugwitz, Bernhard Riemann 1826–1866. Turning Points in the Conception of Mathematics, Birkh¨auser Boston, Inc., Boston, MA, 2008.返回搜狐，查看更多