机器学习笔记之高斯网络(一)基本介绍 |
您所在的位置:网站首页 › 高斯-马尔可夫假设 › 机器学习笔记之高斯网络(一)基本介绍 |
机器学习笔记之高斯网络(一)基本介绍
|
机器学习笔记之高斯网络——基本介绍
引言回顾:条件独立性概率图模型
高斯网络高斯网络介绍高斯网络的条件独立性随机变量之间的边缘独立随机变量之间的条件独立
引言
本节将介绍高斯网络 回顾: 条件独立性在概率图模型——背景介绍中介绍了条件独立性,条件独立性的核心思想是:给定某随机变量集合 X A \mathcal X_{\mathcal A} XA的条件下,可能存在随机变量集合 X B , X C \mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XB,XC内部结点之间存在关联,但 X B , X C \mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XB,XC之间不存在关联: X B ⊥ X C ∣ X A \mathcal X_{\mathcal B} \perp \mathcal X_{\mathcal C} \mid \mathcal X_{\mathcal A} XB⊥XC∣XA 并且 X A , X B , X C \mathcal X_{\mathcal A},\mathcal X_{\mathcal B},\mathcal X_{\mathcal C} XA,XB,XC是三个不相交的特征集合。 概率图模型在概率图模型——背景介绍中介绍了概率图模型(Probabilisitc Graphical Model,PGM)。从图的表示角度观察,它可以分为有向图和无向图两种: 基于有向图的概率图模型又称贝叶斯网络(Bayesian Network),也称信念网络(Belief Network)。 从条件独立性的角度观察,贝叶斯网络的条件独立性表达包含三种经典情况: 同父结构(Common Parent),对应概率图结构表示如下: 上图结构表现的现象是:给定结点
i
1
i_1
i1的取值,结点
i
2
,
i
3
i_2,i_3
i2,i3条件独立。
i
2
⊥
i
3
∣
i
1
i_2 \perp i_3 \mid i_1
i2⊥i3∣i1顺序结构(Sequence),对应概率图结构表示如下: 上图结构表现的现象是:给定结点
i
1
i_1
i1的取值,结点
i
2
,
i
3
i_2,i_3
i2,i3条件独立。
i
2
⊥
i
3
∣
i
1
i_2 \perp i_3 \mid i_1
i2⊥i3∣i1顺序结构(Sequence),对应概率图结构表示如下: 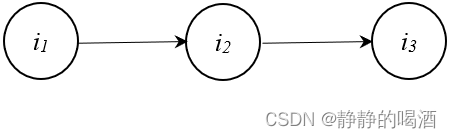 上图结构表现的现象是:给定结点
i
2
i_2
i2的取值,结点
i
1
,
i
3
i_1,i_3
i1,i3相互独立。
i
1
⊥
i
3
∣
i
2
i_1 \perp i_3 \mid i_2
i1⊥i3∣i2
V
\mathcal V
V型结构(V-Structure),对应概率图结构表示如下: 上图结构表现的现象是:给定结点
i
2
i_2
i2的取值,结点
i
1
,
i
3
i_1,i_3
i1,i3相互独立。
i
1
⊥
i
3
∣
i
2
i_1 \perp i_3 \mid i_2
i1⊥i3∣i2
V
\mathcal V
V型结构(V-Structure),对应概率图结构表示如下: 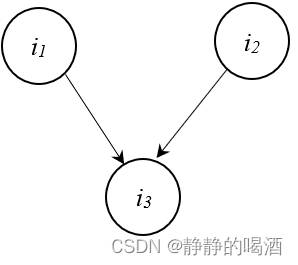 该结构表现的现象是:给定
i
3
i_3
i3结点的条件下,
i
1
,
i
2
i_1,i_2
i1,i2必不独立;相反,
i
3
i_3
i3取值未知的条件下,
i
1
,
i
2
i_1,i_2
i1,i2相互独立。
i
3
∣
i
1
⊥
i
2
i_3 \mid i_1 \perp i_2
i3∣i1⊥i2 该结构表现的现象是:给定
i
3
i_3
i3结点的条件下,
i
1
,
i
2
i_1,i_2
i1,i2必不独立;相反,
i
3
i_3
i3取值未知的条件下,
i
1
,
i
2
i_1,i_2
i1,i2相互独立。
i
3
∣
i
1
⊥
i
2
i_3 \mid i_1 \perp i_2
i3∣i1⊥i2 基于无向图的概率图模型又称马尔可夫网络(Markov Network),也称马尔可夫随机场(Markov Random Field)。 相比于贝叶斯网络,马尔可夫随机场中描述变量之间的依赖关系 仅包含一种格式: 高斯网络(Gaussian Network),又称高斯概率图模型(Gaussian Probabilistic Graphical Model)。它同样也是一种概率图模型。 从随机变量的类型角度观察,将随机变量分为离散型随机变量核连续型随机变量两种。已经介绍的随机变量是离散型随机变量的有: 高斯混合模型(Gaussian Mixture Model,GMM),其隐变量 Z \mathcal Z Z包含离散的 ∣ K ∣ |\mathcal K| ∣K∣个取值,每个取值条件下的观测变量服从高斯分布: P ( X ) = ∑ k = 1 K α k ⋅ N ( μ k , Σ k ) ∑ k = 1 K α k = 1 \mathcal P(\mathcal X) = \sum_{k=1}^{\mathcal K} \alpha_k \cdot \mathcal N(\mu_{k},\Sigma_k) \quad \sum_{k=1}^{\mathcal K} \alpha_k = 1 P(X)=k=1∑Kαk⋅N(μk,Σk)k=1∑Kαk=1隐马尔可夫模型(Hidden Markov Model,HMM):隐变量 I \mathcal I I是离散型随机变量,观测变量 O \mathcal O O没有要求。条件随机场(Condition Random Field,CRF):隐变量 I \mathcal I I是离散型随机变量,观测变量 O 1 : T \mathcal O_{1:T} O1:T常以序列形式出现。而高斯网络是随机变量是连续型随机变量 的一种代表模型,其核心思想是:随机变量都是连续型随机变量,并且随机变量服从高斯分布。同上,根据图的表示,高斯网络同样分为有向图和无向图两种表达形式: 高斯贝叶斯网络(Gaussian Beyasian Network,GBN)高斯马尔可夫网络(Gaussian Markov Network,GMN) 高斯网络的条件独立性假设一个高斯图模型表示如下: 根据协方差的定义,如果在同一物理量纲(基准)的条件下, C o v ( x i , x j ) = 0 Cov(x_i,x_j) = 0 Cov(xi,xj)=0,那个称随机变量 x i , x j x_i,x_j xi,xj是不相关的。从独立性的角度观察,即 x i , x j x_i,x_j xi,xj相互独立: 这个相互独立意味着 x i x_i xi和 x j x_j xj在不观察其他变量的条件下是‘边缘独立/绝对独立’的,这种独立在现实世界的问题中并不常见。 σ i j = 0 ⇒ x i ⊥ x j σ i j = 0 ⇒ P ( x i , x j ) = P ( x i ) P ( x j ) \begin{aligned} \sigma_{ij} = 0 & \Rightarrow x_i \perp x_j \\ \sigma_{ij} = 0 & \Rightarrow \mathcal P(x_i,x_j) = \mathcal P(x_i)\mathcal P(x_j) \end{aligned} σij=0σij=0⇒xi⊥xj⇒P(xi,xj)=P(xi)P(xj) 如果两个随机变量之间的基准存在差异,对应的 σ i j \sigma_{ij} σij也可能存在很大差异。为此可以引入相关系数(Correlation Coefficient): ρ i j = C o v ( x i , x j ) D ( x i ) D ( x j ) = σ i j σ i i σ j j \begin{aligned} \rho_{ij} & = \frac{Cov(x_i,x_j)}{\sqrt{\mathcal D(x_i)}\sqrt{\mathcal D(x_j)}} \\ & = \frac{\sigma_{ij}}{\sqrt{\sigma_{ii}\sigma_{jj}}} \end{aligned} ρij=D(xi) D(xj) Cov(xi,xj)=σiiσjj σij 如果相关系数 ρ i j = 0 \rho_{ij} = 0 ρij=0称 x i , x j x_i,x_j xi,xj不相关。 随机变量之间的条件独立条件独立性本质上是为了简化运算提出的一种假设,从而在概率图模型中得到映射。 关于高斯网络的条件独立性,引入一个概念:精度矩阵(Precision Matrix),也称作 信息矩阵(Information Matrix)。它是协方差矩阵的逆矩阵: 第一次遇到‘精度矩阵’是在推断任务之边缘概率分布与条件概率分布,记录一下时间点~ Λ = Σ − 1 = ( λ 11 , λ 12 , ⋯ , λ 1 p λ 21 , λ 22 , ⋯ , λ 2 p ⋮ λ p 1 , λ p 2 , ⋯ , λ p p ) p × p \Lambda = \Sigma^{-1} = \begin{pmatrix} \lambda_{11},\lambda_{12},\cdots,\lambda_{1p} \\ \lambda_{21},\lambda_{22},\cdots,\lambda_{2p} \\ \vdots \\ \lambda_{p1},\lambda_{p2},\cdots,\lambda_{pp} \\ \end{pmatrix}_{p \times p} Λ=Σ−1=⎝⎜⎜⎜⎛λ11,λ12,⋯,λ1pλ21,λ22,⋯,λ2p⋮λp1,λp2,⋯,λpp⎠⎟⎟⎟⎞p×p 关于精度矩阵 Λ \Lambda Λ与条件独立性的关联关系表示如下: 其中 x − i − j x_{-i-j} x−i−j表示随机变量集合 X \mathcal X X中除去 x i , x j x_i,x_j xi,xj之外的其他随机变量。 λ i j = 0 ⇔ x i ⊥ x j ∣ x − i − j \lambda_{ij} = 0 \Leftrightarrow x_i \perp x_j \mid x_{-i-j} λij=0⇔xi⊥xj∣x−i−j 精度矩阵的核心在于:精度矩阵中的元素与条件独立性(概率图的映射)紧密结合在一起。 下一节将介绍高斯贝叶斯网络。 相关参考: 高斯图模型、精度矩阵、偏相关系数、贝叶斯估计(利用贝叶斯做数据融合)、Wishart分布和逆Wishart分布 协方差——百度百科 概率图模型(四):经典概率图模型 机器学习-高斯网络(1)-总体介绍 |
【本文地址】
今日新闻 |
推荐新闻 |
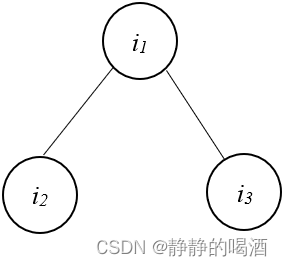 该结构表现的现象是:给定
i
1
i_1
i1结点的条件下,结点
i
2
,
i
3
i_2,i_3
i2,i3相互独立。
i
2
⊥
i
3
∣
i
1
i_2 \perp i_3 \mid i_1
i2⊥i3∣i1
该结构表现的现象是:给定
i
1
i_1
i1结点的条件下,结点
i
2
,
i
3
i_2,i_3
i2,i3相互独立。
i
2
⊥
i
3
∣
i
1
i_2 \perp i_3 \mid i_1
i2⊥i3∣i1 这只是一个简单的马尔可夫网络,并且每个结点都是一个一维随机变量。这里的随机变量均是连续型随机变量,并且均服从高斯分布:
x
i
∼
N
(
μ
i
,
Σ
i
)
x_i \sim \mathcal N(\mu_i,\Sigma_i)
xi∼N(μi,Σi) 假设随机变量集合的维数是
p
p
p,整个高斯图模型中所有随机变量对应的概率密度函数
P
(
X
)
\mathcal P(\mathcal X)
P(X)表示为:
X
=
(
x
1
,
x
2
,
⋯
,
x
p
)
T
P
(
X
)
=
1
(
2
π
)
p
2
∣
Σ
∣
1
2
exp
[
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
]
\begin{aligned} \mathcal X & = (x_1,x_2,\cdots,x_p)^T \\ \mathcal P(\mathcal X) & = \frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left[-\frac{1}{2} (x - \mu)^T \Sigma^{-1}(x - \mu)\right] \end{aligned}
XP(X)=(x1,x2,⋯,xp)T=(2π)2p∣Σ∣211exp[−21(x−μ)TΣ−1(x−μ)] 这明显是一个多元高斯分布。一个高斯图模型和一个多元高斯分布存在映射关系。其中
μ
\mu
μ表示多元高斯分布的期望,
Σ
\Sigma
Σ表示多元高斯分布的协方差矩阵。 其中,期望
μ
\mu
μ表示为:
μ
=
[
μ
i
]
p
×
1
=
(
μ
1
μ
2
⋮
μ
p
)
p
×
1
\mu = [\mu_i]_{p \times 1} = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_p \end{pmatrix}_{p \times 1}
μ=[μi]p×1=⎝⎜⎜⎜⎛μ1μ2⋮μp⎠⎟⎟⎟⎞p×1 协方差矩阵
Σ
\Sigma
Σ表示为:
Σ
=
[
σ
i
j
]
p
×
p
=
(
σ
11
,
σ
12
,
⋯
,
σ
1
p
σ
21
,
σ
22
,
⋯
,
σ
2
p
⋮
σ
p
1
,
σ
p
2
,
⋯
,
σ
p
p
)
p
×
p
\Sigma = [\sigma_{ij}]_{p \times p} = \begin{pmatrix} \sigma_{11},\sigma_{12},\cdots,\sigma_{1p} \\ \sigma_{21},\sigma_{22},\cdots,\sigma_{2p} \\ \vdots \\ \sigma_{p1},\sigma_{p2},\cdots,\sigma_{pp} \\ \end{pmatrix}_{p \times p}
Σ=[σij]p×p=⎝⎜⎜⎜⎛σ11,σ12,⋯,σ1pσ21,σ22,⋯,σ2p⋮σp1,σp2,⋯,σpp⎠⎟⎟⎟⎞p×p 其中
σ
i
j
\sigma_{ij}
σij表示随机变量
x
i
,
x
j
x_i,x_j
xi,xj的协方差结果: 这里没有写成
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
T
(x_i - \mu_i)(x_j - \mu_j)^T
(xi−μi)(xj−μj)T因为已经设定的一维随机变量。
σ
i
j
=
C
o
v
(
x
i
,
x
j
)
=
E
[
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
]
\sigma_{ij} = Cov(x_i,x_j) = \mathbb E\left[(x_i - \mu_i)(x_j - \mu_j)\right]
σij=Cov(xi,xj)=E[(xi−μi)(xj−μj)]
这只是一个简单的马尔可夫网络,并且每个结点都是一个一维随机变量。这里的随机变量均是连续型随机变量,并且均服从高斯分布:
x
i
∼
N
(
μ
i
,
Σ
i
)
x_i \sim \mathcal N(\mu_i,\Sigma_i)
xi∼N(μi,Σi) 假设随机变量集合的维数是
p
p
p,整个高斯图模型中所有随机变量对应的概率密度函数
P
(
X
)
\mathcal P(\mathcal X)
P(X)表示为:
X
=
(
x
1
,
x
2
,
⋯
,
x
p
)
T
P
(
X
)
=
1
(
2
π
)
p
2
∣
Σ
∣
1
2
exp
[
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
]
\begin{aligned} \mathcal X & = (x_1,x_2,\cdots,x_p)^T \\ \mathcal P(\mathcal X) & = \frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}} \exp \left[-\frac{1}{2} (x - \mu)^T \Sigma^{-1}(x - \mu)\right] \end{aligned}
XP(X)=(x1,x2,⋯,xp)T=(2π)2p∣Σ∣211exp[−21(x−μ)TΣ−1(x−μ)] 这明显是一个多元高斯分布。一个高斯图模型和一个多元高斯分布存在映射关系。其中
μ
\mu
μ表示多元高斯分布的期望,
Σ
\Sigma
Σ表示多元高斯分布的协方差矩阵。 其中,期望
μ
\mu
μ表示为:
μ
=
[
μ
i
]
p
×
1
=
(
μ
1
μ
2
⋮
μ
p
)
p
×
1
\mu = [\mu_i]_{p \times 1} = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_p \end{pmatrix}_{p \times 1}
μ=[μi]p×1=⎝⎜⎜⎜⎛μ1μ2⋮μp⎠⎟⎟⎟⎞p×1 协方差矩阵
Σ
\Sigma
Σ表示为:
Σ
=
[
σ
i
j
]
p
×
p
=
(
σ
11
,
σ
12
,
⋯
,
σ
1
p
σ
21
,
σ
22
,
⋯
,
σ
2
p
⋮
σ
p
1
,
σ
p
2
,
⋯
,
σ
p
p
)
p
×
p
\Sigma = [\sigma_{ij}]_{p \times p} = \begin{pmatrix} \sigma_{11},\sigma_{12},\cdots,\sigma_{1p} \\ \sigma_{21},\sigma_{22},\cdots,\sigma_{2p} \\ \vdots \\ \sigma_{p1},\sigma_{p2},\cdots,\sigma_{pp} \\ \end{pmatrix}_{p \times p}
Σ=[σij]p×p=⎝⎜⎜⎜⎛σ11,σ12,⋯,σ1pσ21,σ22,⋯,σ2p⋮σp1,σp2,⋯,σpp⎠⎟⎟⎟⎞p×p 其中
σ
i
j
\sigma_{ij}
σij表示随机变量
x
i
,
x
j
x_i,x_j
xi,xj的协方差结果: 这里没有写成
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
T
(x_i - \mu_i)(x_j - \mu_j)^T
(xi−μi)(xj−μj)T因为已经设定的一维随机变量。
σ
i
j
=
C
o
v
(
x
i
,
x
j
)
=
E
[
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
]
\sigma_{ij} = Cov(x_i,x_j) = \mathbb E\left[(x_i - \mu_i)(x_j - \mu_j)\right]
σij=Cov(xi,xj)=E[(xi−μi)(xj−μj)]