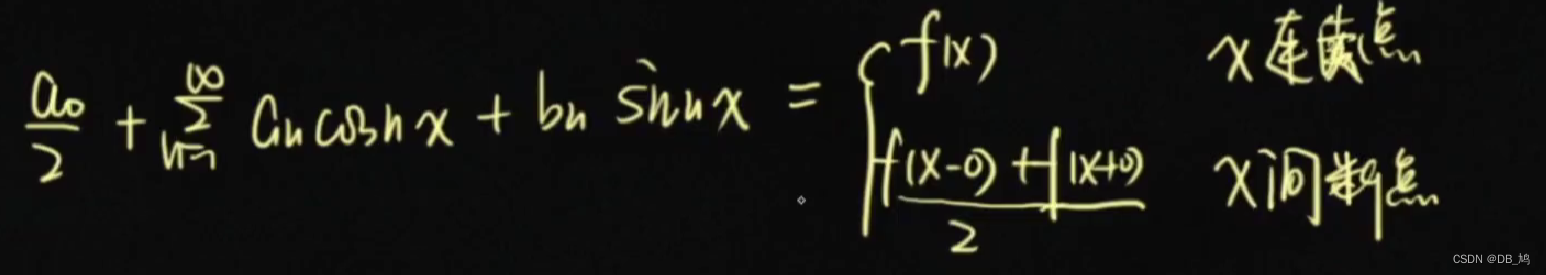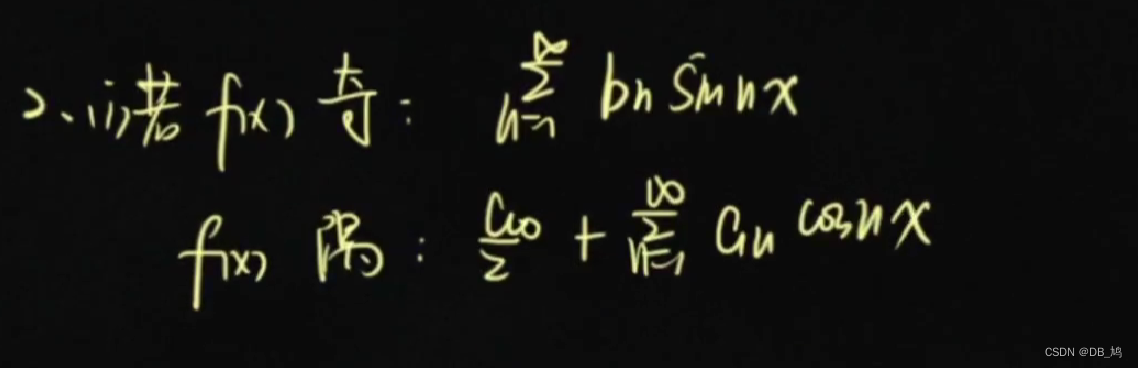高数 |
您所在的位置:网站首页 › 高数都是什么内容 › 高数 |
高数
|
常数项级数
定义
先搞清什么是级数,级数是一个求和,可以先理解为是数列的求和。 这样一个级数: ∑ n = 1 ∞ f ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( n ) + . . . \sum_{n=1}^\infty f(n) = f(1) + f(2) + f(3) + ... + f(n) + ... ∑n=1∞f(n)=f(1)+f(2)+f(3)+...+f(n)+... S ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( n ) S(n) = f(1) + f(2) + f(3) + ... + f(n) S(n)=f(1)+f(2)+f(3)+...+f(n) 叫做部分和 如果 lim n → ∞ S ( n ) = S ( 常数 ) \lim\limits_{n\to\infty} S(n) = S(常数) n→∞limS(n)=S(常数),那么级数收敛。 使用定义法判断敛散性要学会的计算方法 数列求和求极限 性质 如果 ∑ n = 1 ∞ f ( n ) = S \sum_{n=1}^\infty f(n) = S ∑n=1∞f(n)=S ,则 ∑ n = 1 ∞ k f ( n ) = k S \sum_{n=1}^\infty kf(n) = kS ∑n=1∞kf(n)=kS如果 ∑ n = 1 ∞ f 1 ( n ) = S 1 , ∑ n = 1 ∞ f 2 ( n ) = S 2 \sum_{n=1}^\infty f1(n) = S1,\sum_{n=1}^\infty f2(n) = S2 ∑n=1∞f1(n)=S1,∑n=1∞f2(n)=S2 ,则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) = S 1 + S 2 \sum_{n=1}^\infty f1(n)+f2(n) = S1+S2 ∑n=1∞f1(n)+f2(n)=S1+S2如果 ∑ n = 1 ∞ f 1 ( n ) 收敛, ∑ n = 1 ∞ f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n) 收敛,\sum_{n=1}^\infty f2(n) 发散 ∑n=1∞f1(n)收敛,∑n=1∞f2(n)发散 ,则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n)+f2(n) 发散 ∑n=1∞f1(n)+f2(n)发散如果 ∑ n = 1 ∞ f 1 ( n ) 发散, ∑ n = 1 ∞ f 2 ( n ) 发散 \sum_{n=1}^\infty f1(n) 发散,\sum_{n=1}^\infty f2(n) 发散 ∑n=1∞f1(n)发散,∑n=1∞f2(n)发散 ,则 ∑ n = 1 ∞ f 1 ( n ) + f 2 ( n ) 收敛性不确定 \sum_{n=1}^\infty f1(n)+f2(n) 收敛性不确定 ∑n=1∞f1(n)+f2(n)收敛性不确定如果 ∑ n = 1 ∞ f ( n ) 收敛 \sum_{n=1}^\infty f(n) 收敛 ∑n=1∞f(n)收敛 ,则 lim n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞limf(n)=0如果 lim n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞limf(n)=0,不一定 ∑ n = 1 ∞ f ( n ) 收敛 \sum_{n=1}^\infty f(n) 收敛 ∑n=1∞f(n)收敛如果 lim n → ∞ f ( n ) ≠ 0 \lim\limits_{n\to\infty} f(n) \not= 0 n→∞limf(n)=0,则 ∑ n = 1 ∞ f ( n ) 发散 \sum_{n=1}^\infty f(n) 发散 ∑n=1∞f(n)发散 常用级数的敛散性
级数中的每一项都大于0的叫做正项级数。 比较法 大级数收敛,则小级数收敛小级数发散,则大级数发散两个级数的比值为常数(0, + ∞ +\infty +∞),则两个级数的敛散性相同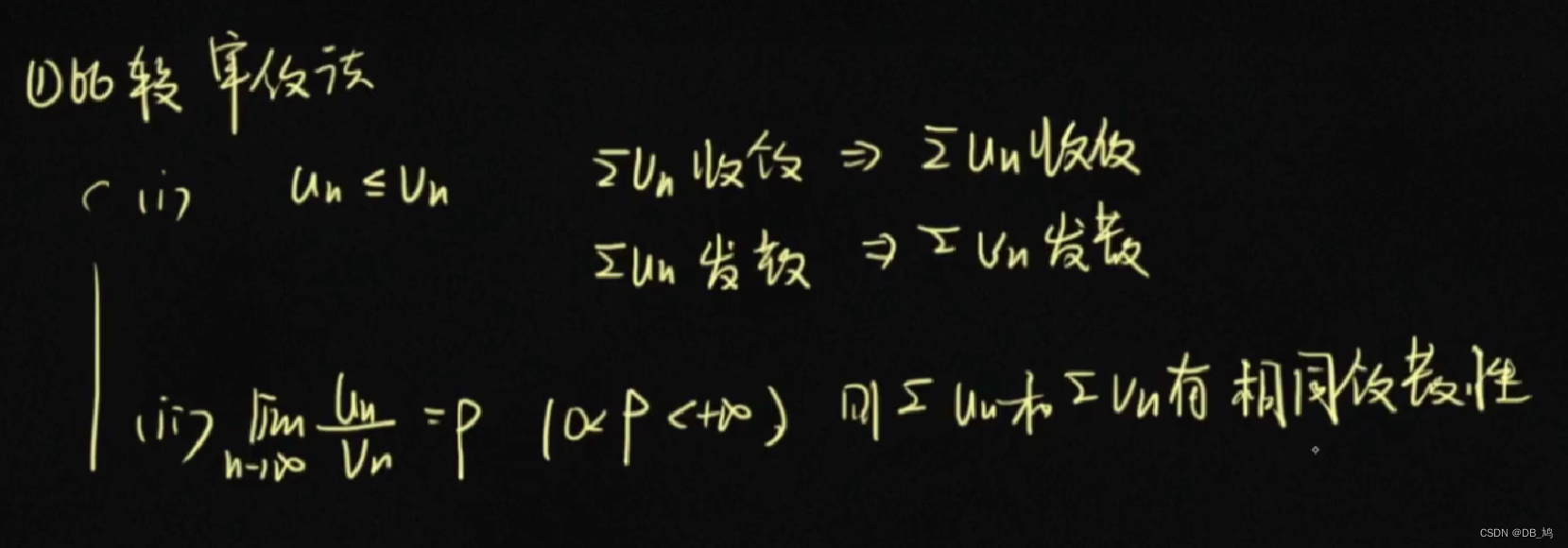 比值法
比值法
当n趋向无穷大时,有后一项与前一项比较得出一个数s。 如果s小于1,则级数收敛; 若s大于1,则级数发散。  利用性质7、常用级数和比较法 利用性质7、常用级数和比较法 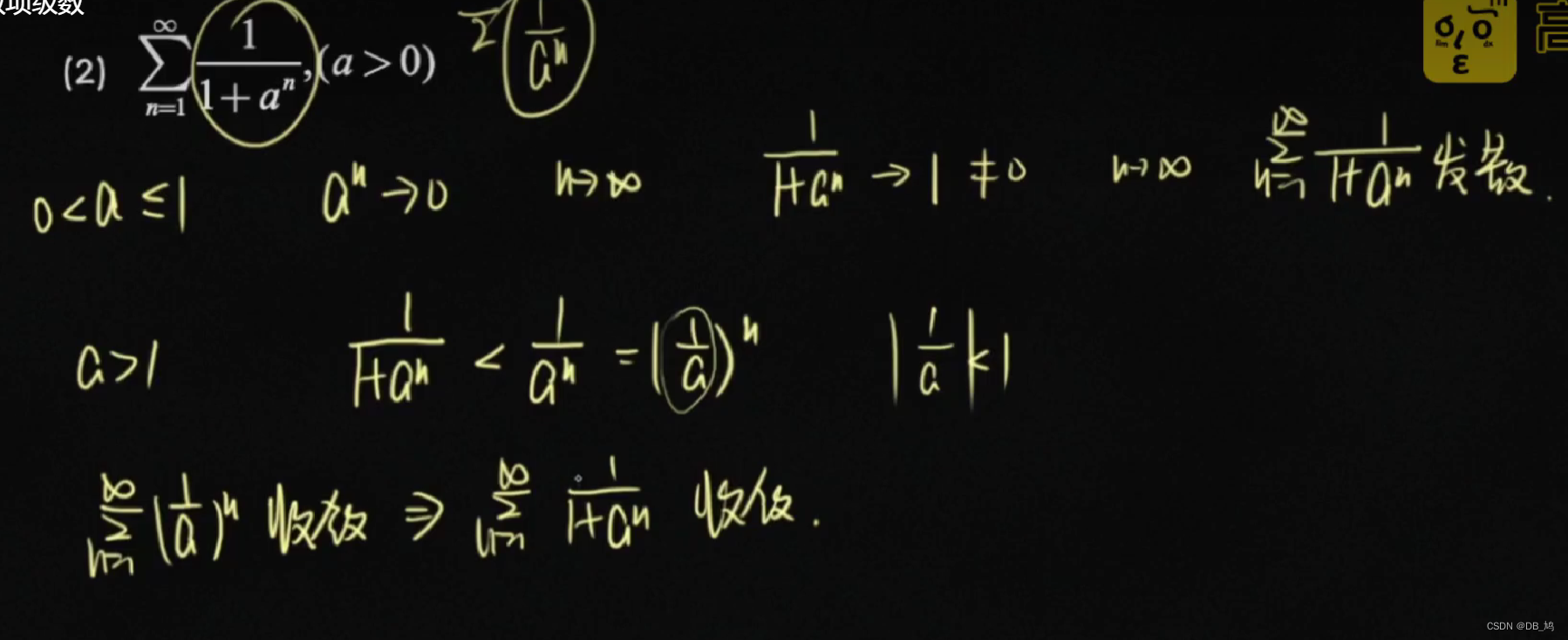 比值法 比值法  比值法 比值法 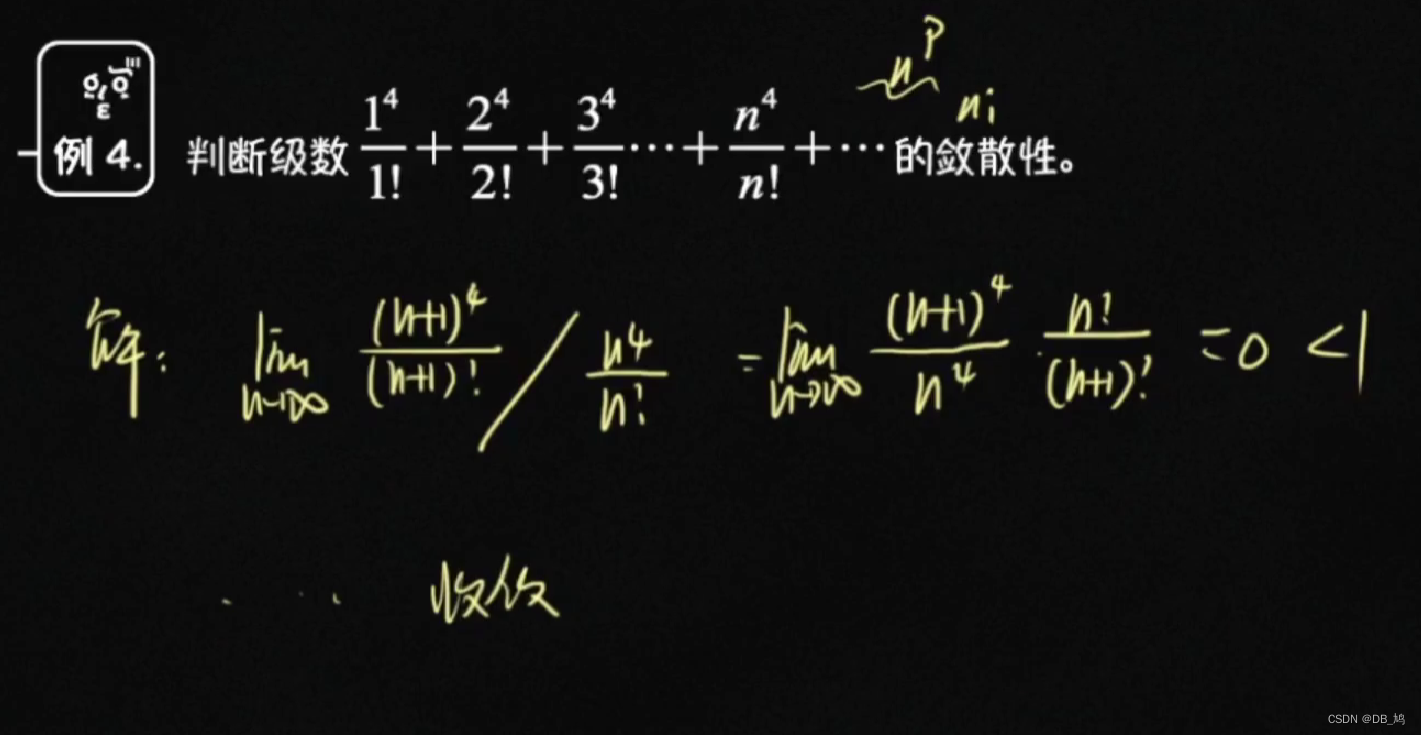 交错级数审敛法
交错级数审敛法
级数中各项为正负交错称为交错级数 莱布尼兹定理使用莱布尼兹定理: 对于这样一个级数: f ( n ) = ( − 1 ) − 1 u ( n ) f(n) =(-1)^{-1}u(n) f(n)=(−1)−1u(n) 在不考虑符号的情况下,u(n)单调递减且 lim n → ∞ f ( n ) = 0 \lim\limits_{n\to\infty} f(n) = 0 n→∞limf(n)=0,则交错级数收敛 绝对收敛和条件收敛在级数收敛的前提下分为绝对收敛和条件收敛 如果级数的公式加绝对值后求级数依然收敛,那么称为绝对收敛。 如果加绝对值之后变为发散,则称为条件收敛。 例题
解题过程 先判断是不是绝对收敛判断是不是条件收敛都不是就是发散的
常数项级数的每一项都是函数,幂级数的每一项都是函数,一般都是幂函数,所以称为幂级数。 ∑ n = 1 ∞ f n ( x ) = a n ( x − x 0 ) n \sum_{n=1}^\infty f_n(x) = a_n(x-x_0)^n ∑n=1∞fn(x)=an(x−x0)n 收敛半径、收敛区间、收敛域 收敛半径: R = lim n → ∞ ∣ a n a n + 1 ∣ R = \lim\limits_{n\to\infty} | \frac{a_n}{a_{n+1}}| R=n→∞lim∣an+1an∣收敛区间: ( − R , R ) (-R,R) (−R,R)收敛域:讨论当x = ± R \pm R ±R时对应的常数项级数的敛散性,收敛这则一端为闭区间,发散则这一端为开区间例题 求和的结果称为和函数 重要的公式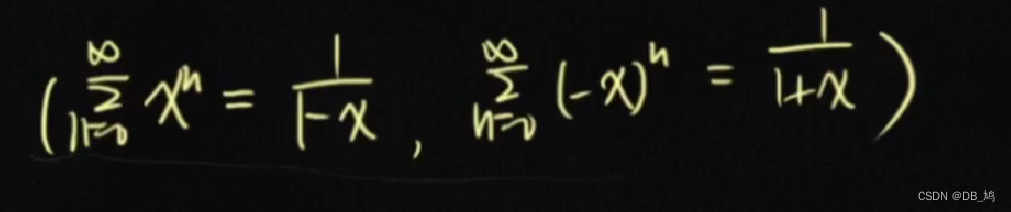 求解方法:代数变换、求导和积分 求解方法:代数变换、求导和积分  例题 例题
记得先求收敛域,收敛域就是和函数的定义域
进行适当的代数变换
直接法:公式法 间接法:傅里叶展开 例题 展开公式
|
【本文地址】
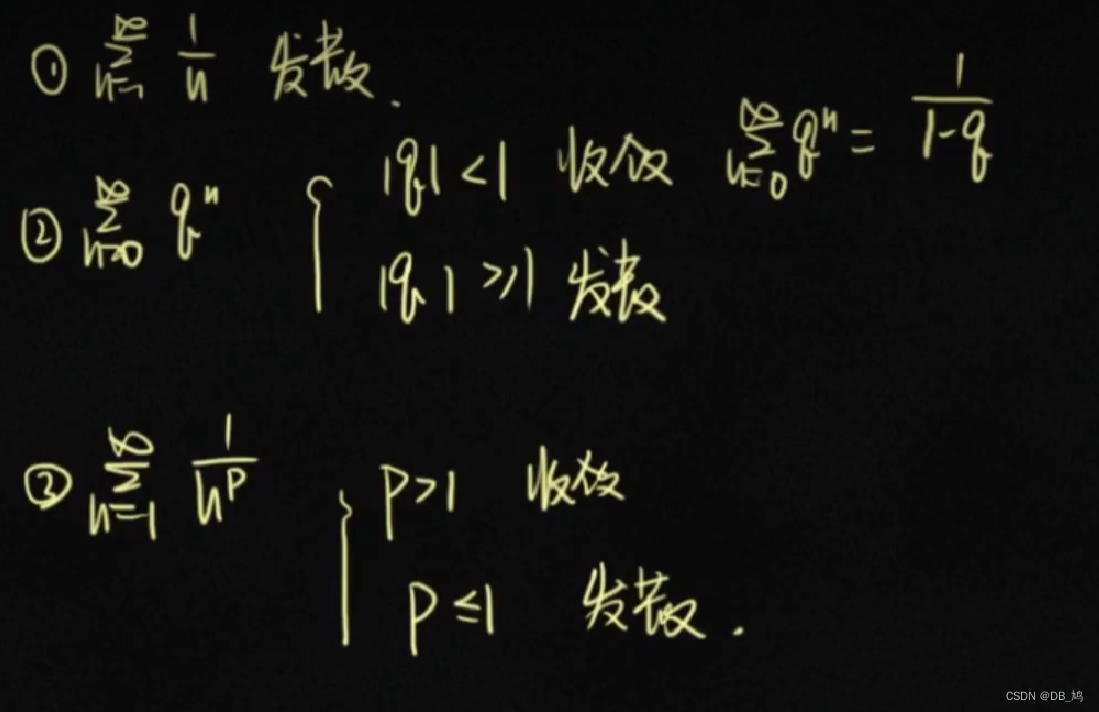
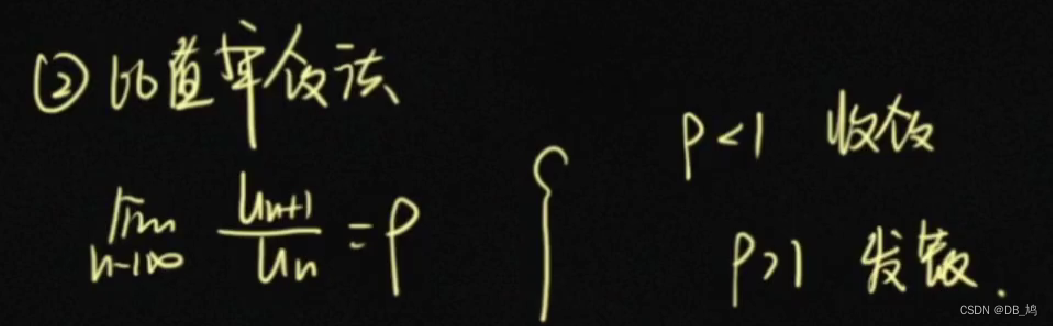




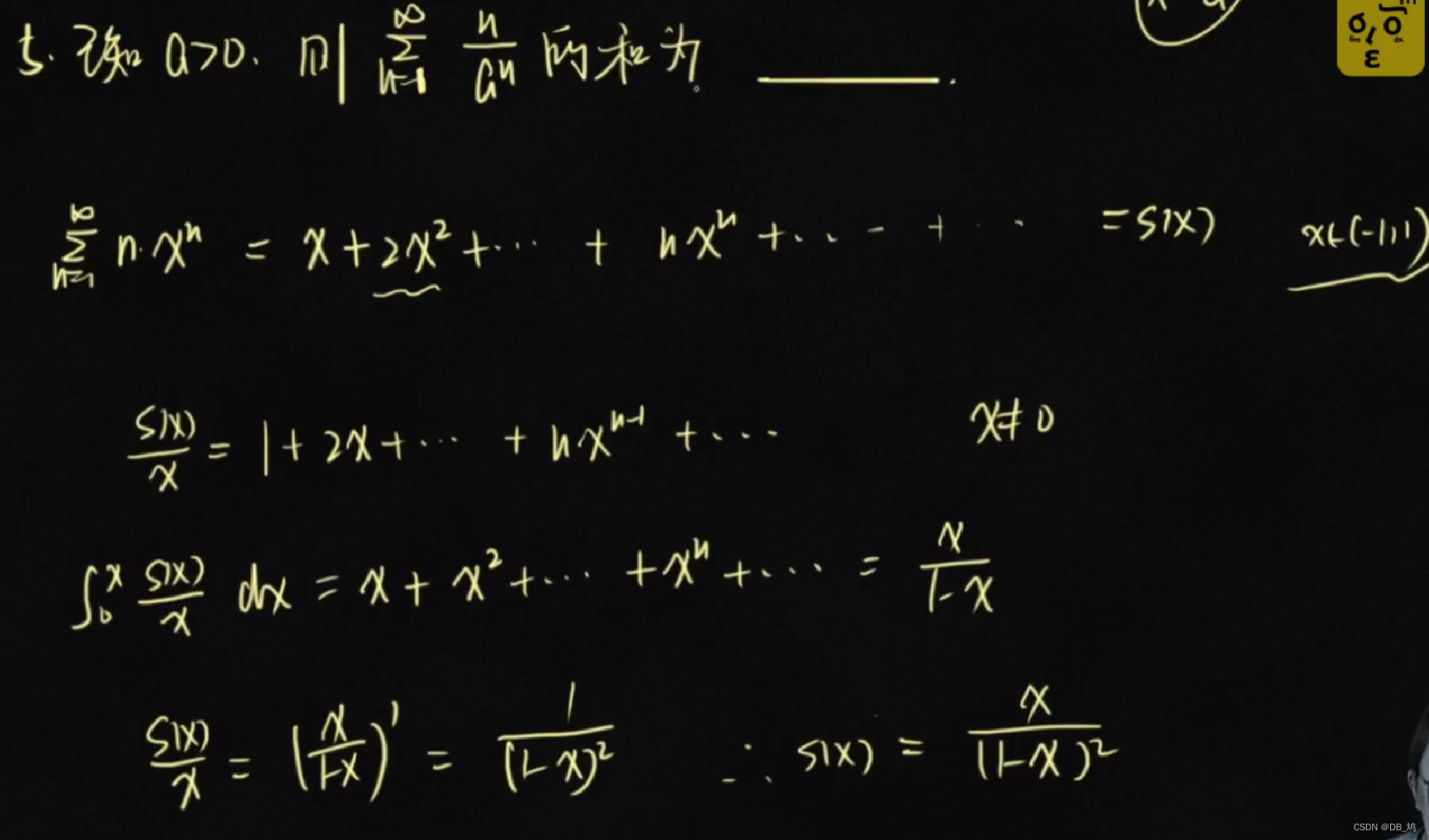
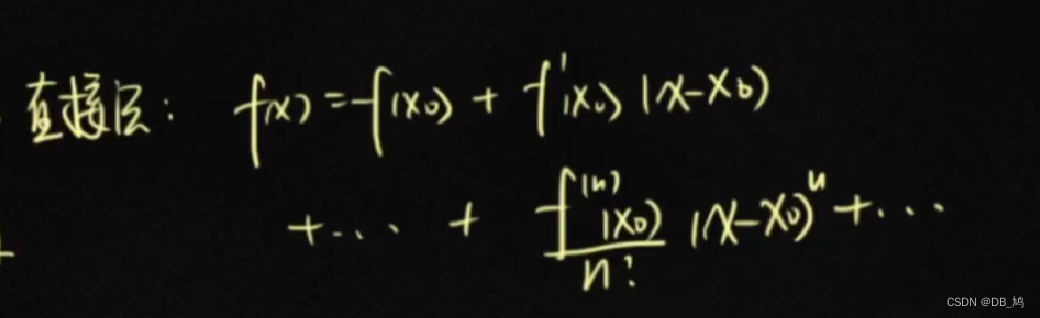


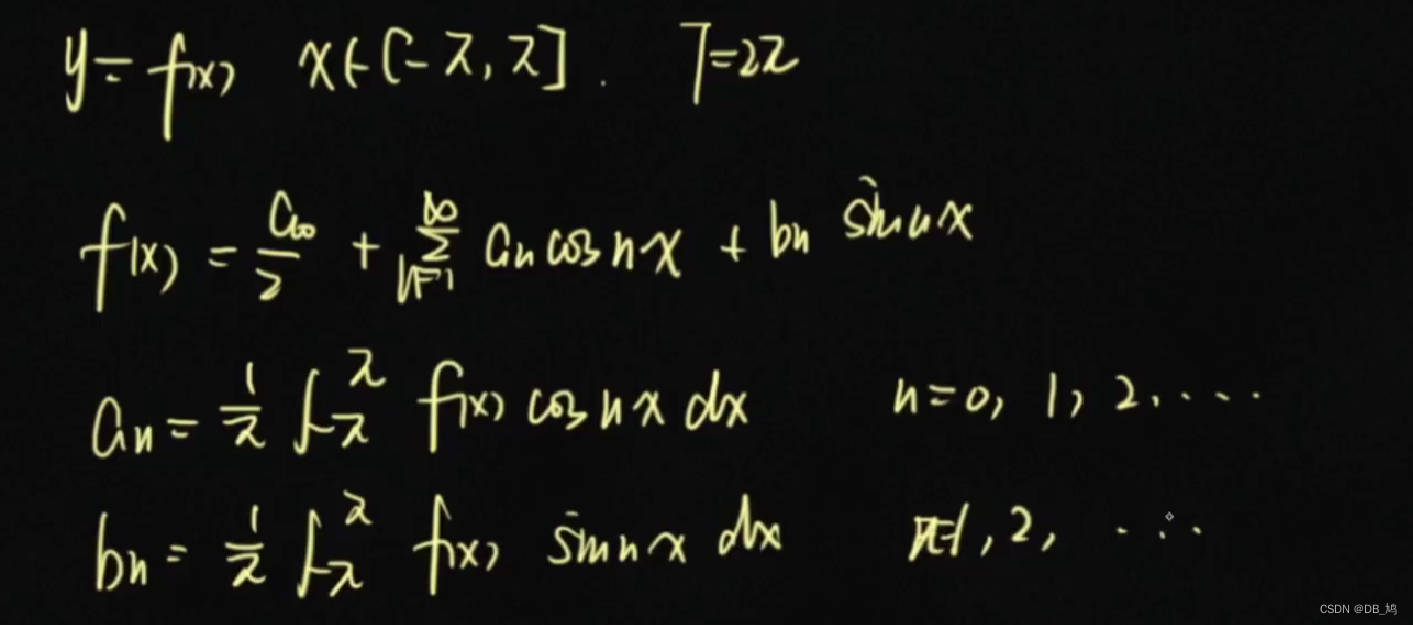 求和公式
求和公式