动态规划之马拉车算法(Python解法) |
您所在的位置:网站首页 › 马拉车什么品牌 › 动态规划之马拉车算法(Python解法) |
动态规划之马拉车算法(Python解法)
|
问题描述:
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。如"abc"有三个回文子串‘a','b','c'. 示例 1: 输入:"abc" 输出:3 解释:三个回文子串: "a", "b", "c" 示例 2: 输入:"aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa" 对于这个问题,简单的思路是枚举字符串中的每个子串,然后判断子串中回文串的个数。O(N^3) 本篇文章主要介绍我个人对马拉车算法实现思路的一些想法,原题解请看leetcode-647.回文子串 中心拓展法 由于回文串有对称性这一特点,每个回文串必然存在一个对称中心。我们可以对字符串中每个字符或两个字符之间的位置(若回文串长度为偶数)当作对称中心进行枚举,例如s="abcba",当i=2时,判断a[1]==a[3],a[0]==a[4].....如果左右两边字符相同时则继续扩展,一旦不相同则更新最大扩展长度并退出当前循环,继续枚举下一个对称中心。 假设字符串的长度为 n,枚举每个对称中心(长度为 1 和 0的对称中心分别有 n 和 n-1 个),共遍历2n-1次,时间复杂度为 O(n);每个对称中心最多向外拓展n次,所以整体的时间复杂度是 O(n^2)。空间复杂度为O(1)。 代码如下(直接抄leetcode了): //遍历2n-1次,就能够得到所有可能的对称中心 for (int i = 0; i < 2 * n - 1; i++) { int l = i / 2, r = i / 2 + i % 2;//这样能够把长度为奇数和偶数的两种情况统一起来。 while (l >= 0 && r < n && s[l] == s[r]) { --l; ++r; ++ans; } }还有没有优化的空间呢?让我们看看在中心拓展法中出现的两个问题,然后了解一下马拉车算法如何对这两个问题进行处理。 1. 长回文串中的重复查找(关键):为了更简单直接地说明问题,我举一个极端的特例:字符串s="aaaaaaa",并先对奇回文子串进行查找。尽管我们在以第2位字符为对称中心左右扩展时能够发现左回文子串s1="aaa",并且以第四位字符为对称中心左右扩展能够发现了长回文串s,那么之后的查找中是否仍需要匹配后三位字符串呢?设Im为长回文串的对称中心
其实,我们可以发现,若在一个长回文串中发现了左回文子串,根据回文串的对称性,那么在一定区域内的右子串中必然也存在一个回文串。因此,上述重复查找过程是可以省去的。 2.对长度奇数或偶数的回文子串分情况讨论马拉车算法: 一、算法分析: 马拉车算法的核心思路就在于,对每个长回文串的对称中心向两边进行拓展,同时记下前面已经查找过的回文子串半径(原理是动态规划的思想),其本质在于,如果能够找到一个长回文串,同时在它的对称中心左区域中找到一个回文子串,由于回文串的对称性,其右区域中必然是同样的回文子串。因此这个算法能快速地找出最长的回文子串。当然也能用来求解回文子串的个数。 二、算法实现: 1.预处理(解决了奇偶回文串问题): 为了利用回文串的对称性,同时解决回文子串长度有奇数和偶数两种情况的问题,马拉车算法在字符串首尾及每个字符间都插入一个 "#"。可以发现,无论回文子串原来是奇数还是偶数,最终都会变成奇回文子串,因此能够统一处理。即令原字符串为s,预处理后有 ts = s.replace('', '#') 我们定义①当前向两边拓展距离最大的回文串为最大回文串,即一个长回文串;②从对称中心到左端点的距离为最大回文半径,并假设为d;当我们求出最大回文半径d时,最大回文串的长度正好是d。
另外,在下面的步骤中,为了避免数组越界,我们还要在字符串开头加一个"$",结尾加一个"!",这样开头和结尾的两个字符一定不相等,循环就可以在这里终止。
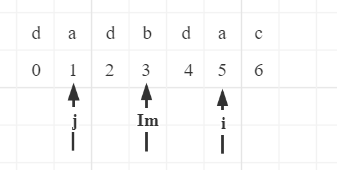
预处理代码如下 s = '$' + input().replace('', '#') + '!' #为了避免数组越界,让开头和结尾的两个字符一定不相等,循环就可以在这里终止。2.初始化(解决了重复查找问题): 数据结构与逻辑变量:马拉车算法的要求维护的变量有,一个数组d[]记录最大回文半径,d[i]表示以第i位元素为对称中心的最大回文半径,初始化长度为0(半径算上中心就是1);当前最大回文串的(即长回文串)对称中心Im及其右端点r,初始化皆为0。初始化: 以字符串"dadbdac"为例
这里有两种情况: Case 1: ir-i时,通过d加速拓展的右子串超出了长回文串的范围。然而大于右端点的回文串我们还没有开始匹配,此时d[i] = r - i . 比方说,当Im=3时,有r=5;当i=5时,有j=1,并且前面已经算出d[j] = 1。此时d[j]>r-i,向右拓展超出了长回文串范围,则d[i]应为i到右端点r的距离,即r-i。因此,当对称中心i被包含在当前最大回文串内时,有 d[i]=min(d[2 * Im - i],r - i) (核心:如果d[j]+ir,此时用常规的中心拓展法更新d[]、Im以及r。 3.中心拓展: 经过了上面的初始化,我们每次枚举对称中心的时候就都能够保证 s[i-d[i]]=s[i+d[i]],而现在,只要再满足ts[i - d[i]-1]==ts[i + d[i]+1],则不断向左右两边拓展半径。 综上所述,我们能够写出马拉车算法的核心代码: for i in range(2, len(s)-2): if(ir的情况),计算出d[i]=5,则此时容易得到r=i+d[i]=13,同时更新Im=8。对于ir,说明当前对称中心i拓展出了回文串,于是此时需要更新对称中心Im为i,右端点r为i+d[i]。而对于i>r的情况,由于d[i]总是等于0,此时更新Im=i,r=i;即 if (i + d[i] > r): Im, r = i, i + d[i]顺带提一句,最开始我以为马拉车这个算法名字应该是根据Manacher英译而来,但是这个中心扩展的思路,加上通过d[i]记录了最大回文串的半径避免了重复匹配,光看这两行代码: while (s[i - d[i] - 1] == s[i + d[i] + 1]) d[i]++; if (i + d[i] > r){Im=i, r = i + d[i];}真是有两头马在拉着一个对称中心向两边跑的感觉,大概就像这样: 然后不断更新最大回文串的对称中心Im和 r,通过d[i] = min(d[2 * Im - i], r - i)快速求解 如何求解ans就不解释啦,直接上代码: s = '$' + input().replace('', '#') + '!' d,Im,r,ans= [0]*(len(s)-2),0,0,0 for i in range(1, len(s)-2): if (i ma) else (ma,ans) print(ans.replace('#',''))
|
【本文地址】
今日新闻 |
推荐新闻 |