现代控制理论(4) |
您所在的位置:网站首页 › 非线性系统的概念 › 现代控制理论(4) |
现代控制理论(4)
|
文章目录
一、李雅普诺夫关于稳定性的定义1.李氏意义下的稳定2.渐近稳定3.大范围渐近稳定4.不稳定
二、李雅普诺夫第一法1.线性系统的稳定判据2.非线性系统的稳定判据
三、李雅普诺夫第二法1.标量函数的定号性2.稳定性原理
四、李雅普诺夫方法在线性系统中的应用五、李雅普诺夫方法在非线性系统中的应用1.雅可比矩阵法2.变量梯度法
一、李雅普诺夫关于稳定性的定义
系统 x ˙ = f ( x , t ) \dot x=f(x,t) x˙=f(x,t),若存在状态 x e x_e xe满足 x ˙ e ≡ 0 \dot x_e\equiv 0 x˙e≡0,则该状态为平衡状态 1.李氏意义下的稳定系统对于任意选定的实数
ε
>
0
\varepsilon>0
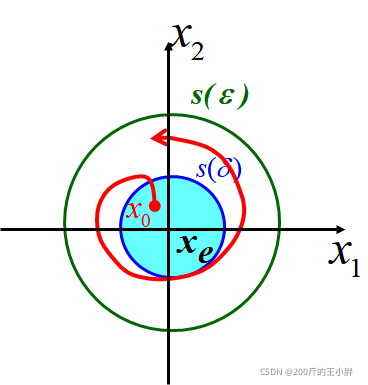
ε>0,都存在一个实数
δ
>
0
\delta>0
δ>0,当满足
∣
∣
x
0
−
x
e
∣
∣
≤
δ
||x_0-x_e||\leq\delta
∣∣x0−xe∣∣≤δ 从任意
x
0
x_0
x0出发的解都满足
∣
∣
Φ
−
x
e
∣
∣
≤
ε
||\Phi-x_e||\leq\varepsilon
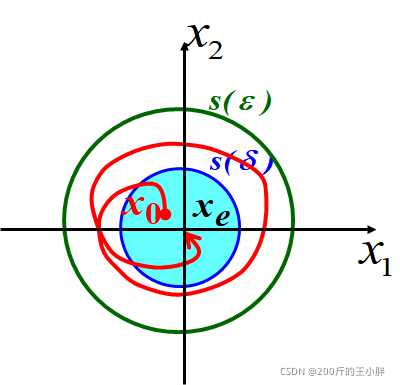
∣∣Φ−xe∣∣≤ε 则称平衡状态为李氏意义下的稳定 解最终收敛于
x
e
x_e
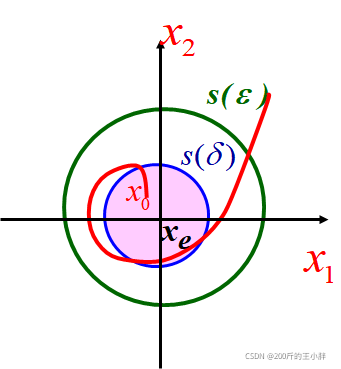
xe 从状态空间中所有初始状态出发的轨线都具有渐近稳定性,称这种平衡状态 x e x_e xe为大范围内渐近稳定 4.不稳定不管
δ
\delta
δ有多小,只要由
S
(
δ
)
S(\delta)
S(δ)内出发的状态轨迹超出
S
(
ε
)
S(\varepsilon)
S(ε) 以外,则称此平衡状态是不稳定的 李氏稳定(状态稳定)的充要条件:系统矩阵A的全部特征值位于复平面的左半部 输出稳定的充要条件:传递函数 W ( s ) = C ( S I − A ) − 1 B W(s)=C(SI-A)^{-1}B W(s)=C(SI−A)−1B的全部极点位于复平面左半部 PS:输出稳定不一定状态稳定,可能存在零极点对消 2.非线性系统的稳定判据非线性系统状态方程
x
˙
=
f
(
x
)
\dot x=f(x)
x˙=f(x)
f
(
x
)
=
[
f
1
,
f
2
⋯
f
n
]
f(x)=[f_1,f_2\cdots f_n]
f(x)=[f1,f2⋯fn] 向量函数的雅可比矩阵: V ( x ) V(x) V(x)为x所定义的标量函数,对于任何非零矢量x,如果: 1) V ( x ) > 0 V(x)>0 V(x)>0,则为正定的 2) V ( x ) ≥ 0 V(x)\geq0 V(x)≥0,则为半正定的 3) V ( x ) < 0 V(x) ∞ ||x||->\infty,V(x)->\infty ∣∣x∣∣−>∞,V(x)−>∞,则系统是大范围渐近稳定的 2、 V ( x ) V(x) V(x)正定, V ˙ ( x ) \dot V(x) V˙(x)半负定,在非零状态 V ˙ ( x ) \dot V(x) V˙(x) 不恒为 0,在原点是渐近稳定的 3、 V ( x ) V(x) V(x)正定, V ˙ ( x ) \dot V(x) V˙(x)半负定,在非零状态 V ˙ ( x ) \dot V(x) V˙(x) 恒为 0,在原点是李氏意义下的稳定 4、 V ( x ) V(x) V(x)正定, V ˙ ( x ) \dot V(x) V˙(x)正定,在原点是不稳定的 5、 V ( x ) V(x) V(x)正定, V ˙ ( x ) \dot V(x) V˙(x)正半定,在非零状态 V ˙ ( x ) \dot V(x) V˙(x) 不恒为 0,在原点是不稳定的 6、 V ( x ) V(x) V(x)正定, V ˙ ( x ) \dot V(x) V˙(x)正半定,在非零状态 V ˙ ( x ) \dot V(x) V˙(x) 恒为 0,在原点是李氏意义下的稳定 四、李雅普诺夫方法在线性系统中的应用选定正定二次型函数 V ( x ) V(x) V(x)为李氏函数 V ( x ) = x T P x V(x)=x^TPx V(x)=xTPx V ˙ ( x ) = x T ( P A + A T P ) x \dot V(x)=x^T(PA+A^TP)x V˙(x)=xT(PA+ATP)x 令 Q = − ( P A + A T P ) Q=-(PA+A^TP) Q=−(PA+ATP) 如果Q正定,则系统是大范围渐进稳定的 判定稳定性的步骤: 1、选取正定矩阵Q(通常是单位阵) 2、由 Q = − ( P A + A T P ) Q=-(PA+A^TP) Q=−(PA+ATP)求P 3、判断P的正定性 4、稳定性结论 五、李雅普诺夫方法在非线性系统中的应用 1.雅可比矩阵法
x
˙
=
f
(
x
)
\dot x=f(x)
x˙=f(x) 判定稳定性的步骤: 1、求雅可比矩阵 1、设
∇
V
=
\nabla V=
∇V= |
【本文地址】
今日新闻 |
推荐新闻 |
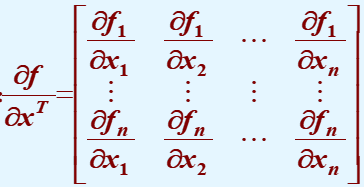 原非线性状态方程化为线性状态方程
Δ
x
˙
=
∂
f
∂
x
T
Δ
x
\Delta\dot x=\frac{\partial f}{\partial x^T}\Delta x
Δx˙=∂xT∂fΔx 其中
Δ
x
=
x
−
x
e
\Delta x=x-x_e
Δx=x−xe 然后可套用线性系统的稳定判据
原非线性状态方程化为线性状态方程
Δ
x
˙
=
∂
f
∂
x
T
Δ
x
\Delta\dot x=\frac{\partial f}{\partial x^T}\Delta x
Δx˙=∂xT∂fΔx 其中
Δ
x
=
x
−
x
e
\Delta x=x-x_e
Δx=x−xe 然后可套用线性系统的稳定判据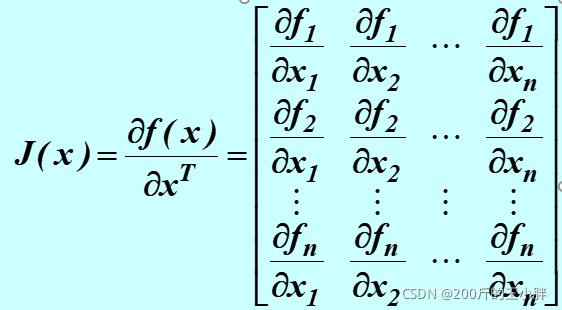 2、克拉索夫斯基表达式:
Q
(
x
)
=
−
[
J
T
+
J
]
Q(x)=-[J^T+J]
Q(x)=−[JT+J] 3、判断Q的正定性 4、稳定性结论 PS:克拉索夫斯基定理只是渐近稳定的一个充分条件不是必要条件
2、克拉索夫斯基表达式:
Q
(
x
)
=
−
[
J
T
+
J
]
Q(x)=-[J^T+J]
Q(x)=−[JT+J] 3、判断Q的正定性 4、稳定性结论 PS:克拉索夫斯基定理只是渐近稳定的一个充分条件不是必要条件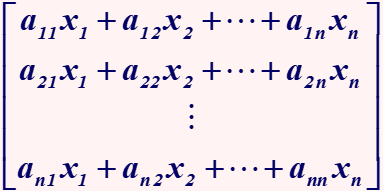 2、
V
˙
(
x
)
=
(
∇
V
)
T
x
˙
\dot V(x)=(\nabla V)^T\dot x
V˙(x)=(∇V)Tx˙ 限定
V
˙
(
x
)
\dot V(x)
V˙(x)为负定 3、利用
n
(
n
−
1
)
2
\frac{n(n-1)}{2}
2n(n−1)个旋度方程确定
∇
V
\nabla V
∇V中的未知数
2、
V
˙
(
x
)
=
(
∇
V
)
T
x
˙
\dot V(x)=(\nabla V)^T\dot x
V˙(x)=(∇V)Tx˙ 限定
V
˙
(
x
)
\dot V(x)
V˙(x)为负定 3、利用
n
(
n
−
1
)
2
\frac{n(n-1)}{2}
2n(n−1)个旋度方程确定
∇
V
\nabla V
∇V中的未知数 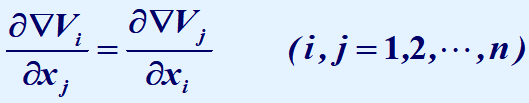 4、计算并验证V正定性
4、计算并验证V正定性 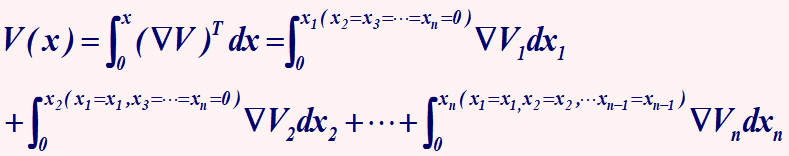 5、确定系统渐进稳定的范围
5、确定系统渐进稳定的范围