（从零开始）基于检测前跟踪雷达目标跟踪技术的研究：第（2）周所学知识（02） |
您所在的位置：网站首页 › 雷达目标检测算法 › （从零开始）基于检测前跟踪雷达目标跟踪技术的研究：第（2）周所学知识（02） |
（从零开始）基于检测前跟踪雷达目标跟踪技术的研究：第（2）周所学知识（02）
|
若由本篇博文增加关注，就解封本篇博文的VIP权限哈，记得在下方留言哈 本篇文章将开始进行DP-TBD。首先你需要了解什么是DP即动态规划，而不是急于去找什么是DP-TBD。动态规划是一种最优化的思想，DP-TBD是在这种思想上发展起来的。 为了能够深入了解什么是动态规划，你首先必须要掌握以下三点： Viterbi（维特比）算法多阶段决策HMM 这三点你必须要好好百度一下看看相关知识，这对于下面了解动态规划很重要！很重要！很重要！ 有了上面的知识后，咱们来看一下一个最短路径问题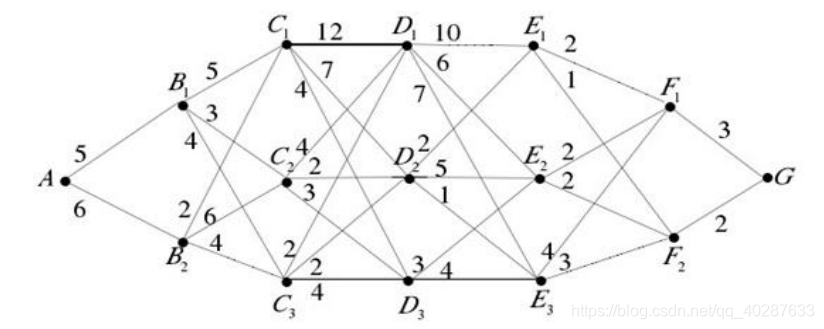 如果要求从A到G的最短路径，最简单的方法就是把从A到G的所有路径全部找出来，然后把各条路径上的权值相加找到最小值所对应的路径即可。但是当路径很复杂的时候就会出现，用上面的穷举法会特别麻烦。所以就出现了一种叫做动态规划的思想。 对于上图我需要有以下几点说明：
A,B1,B2…F1,F2,G：所处的状态，称为状态变量A:第一阶段，B1,B2：第二阶段，后面的以此类推只有相邻的两个阶段有路径，有间隔的阶段可没有路径的。从当前时刻的一个状态到下一个阶段的状态（下一个阶段的哪个状态都有可能）：决策路径上的权值：决策代价从A到G的每一条路径的长度即权值之和：整体代价，其实我们如果在找最短路径的话，就是找这个整体代价的最小值。如果要找最优路径，不论到达哪一阶段的哪个状态变量，剩下的肯定还是找最优路径。
接下来我要抛出很多的变量了，仔细阅读，自己在纸上跟着我的思路画一下，你会更加理解下面变量的意思：
xk:k：是第k阶段，xk则是第k阶段的状态变量uk(xk):k阶段时的决策，称为决策变量Uk(xk):uk(xk)的集合策略：从开始到最后阶段所做的决策的集合即： {u1(x1)，u2(x2)，u3(x3),…,uk(xk)}值函数：这个函数很重要，怎样找到最优路径，就是看这个值函数什么时候达到最大，它用来评价整体代价的优劣。即： v(x1;u1,u2,…uk)fk(xk)=max v(x1;u1,u2,…uk):最优值函数wj(xj,uj):决策代价，可以类比上图中的权值
假设
v
(
x
1
;
u
1
,
u
2
,
⋯
,
u
k
)
=
∑
j
=
1
k
w
j
(
x
j
,
u
j
)
v\left(x_{1} ; u_{1}, u_{2}, \cdots,u_{k}\right)=\sum_{j=1}^{k} w_{j}\left(x_{j}, u_{j}\right)
v(x1;u1,u2,⋯,uk)=∑j=1kwj(xj,uj) 可以认为此处的值函数是一条路径上的权值之和此时
f
k
(
x
k
)
=
max
{
u
,
j
∈
U
[
∑
j
=
1
k
w
j
(
x
j
,
u
j
)
]
=
max
(
u
j
,
v
k
)
∈
U
[
w
k
(
x
k
,
u
k
)
+
∑
j
=
1
k
−
1
w
j
(
x
j
,
u
j
)
]
=
max
{
u
k
}
∈
U
[
w
k
(
x
k
,
u
k
)
+
f
k
−
1
(
x
k
−
1
)
]
,
k
=
2
,
3
,
⋯
,
M
\begin{aligned} f_{k}\left(x_{k}\right) &=\max _{\{u, j \in U}\left[\sum_{j=1}^{k} w_{j}\left(x_{j}, u_{j}\right)\right] \\ &=\max _{\left(u_{j}, v_{k}\right) \in U}\left[w_{k}\left(x_{k}, u_{k}\right)+\sum_{j=1}^{k-1} w_{j}\left(x_{j}, u_{j}\right)\right] \\ &=\max _{\left\{u_{k}\right\} \in U}\left[w_{k}\left(x_{k}, u_{k}\right)+f_{k-1}\left(x_{k-1}\right)\right], \quad k=2,3, \cdots, M \end{aligned}
fk(xk)={u,j∈Umax[j=1∑kwj(xj,uj)]=(uj,vk)∈Umax[wk(xk,uk)+j=1∑k−1wj(xj,uj)]={uk}∈Umax[wk(xk,uk)+fk−1(xk−1)],k=2,3,⋯,M（1）我们假设初始的决策代价是
f
1
(
x
1
)
=
w
1
(
x
1
,
u
1
)
f_{1}\left(x_{1}\right)=w_{1}\left(x_{1}, u_{1}\right)
f1(x1)=w1(x1,u1)（2）由式（1）和式（2）可得
f
k
(
x
k
)
=
max
{
u
k
}
∈
U
[
w
k
(
x
k
,
u
k
)
+
f
k
−
1
(
x
k
−
1
)
]
f_{k}\left(x_{k}\right)=\max _{\left\{u_{k}\right\} \in U}\left[w_{k}\left(x_{k}, u_{k}\right)+f_{k-1}\left(x_{k-1}\right)\right]
fk(xk)=max{uk}∈U[wk(xk,uk)+fk−1(xk−1)]
=
max
{
u
k
}
∈
U
{
w
k
(
x
k
,
u
k
)
+
max
{
u
k
−
1
}
∈
U
[
w
k
−
1
(
x
k
−
1
,
u
k
−
1
)
]
+
…
+
max
{
u
2
}
∈
U
[
w
2
(
x
2
,
u
2
)
]
+
f
1
(
x
1
)
}
=\max _{\left\{u_{k}\right\} \in U}\left\{w_{k}\left(x_{k}, u_{k}\right)+\max _{\left\{u_{k-1}\right\} \in U}\left[w_{k-1}\left(x_{k-1}, u_{k-1}\right)\right]+\ldots+\max _{\left\{u_{2}\right\} \in U}\left[w_{2}\left(x_{2}, u_{2}\right)\right]+f_{1}\left(x_{1}\right)\right\}
=max{uk}∈U{wk(xk,uk)+max{uk−1}∈U[wk−1(xk−1,uk−1)]+…+max{u2}∈U[w2(x2,u2)]+f1(x1)}
=
max
{
u
k
}
∈
U
[
h
k
(
x
k
)
]
=\max _{\left\{u_{k}\right\} \in U}\left[h_{k}\left(x_{k}\right)\right]
=max{uk}∈U[hk(xk)]
h
k
(
x
k
)
=
w
k
(
x
k
,
u
k
)
+
max
{
u
k
−
1
}
∈
U
[
h
k
−
1
(
x
k
−
1
)
]
h_{k}\left(x_{k}\right)=w_{k}\left(x_{k}, u_{k}\right)+\max _{\left\{u_{k-1}\right\} \in U}\left[h_{k-1}\left(x_{k-1}\right)\right]
hk(xk)=wk(xk,uk)+max{uk−1}∈U[hk−1(xk−1)]我们称hk(xk)为阶段值函数，这里的阶段值函数该怎样理解呢？v(x1;u1,u2,…uk)是一条完整路径上的值函数，而阶段值函数，顾名思义，它是前k阶段的值函数，这就是每一阶段都有一个值函数，当然这个值函数是根据wk(xk,uk)的取值不同而随之变化的。我们假设
h
1
(
x
1
)
=
w
1
(
x
1
,
u
1
)
h_{1}\left(x_{1}\right)=w_{1}\left(x_{1}, u_{1}\right)
h1(x1)=w1(x1,u1)接下来就到最重要的一步了，最优策略：
{
x
^
K
}
=
{
x
^
K
:
(
∑
k
=
1
K
h
k
(
x
k
)
)
max
}
\left\{\hat{x}_{K}\right\}=\left\{\hat{x}_{K}:\left(\sum_{k=1}^{K} h_{k}\left(x_{k}\right)\right)_{\max }\right\}
{x^K}={x^K:(∑k=1Khk(xk))max}其中
x
^
K
=
{
x
^
(
1
)
,
x
^
(
2
)
,
⋯
,
x
^
(
K
)
}
\hat{x}_{K}=\{\hat{x}(1), \hat{x}(2), \cdots, \hat{x}(K)\}
x^K={x^(1),x^(2),⋯,x^(K)}，这里记录了最优策略中每一阶段决策时对应的状态。
|
【本文地址】
今日新闻 |
推荐新闻 |